Курсовая ТОКБ. Курсовая_ТОКБ. Разработка модели управления процессом обеспечения информационной безопасности на примере электронной подписи
 Скачать 1.08 Mb. Скачать 1.08 Mb.
|
3.2 О возможностях сетевого моделированияСетевое моделирование позволяет решать отдельные задачи при задании небольшого количества сочетаний исследуемых параметров системы. Основными параметрами сетевого графика являются: 1) Наиболее раннее возможное время наступления j-го события Тp (j), вычисляемое по формуле:  (3.1) (3.1)где символами i и j обозначаются номера предшествующего и последующего событий соответственно; -tij — продолжительность (i, j) -й работы. Из обозначения 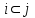 следует, что событие i предшествует событию j. следует, что событие i предшествует событию j.2) Самое позднее допустимое время наступления i-го события Тп (i), вычисляемое по формуле  (3.2) (3.2)где из обозначения 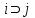 следует, что событие j предшествует событию i следует, что событие j предшествует событию i3) Резерв времени данного события Ri, вычисляемый по формуле 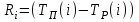 (3.3) (3.3)4) Полный резерв времени работы rп (i,j), вычисляемый по формуле 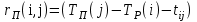 (3.4) (3.4)Смысл полного резерва времени работы заключается в том, что задержка в выполнении работы (i,j) на величину ∆tij ≥ rп (i,j), приводит к задержке в наступлении завершающего события на величину (∆tij - rп (i,j)). 5) Свободный резерв времени работы rc (i,j), вычисляемый по формуле 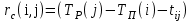 (3.5) (3.5)Смысл свободного резерва времени работы заключается в том, что задержка в выполнении работы на величину ∆tij≤rC(i,j) не влияет ни на один другой срок, определенный данным сетевым графиком. Основными показателями сетевого графика, по которым выполняется его анализ, являются: 1) Критический путь — это полный путь, на котором суммарная продолжительность работ является максимальной. Иными словами, это самый длинный по времени путь в сетевом графике от исходного до завершающего события. Критический путь лимитирует выполнение операции, поэтому любая задержка на работах критического пути увеличивает время всего процесса. События, через которые проходит критический путь, и работы, лежащие на критических путях, называются напряженными. У критических работ как полные, так и свободные резервы времени равны нулю (признак критической работы). Критический путь рассчитывается путем определения работ, полные резервы времени которых равны нулю. 2) Полный резерв времени ненапряженного пути — это резерв времени ненапряженных событий и работ, т. е. тех, которые лежат не на критическом пути. В том случае, если ненапряженный и критический пути не пересекаются, полный резерв времени ненапряженного пути равен разности между его длиной и длиной критического пути (во временной мере). Если ненапряженный и критический пути пересекаются, полный резерв времени равен самому длительному участку ненапряженного пути, заключенному между соответствующими парами событий критического пути. Полный резерв времени ненапряженного пути показывает, на сколько в сумме может быть увеличена продолжительность всех работ этого пути без изменения срока выполнения операции в целом. Сущность анализа сетевого графика заключается в том, что выявляются резервы времени работ, лежащих на ненапряженных путях, и направляются на работы, лежащие на критическом пути, который лимитирует срок завершения работы в целом. Этим достигается сокращение времени выполнения критических работ, а значит, и всей операции. 3) Время выполнения работ (временные оценки работ) может определяться либо по нормативам (статистическим показателям), либо при отсутствии их — по следующим эмпирическим формулам: 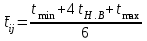 (3.6) (3.6)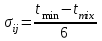 (3.7) (3.7)где 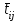 — математическое ожидание продолжительности выполнения (i,j) работы (среднеожидаемое время работы); — математическое ожидание продолжительности выполнения (i,j) работы (среднеожидаемое время работы);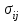 — среднеквадратическая ошибка в определении продолжительности работы; — среднеквадратическая ошибка в определении продолжительности работы;tmin — продолжительность работы в наиболее благоприятных условиях (оптимистическая оценка); tmax — продолжительность работы при самом неблагоприятном стечении обстоятельств (пессимистическая оценка); tH.B — продолжительность работы при условии, что не возникает никаких неожиданных трудностей (наиболее вероятная оценка). Математическое ожидание любого параметра сетевого графика, являющегося суммой величин tij равно 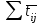 Среднеквадратическая ошибка в определении этого параметра равна 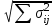 . .Вероятность свершения j –го события в расчётный срок рjопределяется по формуле 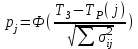 где Ф(…) — функция Лапласа; TЗ — заданный срок свершения события; TР(j) — время раннего свершения j-го события; 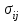 - среднеквадратические ошибки в определении продолжительности работ, которые использовались при вычислении раннего срока наступления j-го события. - среднеквадратические ошибки в определении продолжительности работ, которые использовались при вычислении раннего срока наступления j-го события.Технология управления процессом обеспечения ИБ Основные угрозы, способные повлиять на работоспособность системы, изображены на рисунке 8. Исходя из этого, можем составить план мониторинга системы. 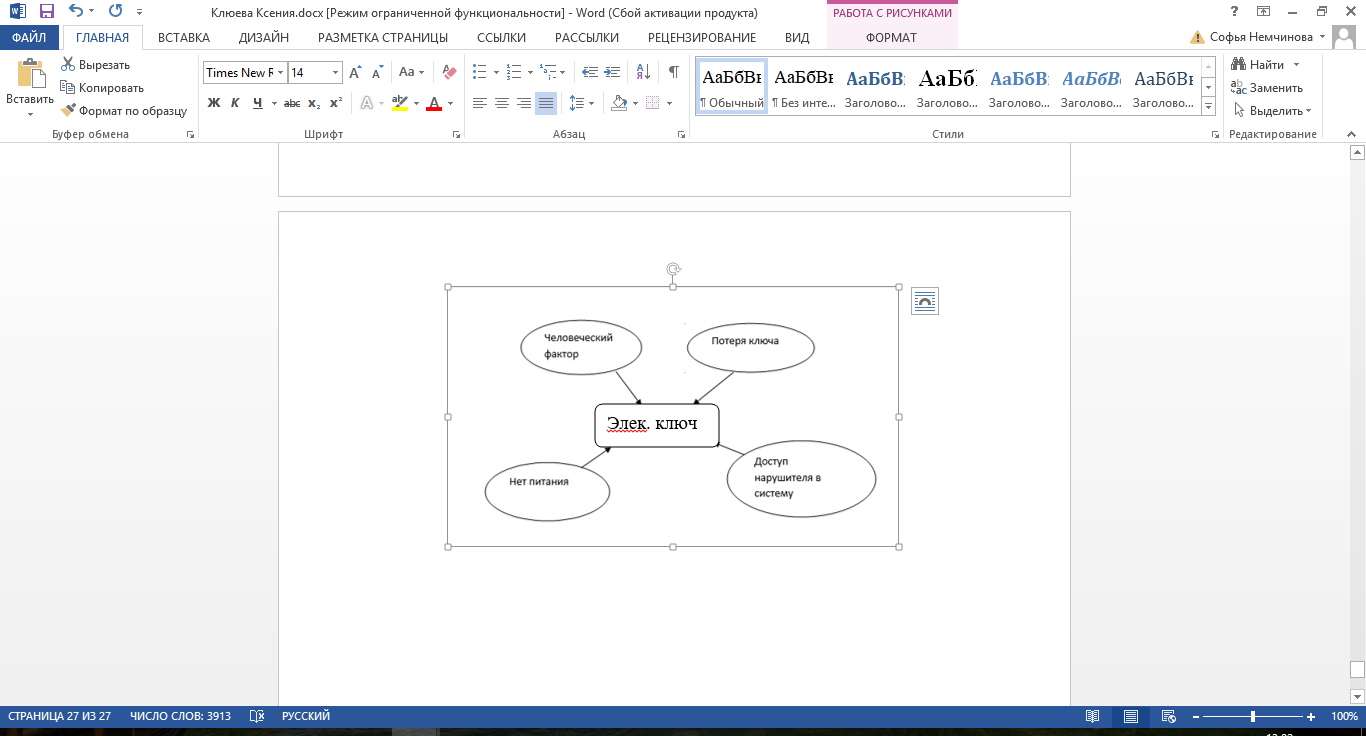 Рисунок 13. Основные угрозы Для составления сетевой модели мониторинга системы нужно определить список работ, которые следует сделать для полного мониторинга и время, потраченное на эти работы (Таблица 1). 4.1 Разработка сетевой модели формирования угрозы  Рисунок 14. Сетевая модель формирования угрозы
Таблица 1. Перечень угроз 4.2 Разработка сетевой модели устранения проблемы Определяем работы, которые следует сделать для полного устранения выявленных проблем: 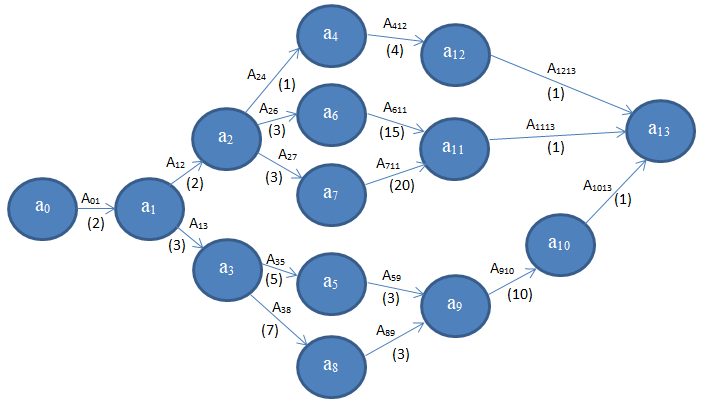 Рисунок 15. Сетевая модель устранения проблемы
Таблица 2. Перечень работ устранения проблем в системе 4.3 Анализ сетевого графика устранения проблемы Наиболее раннее возможное время наступления j-го события 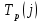 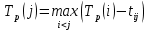
Самое позднее допустимое время наступления i-го события Тп(i). 
Резерв времени данного события 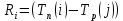
Полный резерв времени каждой работы. 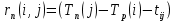
|
