Курсовой по цифровой схемотехнике. Курсовой проект Слёзкин (1). Разработка схемной реализации цифрового устройства с временным разделением сигналов с входными параметрами F1 (0,2,4,6,8,10) F2 (1,3,5,7) Fбн (11,12,13) такты F1 (24) такты F2 (79) Ксч 10 Fгни 4,0 кГц
 Скачать 2.94 Mb.
|
РАЗРАБОТКА ФУНКЦИОНАЛЬНОЙ СХЕМЫ ПРОЕКТИРУЕМОГО УСТРОЙСТВА2.1 Изучение методов минимизаций логических функцийКарты Карно Графический способ минимизации булевых функций. Представляет собой операции попарного неполного склеивания и элементарного поглощения. Карты Карно рассматриваются как построенная соответствующим образом таблица истинности функции. Карты Карно можно рассматривать как определенную плоскую развертку n-мерного булева куба. Карты Карно были изобретены в 1952 Эдвардом В. Вейчем и усовершенствованы в 1953 Морисом Карно, физиком из «Bell Labs», и были призваны помочь упростить цифровые электронные схемы. В карту Карно булевы переменные передаются из таблицы истинности и упорядочиваются с помощью кода Грея, в котором каждое следующее число отличается от предыдущего только одним разрядом. Булевы функции переменных, представленные в виде СДНФ или СКНФ, могут иметь в своём составе различных элементарных членов. Основным методом минимизации логических функций, представленных в виде СДНФ или СКНФ, является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной.  Таким образом, главной задачей при минимизации СДНФ и СКНФ является поиск термов, пригодных к склейке с последующим поглощением, что для больших форм может оказаться достаточно сложной задачей. Карты Карно предоставляют наглядный способ отыскания таких термов.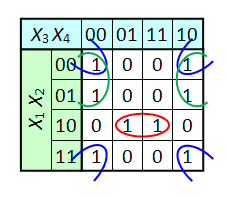 Рис. 1. Пример Карт Карно  Метод минимизации Квайна и Мак-Класки.На практике область применения рассмотренных ранее методов минимизации логических функций с использованием карт Карно или Вейча ограничивается числом логических переменных не более пяти. Это объясняется двумя основными причинами: – при увеличении числа переменных метод теряет свою наглядность, что снижает эффективность его применения; – так как выбор покрытий производится по большей части интуитивно, то конечный результат минимизации сильно зависит от индивидуального опыта разработчика. Последнее препятствует применению для минимизации ЭВМ. При увеличении числа переменных для минимизации логических функций используются методы, обладающие однозначностью алгоритма, что является предпосылкой применения ЭВМ. К таким методам относятся метод Квайна и Мак-Класки . Этот метод содержит два этапа преобразования выражения функции: на первом этапе осуществляется переход от канонической формы (СДНФ или СКНФ) к так называемой сокращенной форме, на втором этапе – переход от сокращенной формы логического выражения к минимальной форме. 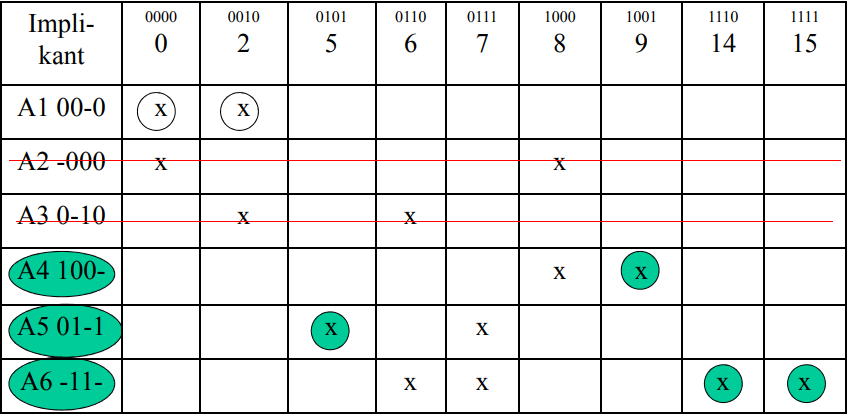 Рис. 2. Пример применения метода минимизации Квайна и Мак-Класки Метод Блейка-Порецкого Метод Блейка – Порецкого основывается на утверждении: если в произвольной ДНФ минимизируемой ПФ произвести все возможные обобщенные склеивания и все возможные поглощения, то в результате будет получена сокращенная ДНФ исходной функции.  Методы Квайна и Блейка-Порецкого являются аналитическими. В этих методах наиболее трудоемким является процесс отыскания склеивающихся между собой конъюнкций. Существуют методы, которые позволяют упростить поиск склеивающихся членов. Один из наиболее удобных методов минимизации ПФ от небольшого числа переменных основан на использовании диаграмм Вейча или карт Карно. Диаграмма Вейча представляет собой фактически таблицу истинности ПФ, которая представляется не в виде столбцов, а в виде специальных карт. Каждой клетке диаграммы соответствует определенный набор значений аргументов. Поэтому диаграммы можно рассматривать как графическое представление совокупности всех конституэнт единицы. При этом диаграмма строится таким образом, что склеивающиеся между собой конституэнты оказываются расположенными в соседних клетках, т.к. отличаются значением только одной переменной. Приведем примеры построения диаграммы Вейча и карт Карно для ПФ от разного числа аргументов.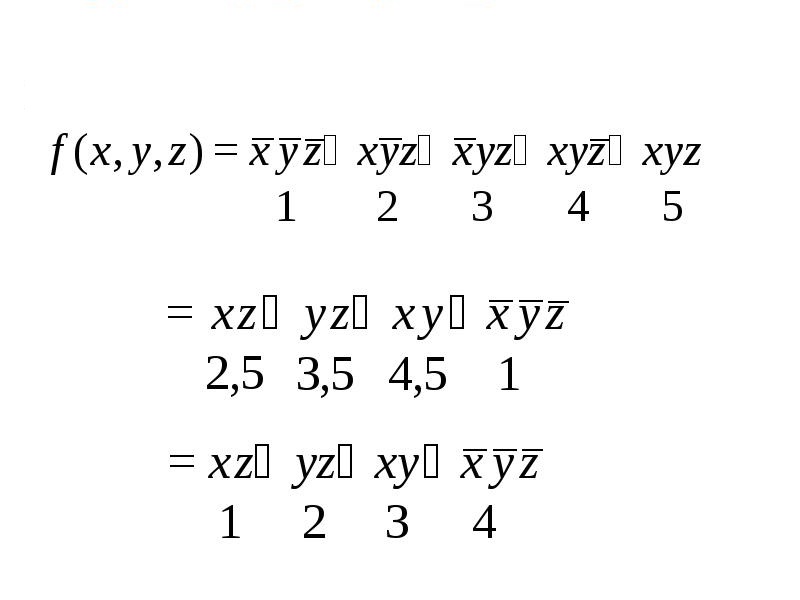 Рис. 3. Метод Блейка-Порецкого  |