Минимизация функции 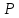 алгоритмом Квайна-МакКласке: алгоритмом Квайна-МакКласке:
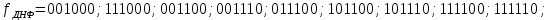 001001; 111001; 000001; 000011; 000101; 000111; 001011; 001101; 001111; 010001; 010001; 010101; 010111; 011011; 0111101; 011101; 011111; 100001; 100011; 100101; 100111; 101011; 101101; 101111; 110001; 110011; 110101; 110111; 111011; 111101; 111111. 001001; 111001; 000001; 000011; 000101; 000111; 001011; 001101; 001111; 010001; 010001; 010101; 010111; 011011; 0111101; 011101; 011111; 100001; 100011; 100101; 100111; 101011; 101101; 101111; 110001; 110011; 110101; 110111; 111011; 111101; 111111.
  C1 C1
|
|
000001
|
1)─
|
|
C3
|
|
110001
|
19) ─
|
|
C5
|
|
111011
|
37) ─
|
|
001000
|
2) ─
|
|
|
111000
|
20) ─
|
|
|
111101
|
38) ─
|
 C2 C2
|
|
000011
|
3) ─
|
|
 C4 C4
|
|
001111
|
21) ─
|
|
|
111110
|
39) ─
|
|
000101
|
4) ─
|
|
|
010111
|
22) ─
|
|
C6
|
111111
|
40) ─
|
|
001001
|
5) ─
|
|
|
011011
|
23) ─
|
|
|
|
|
|
|
001100
|
6) ─
|
|
|
011101
|
24) ─
|
|
|
|
|
|
|
010001
|
7) ─
|
|
|
011110
|
25) ─
|
|
|
|
|
|
|
100001
|
8) ─
|
|
|
100111
|
26) ─
|
|
|
|
|
|
C3
|
|
000111
|
9) ─
|
|
|
101011
|
27) ─
|
|
|
|
|
|
|
001011
|
10) ─
|
|
|
101101
|
28) ─
|
|
|
|
|
|
|
001101
|
11) ─
|
|
|
101110
|
29) ─
|
|
|
|
|
|
|
001110
|
12) ─
|
|
|
110011
|
30) ─
|
|
|
|
|
|
|
010011
|
13) ─
|
|
|
110101
|
31) ─
|
|
|
|
|
|
|
010101
|
14) ─
|
|
|
111001
|
32) ─
|
|
|
|
|
|
|
011100
|
15) ─
|
|
|
111100
|
33) ─
|
|
|
|
|
|
|
100011
|
16) ─
|
|
C5
|
|
011111
|
34) ─
|
|
|
|
|
|
|
100101
|
17) ─
|
|
|
101111
|
35) ─
|
|
|
|
|
|
|
101100
|
18) ─
|
|
|
110111
|
36) ─
|
|
|
|
|
|
C1
|
|
0000X1
|
1)─
|
|
|
|
X10011
|
42) ─
|
|
|
|
11X101
|
83) ─
|
|
000X01
|
2) ─
|
|
C3
|
|
0101X1
|
43) ─
|
|
C4
|
|
1110X1
|
84) ─
|
|
00X001
|
3) ─
|
|
|
01X101
|
44) ─
|
|
|
111X01
|
85) ─
|
|
0X0001
|
4) ─
|
|
|
X10101
|
45) ─
|
|
|
11110X
|
86) ─
|
|
X00001
|
5) ─
|
|
|
01110X
|
46) ─
|
|
|
1111X0
|
87) ─
|
|
00100X
|
6) ─
|
|
|
0111X0
|
47) ─
|
|
|
|
X11111
|
88) ─
|
|
001X00
|
7) ─
|
|
|
X11100
|
48) ─
|
|
C5
|
|
1X1111
|
89) ─
|
C2
|
|
000X11
|
8) ─
|
|
|
100X11
|
49) ─
|
|
|
11X111
|
90) ─
|
|
00X011
|
9) ─
|
|
|
10X011
|
50) ─
|
|
|
111X11
|
91) ─
|
|
0X0011
|
10) ─
|
|
|
1X0011
|
51) ─
|
|
|
1111X1
|
92) ─
|
|
X00011
|
11) ─
|
|
|
1001X1
|
52) ─
|
|
|
11111X
|
93) ─
|
|
00X101
|
12) ─
|
|
|
10X101
|
53) ─
|
|
|
|
|
|
|
0001X1
|
13) ─
|
|
|
1X0101
|
54) ─
|
|
|
|
|
|
|
0X0101
|
14) ─
|
|
|
10110X
|
55) ─
|
|
|
|
|
|
|
X00101
|
15) ─
|
|
|
1011X0
|
56) ─
|
|
|
|
|
| |
 Скачать 401.88 Kb.
Скачать 401.88 Kb. алгоритмом Квайна-МакКласке:
алгоритмом Квайна-МакКласке: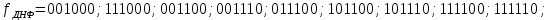 001001; 111001; 000001; 000011; 000101; 000111; 001011; 001101; 001111; 010001; 010001; 010101; 010111; 011011; 0111101; 011101; 011111; 100001; 100011; 100101; 100111; 101011; 101101; 101111; 110001; 110011; 110101; 110111; 111011; 111101; 111111.
001001; 111001; 000001; 000011; 000101; 000111; 001011; 001101; 001111; 010001; 010001; 010101; 010111; 011011; 0111101; 011101; 011111; 100001; 100011; 100101; 100111; 101011; 101101; 101111; 110001; 110011; 110101; 110111; 111011; 111101; 111111.
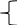
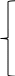 C1
C1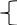
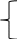
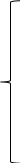
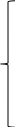 C2
C2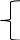 C4
C4