Разработка сумматора-умножителя. Курсовая работа (1). Разработка сумматораумножителя
 Скачать 401.88 Kb. Скачать 401.88 Kb.
|
|
Министерство образования Республики Беларусь Учреждение образования Белорусский государственный университет информатики и радиоэлектроники Кафедра электронных вычислительных машин Пояснительная записка к типовому расчету по дисциплине «Арифметические и логические основы вычислительной техники» Тема: Разработка сумматора-умножителя Выполнил: Германенко И.И. Студент гр. 480562 MRY Проверила: Лукьянова И.В. Минск 2015 Исходные данные: Исходные сомножители: 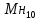 = 81,92; = 81,92; 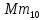 = 44,35; = 44,35;Алгоритм умножения: Г; Метод умножения: умножение закодированного двоично-четверичного множимого на 2 разряда двоичного множителя одновременно в прямых кодах; Варианты кодирования четверичных цифр двоичными кодами: 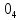 = 10; = 10; 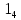 = 01; = 01; 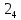 = 11; = 11; 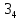 = 00; = 00;Тип синтезируемого умножителя: структурные схемы приведены для умножителя 2-го типа (ОЧС, ОЧУС, аккумулятор). Метод минимизации ОЧС: карты Карно-Вейча. Метод минимизации ОЧУС: Алгоритм Квайна-МакКласке, карты Карно-Вейча. Функционально полный логический базис для схемы ОЧС (А4): 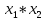 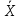 Логический базис для реализации ОЧС: 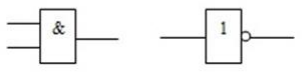 Функционально полный логический базис для схемы ОЧУС (А7): 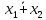 Логический базис для реализации ОЧУС: 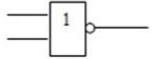 Арифметические операции сложения двоично-четверичных чисел с разными знаками в дополнительных кодах и умножения на 2 разряда множителя в прямых кодах должны выполняться одним цифровым устройством, именуемым сумматор-умножитель. Учитывая то, что суммирующие узлы обязательно входят в состав умножителя, начнем синтез с разработки алгоритма умножения. Разработка алгоритма умножения Перевод сомножителей из десятичной системы счисления в четверичную: Множимое:
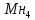 =1101,322 =1101,322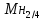 =01011001,001111 =01011001,001111Множитель:
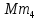 =230,112 =230,112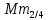 =110010,010111 =110010,010111Запишем сомножители в форме с плавающей запятой в прямом коде: Мн = 0,010110010011 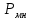 = 0.0110 (закодирован по заданию) = 0.0110 (закодирован по заданию)Мт = 0,01010001111010 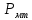 = 0.0011 (закодирован традиционно) = 0.0011 (закодирован традиционно)Умножение двух чисел с плавающей запятой на 2 разряда множителя одновременно в прямых кодах сводится к сложению порядков, формированию знака произведения, преобразованию разрядов множителя согласно алгоритму и перемножению мантисс сомножителей.
Результат закодирован в соответствии с заданием на кодировку множимого. Знак произведения определяется суммой по модулю двух знаков сомножителей: зн Мн  зн Мт = 0 + 0 = 0 зн Мт = 0 + 0 = 0Для умножения мантисс необходимо предварительно преобразовать множитель, чтобы исключить диаду 11 (34), заменив ее на триаду 1 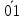 и диаду 10 (24). и диаду 10 (24).Преобразованный множитель имеет вид: 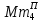 =1, =1,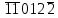 Мн = 0,110132 2Мн = 0,220330 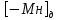 = 3,223202 = 3,223202 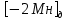 = 3,113010 = 3,113010Умножение по алгоритму Г
После окончания умножения необходимо оценить погрешность вычислений. Для этого полученное произведение 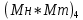 = 0,032023222110 приводится к нулевому порядку ( = 0,032023222110 приводится к нулевому порядку (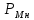 * *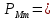 7), а затем переводится в десятичную систему счисления: 7), а затем переводится в десятичную систему счисления: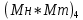 = 320232,22110 = 320232,22110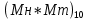 = 3630,64453125 = 3630,64453125Результат прямого перемножения операндов дает следующее значение: 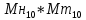 = 3633,15185547 = 3633,15185547Абсолютная погрешность: Δ = 3633,15185547 - 3630,64453125 = 2,50732422 δ 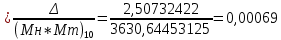 ; δ = ; δ = 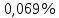 Эта погрешность получена за счет приближенного перевода из десятичной системы счисления в четверичную обоих сомножителей, а также за счет округления полученного результата произведения. Синтез структуры сумматора-умножителя 2го типа Структурная схема сумматора-умножителя 2го типа для алгоритма умножения “Г” приведена на рис.2. Если устройство работает как сумматор, то оба слагаемых последовательно (за 2 такта) заносятся в регистр множимого, а на управляющий вход формирователя дополнительного кода F2 поступает «1». Необходимо обеспечить выполнение алгоритма сложения чисел, представленных в форме с плавающей запятой, базируясь на схеме умножителя, реализующего заданный алгоритм умножения. Первое слагаемое переписывается в регистр результата под действием управляющих сигналов, поступающих на входы «h» всех ОЧУС (рис. 5). Если на вход «h» поступает «0», то ОЧУС перемножает разряды Мн и Мт и добавляет к полученному результату перенос из предыдущего ОЧУС. 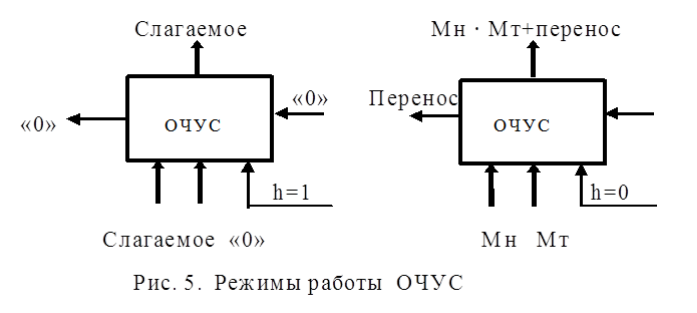 В ОЧС первое слагаемое складывается с нулем, записанным в регистре результата, и переписывается без изменений в регистр результата. На втором такте второе слагаемое из регистра множимого через цепочку ОЧУС попадает на входы ОЧС и складывается с первым слагаемым, хранящимся в регистре результата. Сумма хранится в регистре результата. Разрядность регистра результата должна быть на единицу больше, чем разрядность исходных слагаемых, чтобы предусмотреть возможность возникновения при суммировании переноса. Если устройство работает как умножитель, то множимое и множитель помещаются в соответствующие регистры, а на управляющий вход ФДК F2 поступает «0». Диада множителя поступает на входы преобразователя множителя. Единица переноса в следующую диаду, если она возникает, должна быть добавлена к следующей диаде множителя (выход 1 ПМ). В регистре множителя после каждого такта умножения содержимое сдвигается на 2 двоичных разряда, и в конце умножения регистр обнуляется. Это позволяет использовать регистр множителя для хранения младших разрядов произведения при умножении по алгоритму «Г». Выход 2 ПМ переходит в единичное состояние, если текущая диада содержит отрицание ( 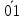 ). В этом случае инициализируется управляющий вход F1 формирователя дополнительного кода, и на выходах ФДК формируется дополнительный код множимого с обратным знаком (умножение на -1). Принцип работы ФДК в зависимости от управляющих сигналов отражен в табл.2. ). В этом случае инициализируется управляющий вход F1 формирователя дополнительного кода, и на выходах ФДК формируется дополнительный код множимого с обратным знаком (умножение на -1). Принцип работы ФДК в зависимости от управляющих сигналов отражен в табл.2. 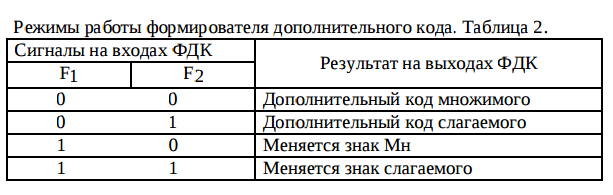 На выходах 3,4 ПМ формируются диады преобразованного множителя, которые поступают на входы ОЧУС вместе с диадами множимого (см. рис.2). На трех выходах ОЧУС формируется результат умножения диад Мн ∙ Мт + перенос из предыдущего ОЧУС. Максимальной цифрой в диаде преобразованного множителя является двойка, поэтому перенос, формируемый ОЧУС, может быть только двоичным: 3 ∙ 2 = 1 2. max maх max Мн Мт перенос Так как на входы ОЧУС из регистра Мт не могут поступить коды «3», в таблице истинности работы ОЧУС будут содержаться 16 безразличных входных наборов. Частичные произведения, получаемые на выходах ОЧУС, складываются с накапливаемой частичной суммой из регистра результата с помощью цепочки ОЧС (на первом такте выполняется сложение с нулем). Частичные суммы хранятся в регистре результата и регистре множителя, так как алгоритм умножения «Г» предполагает возможность синхронного сдвига этих регистров. Количество тактов умножения определяется разрядностью Мт. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

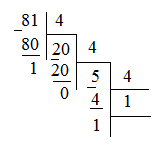
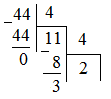
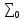
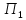 =Мн*
=Мн*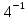
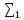
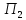 =
=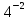
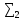
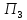 =
=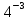
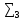
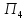 =0*Мн*
=0*Мн*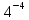
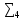
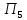 =
=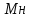 *
*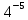
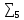
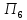 =
=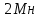 *
*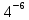
 =
=