методическая разработка урока. Разработка урока по дисциплине Высшая математика
 Скачать 60.46 Kb. Скачать 60.46 Kb.
|
|
ГБОУ Лукояновский Губернский колледж Методическая разработка урока по дисциплине «Высшая математика» «Основы алгоритмизации и программирования» Тема урока: «Приближенное вычисление определённого интеграла» Полосин М.М. Лукоянов 2017 Тема урока: «Приближенное вычисление определённого интеграла» Цель урока: Использование компьютерных технологий в высшей математике. Задачи урока: 1. Рассмотреть вычисление определенного интеграла в математике. 2. Автоматизировать вычисление не берущихся интегралов на компьютере. Ход урока 1.Орг.момент - 5 мин. 2.Объяснение нового материала – 15 мин. 3.Автоматизируем вычисление функции Лапласа на компьютере 15 мин 4. Подведение итогов урока – 5 мин 5. Домашнее задание – 5 мин 1. Орг. момент 2. Объяснение нового материала Рассмотрим еще одно применение степенных рядов к приближенным вычислениям. Это приближенное вычисление интегралов. До сегодняшнего дня мы вычисляли интегралы, которые с помощью таблицы интегралов и свойств интегралов относительно легко выражались в виде какой-то элементарной функцией. Но это далеко не так. Строго доказано, что они не интегрируемы в элементарных функциях. Так, например, интегралы 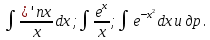 Нельзя представить никакими элементарными функциями. Однако эти интегралы существуют, но наших средств – всех основных элементарных функций – оказывается недостаточно, чтобы выразить их в конечном виде. Разъясним эту мысль. Допустим, что мы не имеем логарифмическую функцию. Тогда простейший интеграл 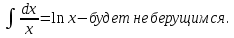 Но включив в рассмотрение логарифмическую функцию, мы легко выражаем этот интеграл в конечном виде. Поэтому не берущиеся интегралы так названы условно. Для того, чтобы сделать их берущимися можно рассчитать класс основных элементарных функций, которыми мы условились пользоваться. Но рассчитать до бесконечности уже устоявшийся класс элементарных функций приведёт к трудностям в изучении элементарной математики. Поэтому в математике и её приложениях пользуются приближенными методами вычисления не берущихся интегралов. Таких методов в математики существует несколько: Мы рассмотрим один них: вычисление не берущихся интегралов с помощью разложения интегральной функции в смешанный ряд. При изучении теории вероятностей важную роль играет функция 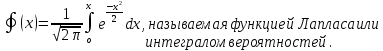 П.Лаплас(1749-1827) – выдающийся французский математик и физик, современник Лобачевского Н.И(1792-1856) Вычислить этот интеграл в конечном виде нельзя, т.к. он не выражается в элементарных функциях, т.е. относится к не берущимся интегралам. Разложим под интегральную функцию в ряд, используя разложение функции: 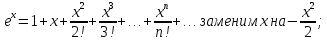 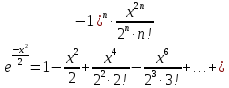 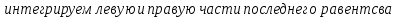 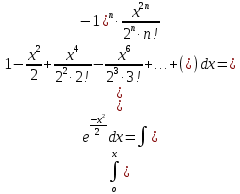 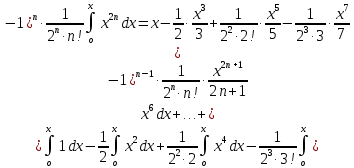 Для практического вычисления значения функции Лапласа, как правило, бывает достаточно трех – четырех членов ряда и значение функции находить с точностью четырех знаков после запятой: 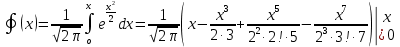 Для примера вычислим значение функции Лапласа при 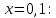 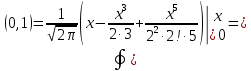 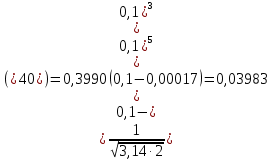 Табличное значение: 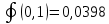 Эта таблица, составлена в своё время Лапласом, конечна. Переменная X в интеграле вероятности может принимать максимальное значение 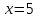 . Это связность тем, что функция . Это связность тем, что функция 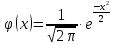 , если мы её исследуем на экстремум имеет максимальный при , если мы её исследуем на экстремум имеет максимальный при 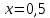 и это значение равно и это значение равно 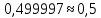 , что с точки зрения теории вероятности вполне понятно из школьного курса теории вероятности из очень известной задачи, связанной с бросанием монеты. , что с точки зрения теории вероятности вполне понятно из школьного курса теории вероятности из очень известной задачи, связанной с бросанием монеты.Таблица Лапласа, составленная шагом 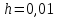 имеет 256 вычислительных значений. Я не случайно назвал годы жизни и творчества выдающегося ученого. В этот период основным средством вычислительной техники было таблица умножения, карандаш и бумага. Можно представить какой был труд при составлении этой таблицы. имеет 256 вычислительных значений. Я не случайно назвал годы жизни и творчества выдающегося ученого. В этот период основным средством вычислительной техники было таблица умножения, карандаш и бумага. Можно представить какой был труд при составлении этой таблицы.Сегодня, располагая выше изложенными математическими сведениями, современной вычислительной техникой, предлагаю вам составить программу для вычисления интеграла Лапласа и выдать нашу таблицу значений интеграла вероятностей только ещё раз запишу член разложения функций Лапласа в степенной ряд 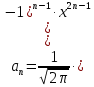 Не берущиеся интегралы: 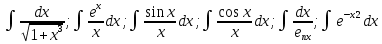 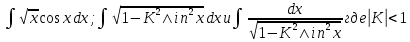 Кроме не берущихся интегралов встречаются интегралы, которые относятся к трудно берущимся. Конечно, это разделение очень условно. При вычислении интеграла необходима изобретательность и навык, которые приобретая практикой при решении достаточно большого числа примеров. Ведь не секрет, что для кого-то, например интеграл 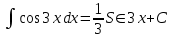 Будет трудно берущимся, хотя он вычисляется практически устно, если иметь соответствующие навыки. Пример: Вычислить интеграл: 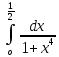 Решение: Этот интеграл условно можно отнести к трудно берущимся интегралам. Однако этот интеграл выражается в элементарных функциях 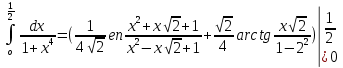 Если бы этот интеграл вычислили, то подсчитать его численное значение от О и от Если бы этот интеграл вычислили, то подсчитать его численное значение от О и от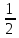 очень сложно, кроме того в результате подсчета мы не получим точного числа, т.к уже очень сложно, кроме того в результате подсчета мы не получим точного числа, т.к уже 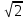 – иррациональное число и значения функций, входящих в состав первообразных интегралов, мы вычислим точное только приближенно. – иррациональное число и значения функций, входящих в состав первообразных интегралов, мы вычислим точное только приближенно.Разложим под интегральную функцию в ряд, используя разложение частного случая биноминального ряда: 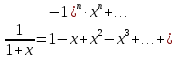 заменив заменив  на на 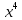 : :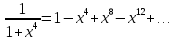 мы сразу получим мы сразу получим 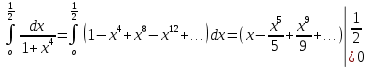 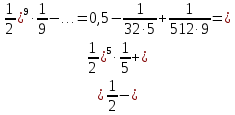 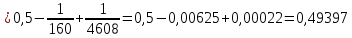 Если мы всё таки вычислим численное значение, полученной в результате интегрирования функции от 0 и от 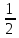 , учитывая, что , учитывая, что 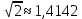 , то получим численное значение интеграла , то получим численное значение интеграла 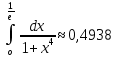 3. Автоматизируем вычисление функции Лапласа на компьютере (Огнёва Наталия Николаевна) 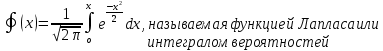 Член разложения функции Лапласа в степенной ряд 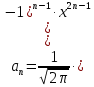 Разбор блок-схемы программы   Program My_1; Var x1, x2, P, e: real; i:real; a: real; Begin WriteLn ('Введите а'); ReadLn(a); i:=0; while (i begin P:=3.14; e:=a-(exp(ln(a)*3)/6)+(exp(ln(a)*5))/(8*6*7); x1:=1/(sqrt(2*P)); x2:=e*x1; i:=i+0.01; end; WriteLn(x2); End. Проверка работы программы получение значение функции Лапласа из таблицы
4. Подведение итогов урока Во время урока мы с вами подтвердили наши цели, что не возможно заниматься алгоритмизацией без знания математики. 5. Домашнее задание Домашнее задание: 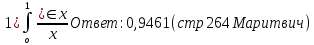  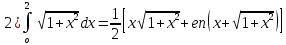 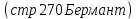 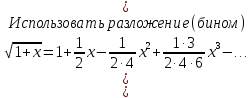 Дополнительные задачи Вычислить с точностью до 0,001 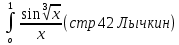 Решение: Представим под интегральную функцию в виде степенного ряда используя разложение в ряд 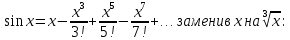 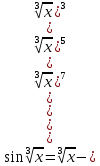 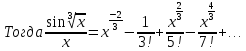 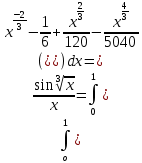 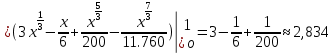 Вычислить с точностью до 0,001 интеграл 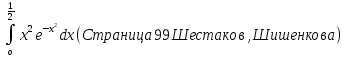 Решение: В разложении функции 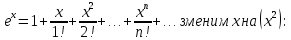 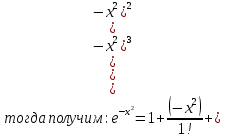 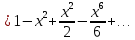 Умножим последний ряд численно на 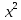 : :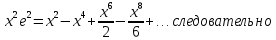 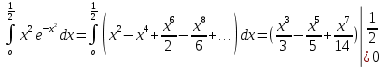 = = 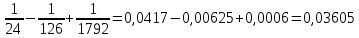 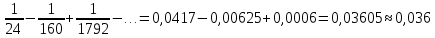 |
