Разработка усилителей мощности СВЧ диапазона. Разработка усилителей мощности свч диапазона
 Скачать 1.63 Mb. Скачать 1.63 Mb.
|
Глава 1. Исследование схемы с управляющим выходным аттенюаторомВ данной главе рассмотрен модуль усиления мощности СВЧ, построенный по схеме с возможностью регулировки коэффициента усиления посредством изменения коэффициента передачи аттенюатора на выходе усилителя, т. е. изменения затухания усиленного сигнала (Рис № 3). Схема модуль усиления с перестраиваемым выходным аттенюатором 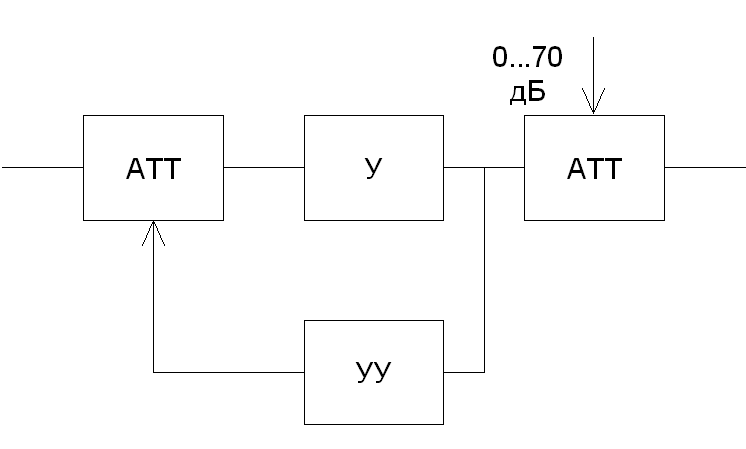 Рис. № 3 Такая схема построения модуля усиления СВЧ получила наиболее широкое распространение ввиду ряда важных достоинств: 1. так как управление коэффициентом усиления происходит на выходе усилителя, входной аттенюатор, сам усилитель и устройство управления находятся в одной рабочей точке, что позволяет не использовать широкодиапазонные приборы. 2. в ходе работы схемы не сказываются нелинейные свойства усилителя и блока управления входным сигналом, так как схема используется только в одной рабочей точке. . часть мощности на выходе усилителя подается на устройство управления, которое управляет коэффициентом передачи входного аттенюатора. Он, в свою очередь изменяет уровень входного сигнала. Таким образом, на выходе усилителя происходит высокостабильное поддержание необходимого уровня мощности. Наряду с вышеперечисленными достоинствами данная схема имеет очевидный недостаток. Так как управление коэффициентом усиления происходит в выходном аттенюаторе, есть вероятность получения недостаточной мощности на выходе прибора. Если увеличить мощность на выходе усилителя, есть большая вероятность выйти за пределы допустимой мощности работы выходного аттенюатора. На данном этапе исследований эта проблема так и не устранена, однако ввиду остальных достоинств такая схема употребляется в различных приборах наиболее часто. 1.1 Исследование устойчивости схемыПод устойчивостью системы понимают отсутствие в ней нарастающих во времени расходящихся свободных напряжений и токов, т е отсутствие самовозбуждения. В понятие «устойчивость усилителя» обычно вкладывается смысл стабильности его характеристик при различных дестабилизирующих факторах. Обеспечение устойчивости в диапазоне СВЧ представляет проблему значительно более серьезную, чем на низких частотах. Это обусловлено тем, что значения паразитных параметров при переходе к СВЧ диапазону не могут быть уменьшены пропорционально длине волны из-за физических и технологических ограничений и их влияние в этом диапазоне относительно увеличивается. Это относится и к пассивным цепям, нагружающим полупроводниковый прибор, поскольку нагрузки являются обычно частотно зависимыми и не всегда строго детерминированными. На СВЧ, наконец, значительно увеличивается абсолютный диапазон частот, в котором должна обеспечиваться устойчивость. В отличие от традиционных усилителей (например, резонансных усилителей высокой частоты), в которых самовозбуждение обычно происходит в рабочем диапазоне частот, в усилителях СВЧ оно чаще всего возникает вне рабочего диапазона. Поскольку устойчивость СВЧ полупроводниковых приборов в значительной степени определяется паразитными элементами, пренебрежение ими в моделях некорректно, а исследование устойчивости представляет собой сложную вычислительную задачу. Основной метод теории устойчивости заключается в исследовании с помощью определенных критериев моделей, представляющих с большей или меньшей достоверностью реальные устройства. Однако, поскольку нашей задачей является исследование устойчивости реального устройства, а не его модели, обязателен анализ корректности модели, т е определение степени ее соответствия реальному устройству. Прослеживается прямая связь отдельных этапов исследования устойчивости: требования теории, выраженные в форме критериев устойчивости, определяют вид модели (структурная, бесструктурная, физическая, экспериментальная) и требовании к точности ее параметров и, следовательно, к экспериментальной методике. При формулировании требований теории приходится учитывать и экспериментальные возможности здесь имеется следующая (назовем е обратной) связь: экспериментальные исследования позволят представить реальное устройство в виде определенной модели в определенном диапазоне частот, с определенной точностью; устойчивость модели, описанной таким образом, может быть исследована с помощью того или иного критерия; таким образом, модель обуславливает выбор критерия устойчивости. Ниже перечислены основные критерии устойчивости, наиболее часто применяемые на практике. Непосредственное определение корней характеристических уравнений обычно производят только в случае простейших схем, приводящих к дифференциальным уравнениям не выше второго порядка. Применение компьютерных методов обработки позволяет анализировать устойчивость систем значительно более высоко порядка. Устойчивость сложных моделей обычно приходится описывать дифференциальными уравнениями выше второго порядка. Непосредственное вычисление корней характеристических уравнений, соответствующих таким дифференциальным уравнениям громоздко, и для их анализа используют различные критерии устойчивости. К критериям, имеющим большую информативность, т. е. позволяющим выделить область устойчивости тех или иных параметров системы, относятся прежде всего алгебраические критерии. Большую информативность в указанном смысле имеет также метод D-разбиений, предложенный Неймарком. Данный критерий предлагает рассматривать устойчивость при изменении одного или нескольких параметров системы, что в свою очередь ведет к изменению ее характеристического уравнения. Приведем характеристическое уравнение замкнутой САУ к виду: где аттенюатор усилитель мощность микросхема частота Это уже другое уравнение и оно также имеет единственное решение (pн1 ,pн2 ,...,pнn ), отличающееся от (p1 ,p2 ,...,pn ). Если плавно менять значение параметра САУ, то коэффициенты уравнения тоже будут плавно изменяться, а его корни будут перемещаться по комплексной плоскости (рис.4). Перемещение корней характеристического уравнения по комплексной плоскости при изменении его коэффициентов 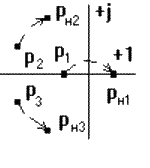 Рис. № 4 Каждый уникальный набору коэффициентов c1 ,c2 ,...,cn можно изобразить точкой в пространстве коэффициентов, по осям которого откладываются значения коэффициентов c1 ,c2 ,...,cn . Так уравнению третьей степени соответствует трехмерное пространство коэффициентов. Пусть точка N с координатами (cN1, cN2, cN3) соответствует уравнению, имеющему решение (pN1,pN2,pN3), точка M с координатами (cM1 ,cM2 ,cM3) соответствует уравнению, имеющему решение (pM1, pM2, pM3). При изменении какого-либо параметра САУ коэффициенты характеристического уравнения будут изменяться, при этом точка в пространстве коэффициентов, соответствующая данному уравнению будет перемещаться по некоторой траектории, например из положения N в положение M. Этому перемещению будет соответствовать и перемещение корней (pN1, pN2, pN3) на комплексной плоскости в положение (pM1, pM2, pM3) (аналогично рис.4). При этом движении некоторые корни будут переходить через мнимую ось комплексной плоскости из левой полуплоскости в правую и наоборот. В момент перехода такой k-й корень примет значение pK = jK, а коэффициенты уравнения будут иметь определенные значения cK1,cK2,cK3, определяющие в пространстве коэффициентов точку K. Подставим корень pK в характеристическое уравнение, получим тождество: Меняя w от - ∞ до + ∞, и находя при каждой частоте все возможные сочетания коэффициентов c1 ,c2 ,...,cn , удовлетворяющих уравнению можно построить в n-мерном пространстве коэффициентов сложную поверхность S, разделяющую его на области, называемое D-областями. Полученное уравнение называется уравнением границы D-разбиения. Переход из одной D-области в другую через поверхность S соответствует переходу одного или нескольких корней через мнимую ось в плоскости корней. То есть каждая точка внутри определенной D-области соответствует уравнению с определенным количеством левых и правых корней. Поэтому области обозначают D(m) по числу m правых корней. Достаточно взять любую точку в пространстве коэффициентов и найти для нее число правых корней. Затем, двигаясь по пространству коэффициентов через границу S, можно выявить обозначения всех других областей. Особый интерес представляет область D(0), которой соответствуют уравнения с полным отсутствием правых корней, называемая областью устойчивости. Описанный метод определения областей устойчивости называется методом D-разбиений. Не обязательно строить сложную n-мерную картину D-разбиения, можно изменять значения, например, только двух коэффициентов, оставляя другие коэффициенты постоянными. Границу D-разбиения S можно строить не только также и в пространстве конкретных параметров системы, от которых зависят данные коэффициенты. Известные критерии устойчивости - критерий Михайлова или критерий Найквиста, как его частный случай позволяют избежать определения корней уравнения и тем самым упростить рассмотрение устойчивости. Эти критерии позволяют судить об условиях устойчивости без определения положения корней на плоскости комплексной частоты. Ограничиваясь изучением поведения характеристического многочлена п-й степени на частотах, находящихся на оси jω плоскостир, можно выявить закономерности изменения аргумента (годографа) функции L(jω) И по этим закономерностям судить о существовании корней в правой полуплоскости комплексной частоты . Критерий устойчивости Найквиста позволяет судить об устойчивости замкнутой системы по виду АФЧХ разомкнутой системы. Пусть передаточные функции разомкнутой и замкнутой системы соответственно имеют вид: 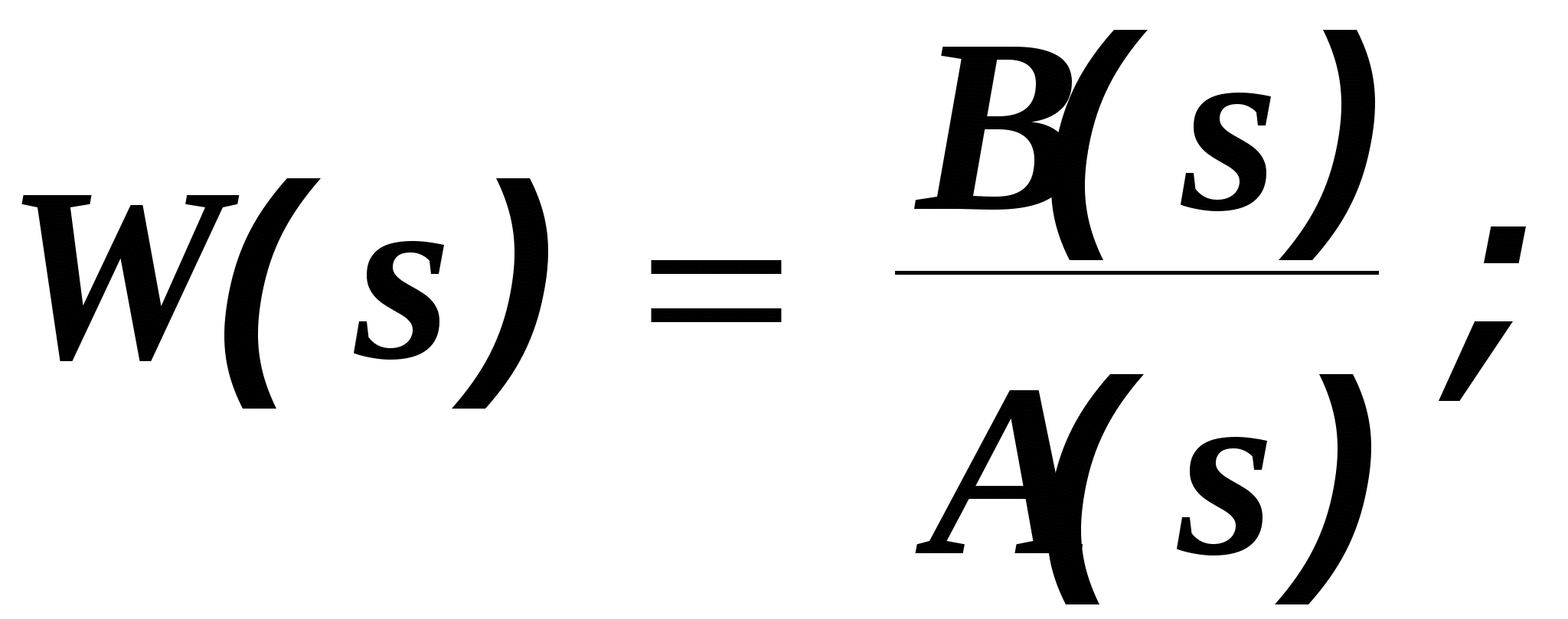 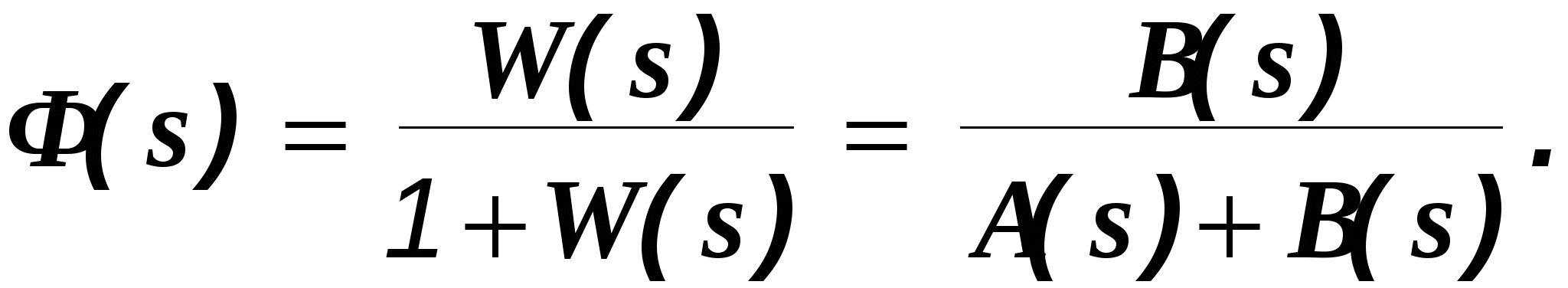 Введем функцию 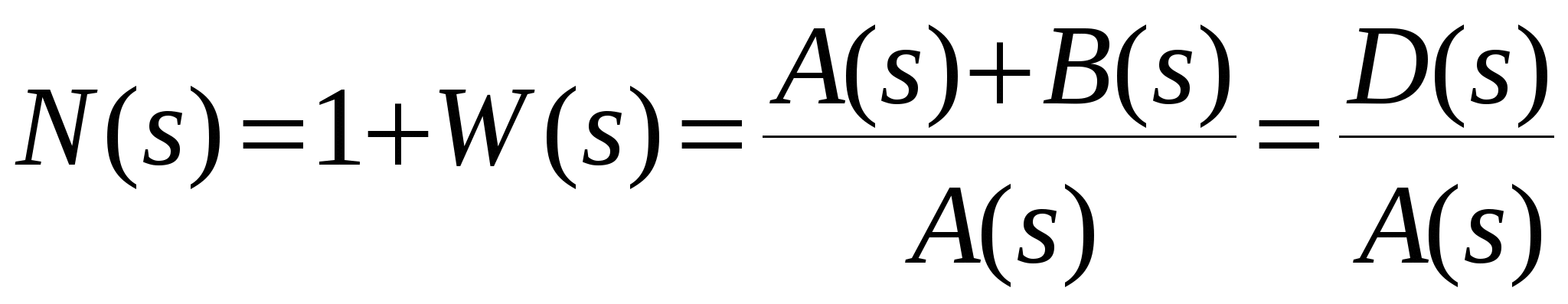 (1.6) (1.6)где D(s)- характеристический полином замкнутой системы. Перейдя к частотным представлениям, получим Вектор N(j) называется вектором Найквиста. Очевидно, что числитель и знаменатель этого вектора имеют один и тот же порядок n. При использовании критерия Найквиста следует различать два случая. ). Разомкнутая система устойчива и ее характеристическое уравнение A(s)=0имеет все корни в левой полуплоскости. Тогда при изменении частоты от 0 до 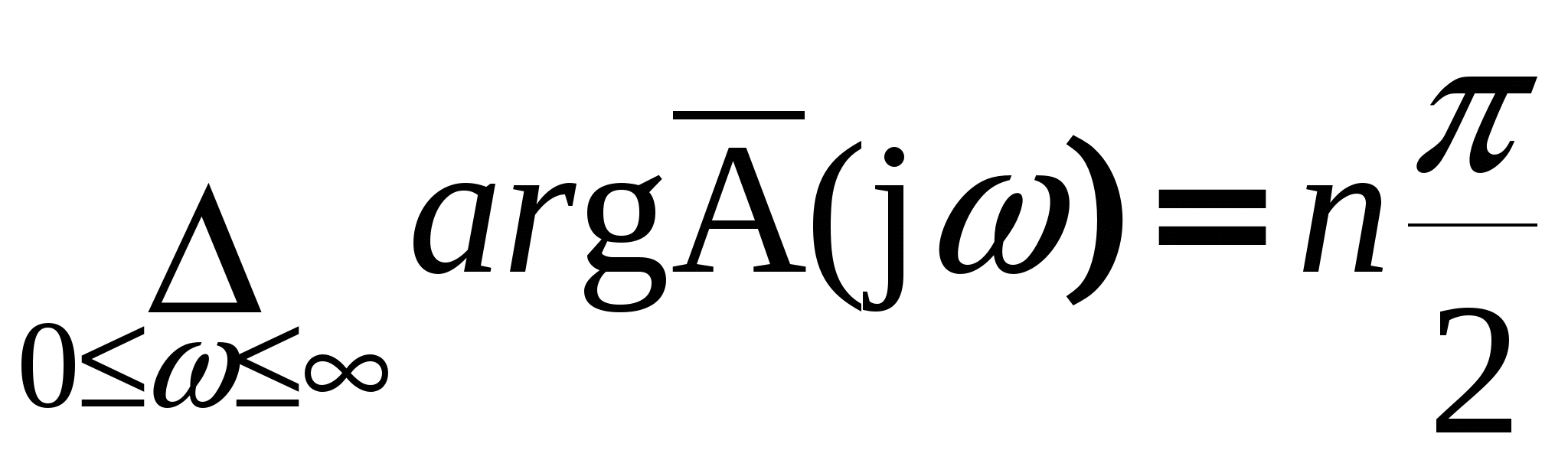 (1.8) (1.8)Изменение аргумента вектора D(j)в общем случае равно 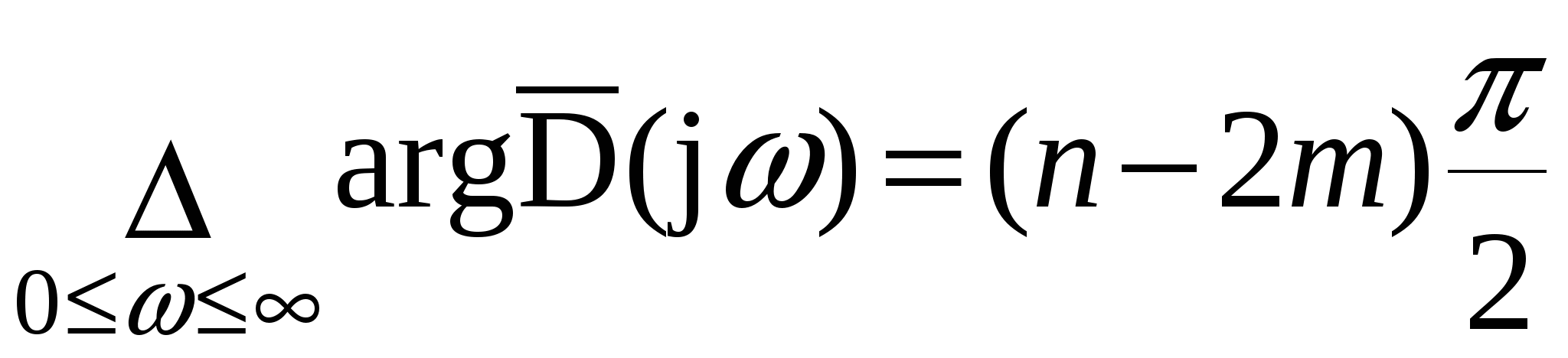 (1.9) (1.9)гдеm- число корней уравненияD(s)=0, лежащих в правой полуплоскости. Изменение аргумента вектора Найквиста будет 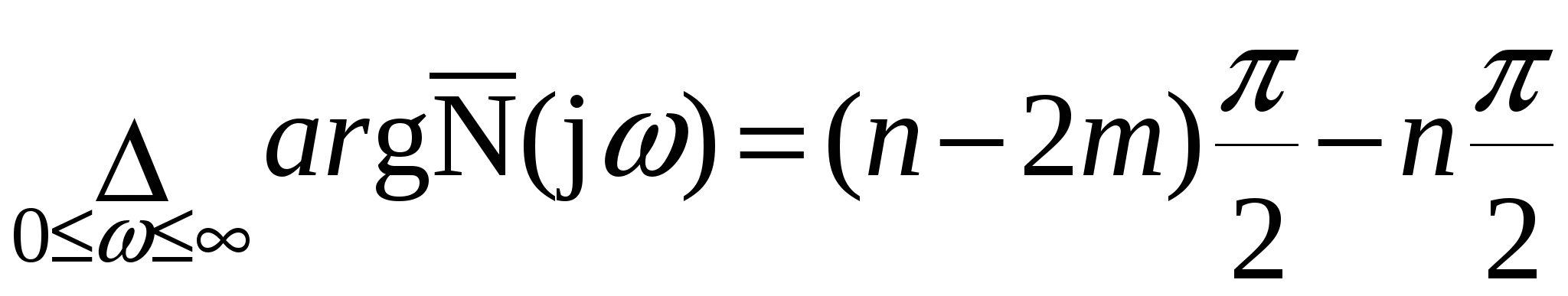 (1.10) (1.10)Если замкнутая система устойчива, то m=0 и 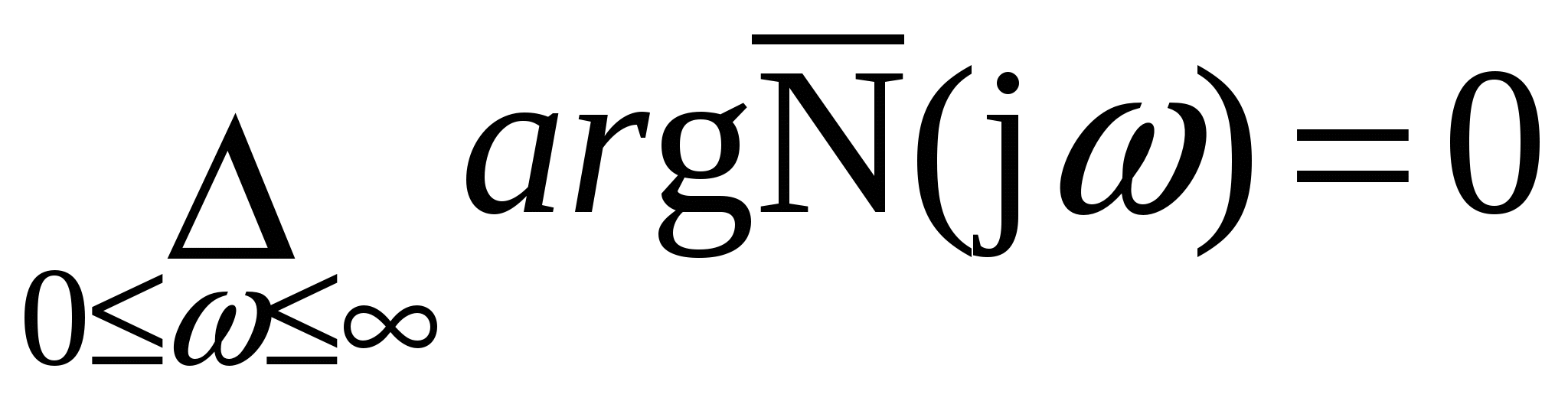 Так как при , W(j)0, то N(j)1. Рассмотрим рисунок 4(а), на котором показана кривая Найквиста, которую описывает вектор Найквиста при изменении частоты от 0 до . Нетрудно убедиться, что вектор Найквиста опишет угол, равный нулю только в случае, если его годограф не охватывает начало координат. Перенесем начало координат в точку с координатами (1,j0) (рис.4 б). Можно убедиться, что изменение аргумента вектора Найквиста будет равно нулю если АФЧХ W(j)разомкнутой системы не охватывает критическую точку с координатами (-1,j0). К определению критерия Найквиста 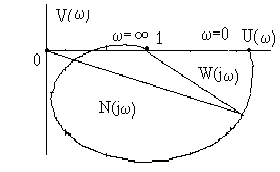 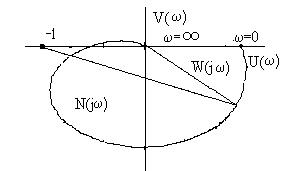 а) б) Рис. № 4. Критерий Найквиста для рассматриваемого случая формулируется следующим образом. Система, устойчивая в разомкнутом состоянии, будет устойчивой и в замкнутом состоянии, если АФЧХ W(j) разомкнутой системы при изменении частоты от 0 до не охватывает критическую точку с координатами (-1, j0). Особенности возникают, если разомкнутая система нейтрально-устойчива, т.е. 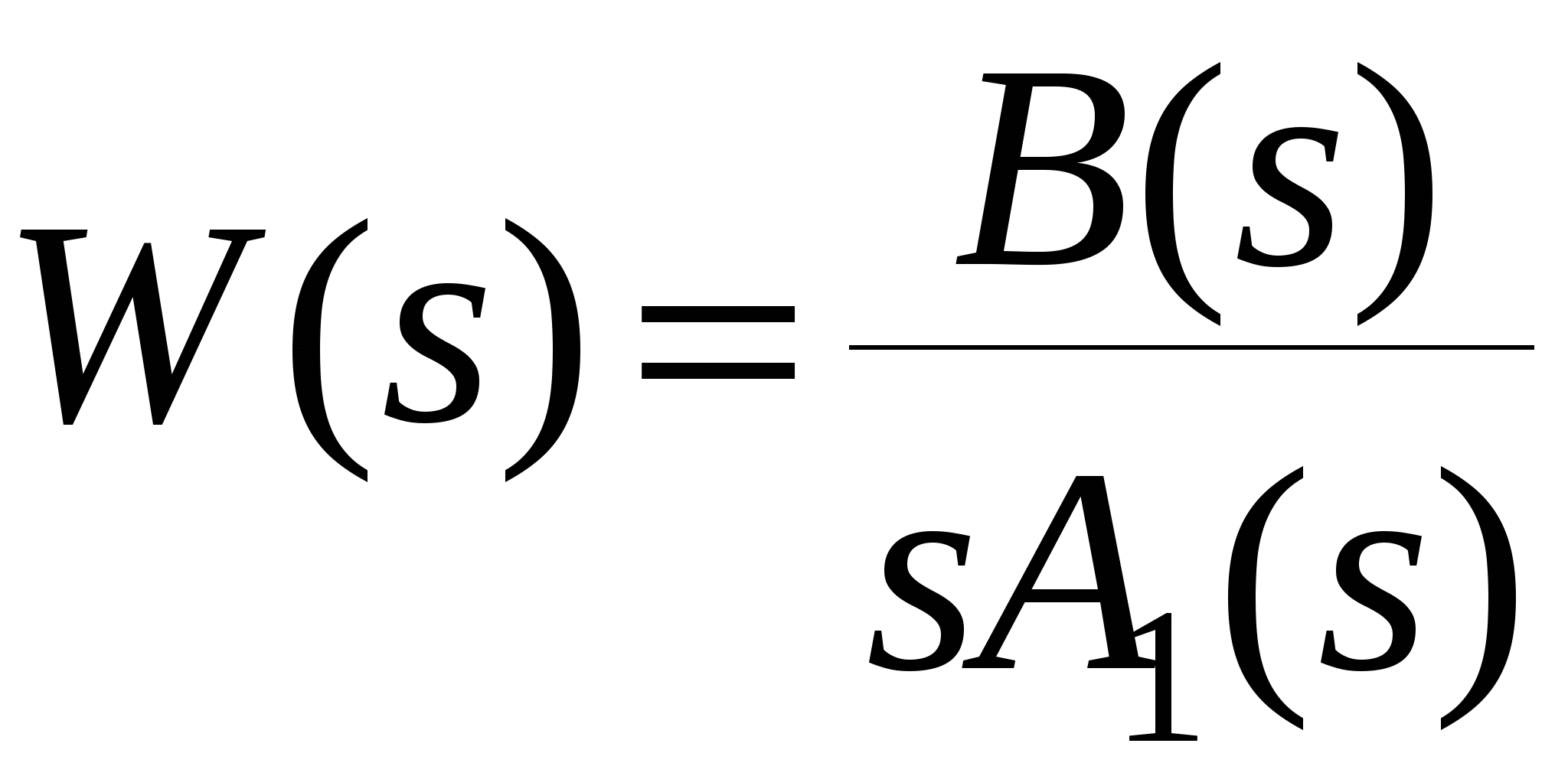 (1.11) (1.11)где полином A1(s) имеет все корни в левой полуплоскости. При =0АФЧХ разомкнутой системы W(j)= и проследить поведение кривой АФЧХ в окрестности этой точки невозможно. При изменении частоты от - до + наблюдается движение корней вдоль мнимой оси снизу вверх и при =0 происходит бесконечный разрыв. При этом движении обойдем нулевой корень (рис. 5) по полуокружности бесконечно малого радиуса так, чтобы этот корень остался слева, т.е. искусственно отнесем его к левой полуплоскости. Годограф Найквиста для нейтрально- устойчивой САУ 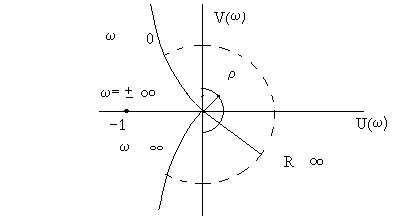 Рис. 5. При движении по этой полуокружности в положительном направлении независимая переменная изменяется по закону где фаза () изменяется от - / 2 до + / 2. Подставив это выражение в передаточную функцию вместо множителя s в знаменателе, получим 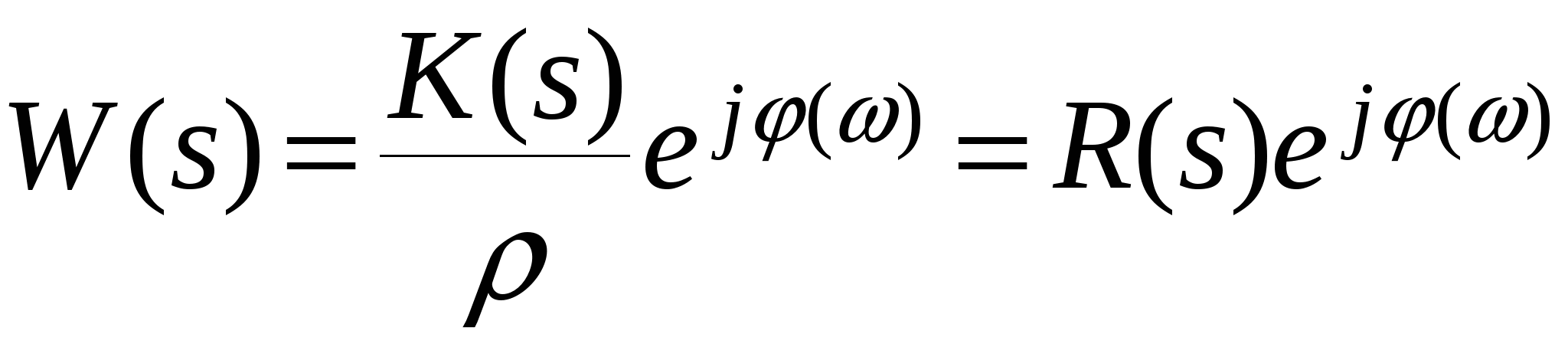 (1.12) (1.12)где Rпри 0 , а фаза () изменяется от + / 2 до - / 2. Следовательно, в окрестности нулевого корня годограф W(j) представляет собой часть окружности бесконечно большого радиуса, движение по которой происходит при увеличении частоты в отрицательном направлении. Для оценки устойчивости замкнутой системы, если разомкнутая система нейтрально устойчива, необходимо АФЧХ W(j) разомкнутой системы дополнить дугой бесконечно большого радиуса, начиная с меньших частот, в отрицательном направлении и для полученной замкнутой кривой воспользоваться критерием Найквиста для систем, устойчивых в разомкнутом состоянии. Разомкнутая система неустойчива. В этом случае 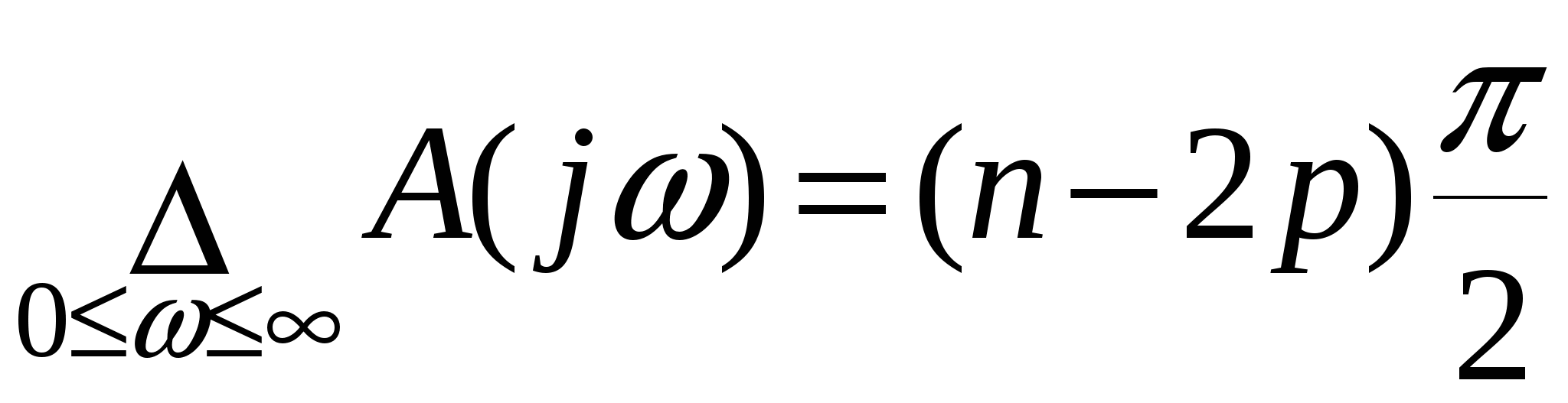 где р- число корней характеристического уравнения разомкнутой системы, лежащих в правой полуплоскости. Если замкнутая система устойчива, т.е. m=0, то 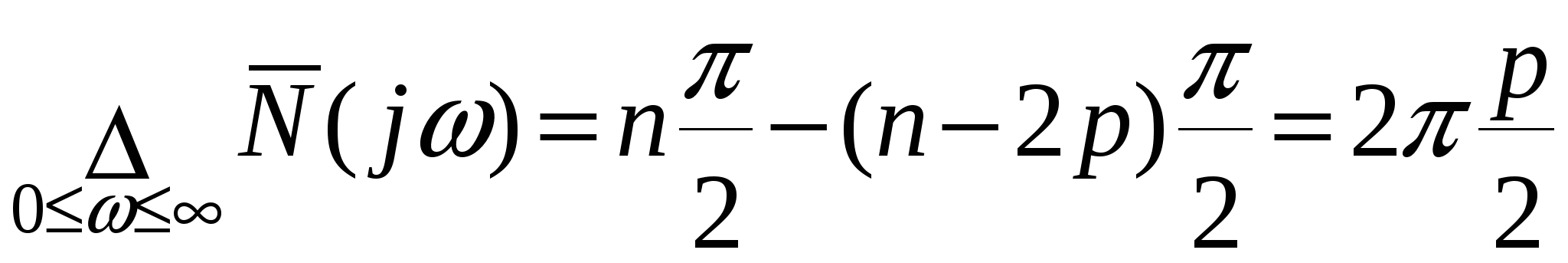 (1.13) (1.13)т.е. АФЧХ разомкнутой системы охватывает критическую точку (-1,j0) в положительном направлении ровно p / 2 раз. Система, неустойчивая в разомкнутом состоянии, будет устойчивой в замкнутом состоянии, если АФЧХ W(j с) разомкнутой системы при изменении частоты от 0 до охватывает критическую точку (-1,j0) в положительном направлении ровно р/2 раз, где р- число правых полюсов разомкнутой системы. Определение числа охватов критической точки- непростая задача, особенно в случае систем высокого порядка. Поэтому в практических приложениях нашла применение другая формулировка критерия Найквиста для рассматриваемого случая. Переход годографа W(j) через отрезок вещественной полуоси (-,-1), т.е. левее критической точки при увеличении частоты сверху вниз считается положительным, а снизу вверх- отрицательным. Система, неустойчивая в разомкнутом состоянии, будет устойчивой в замкнутом состоянии, если разность между числом положительных и отрицательных переходов АФЧХ разомкнутой системы равна р/2. 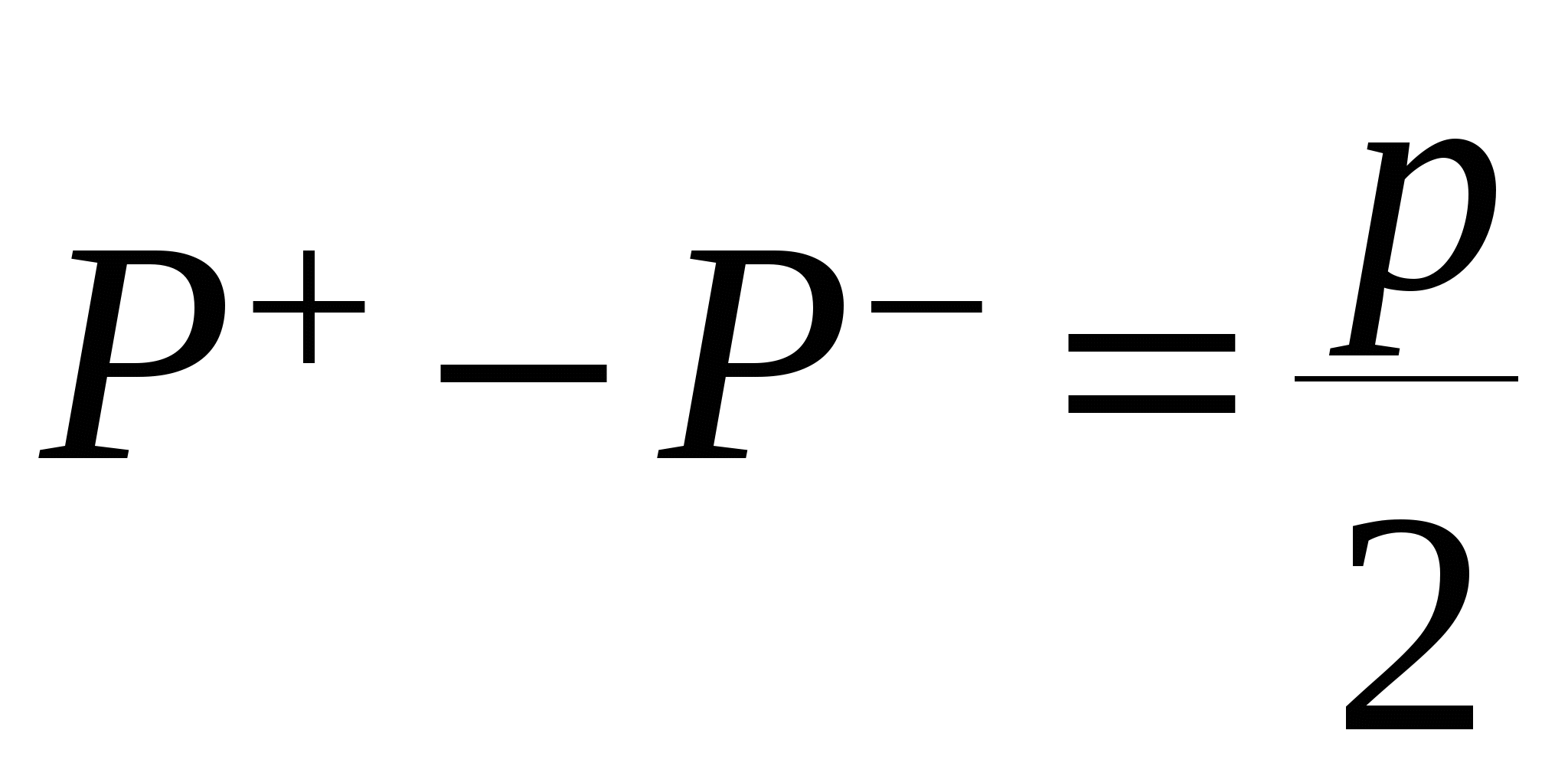 (1.14) (1.14)где
Устойчивость замкнутой САУ зависит от расположения годографа АФЧХ разомкнутой системы относительно критической точки. Чем ближе эта кривая проходит от критической точки, тем ближе замкнутая САУ к границе устойчивости. Для устойчивых систем удаление АФЧХ разомкнутой системы от критической точки принято оценивать запасами устойчивости по фазе и по модулю. Допустим, что АФЧХ некоторой разомкнутой системы имеет вид, показанный на рис 6 АФЧХ разомкнутой системы 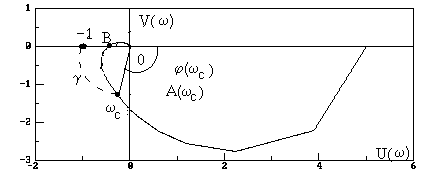 Рис. № 6. Угол , образуемый прямой, проходящей через точку пересечения АФЧХ с окружностью единичного радиуса, что соответствует частоте среза системы, и отрицательной вещественной полуосью называется запасом устойчивости системы по фазе. Запасом устойчивости по модулю называется величина 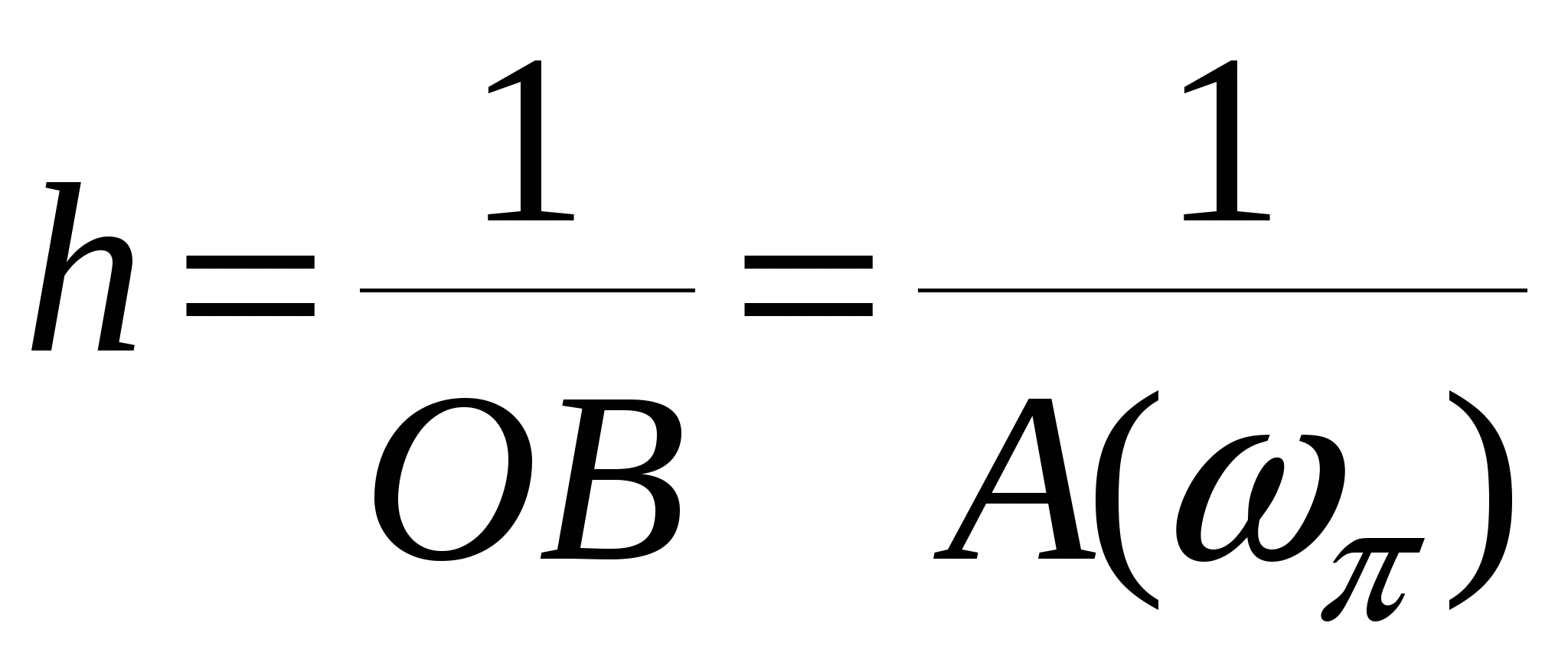 (1.16) (1.16)где А()- значение АФЧХ при частоте = , при которой она пересекает вещественную ось. Для всех систем должны выполняться требования: Так как АФЧХ графически строится в определенном масштабе, то для вычисления запаса устойчивости по модулю можно просто измерить длины отрезков, соответствующих единице и ОВ, и разделить результат первого измерения на второй. Если увеличивать коэффициент усиления системы, то точка В будет смещаться влево и при ОВ=-1 коэффициент усиления примет критическое значение. Поэтому запас устойчивости по модулю можно определить и по формуле 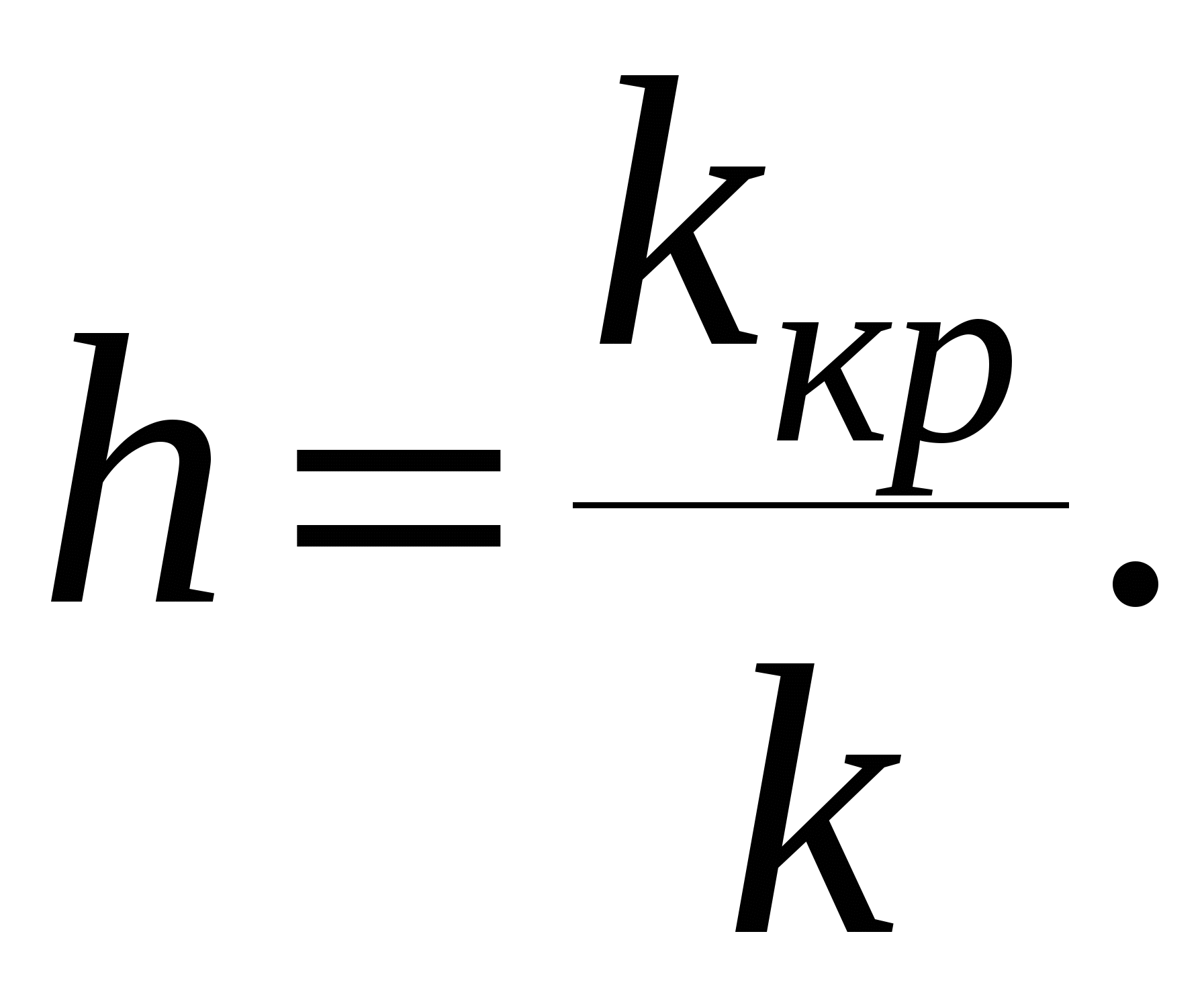 1.2 Исследование шумовых характеристик Шумы возникают в различных элементах устройств - в резисторах, конденсаторах, диодах и транзисторах. Относительно несложен анализ шумов на частотах выше приблизительно 5 кГц, где преобладают шумы дробового эффекта и тепловые шумы, пока на высоких частотах не начинает сказываться уменьшение коэффициента усиления активных элементов. На частотах ниже 5 кГц уровень экспериментально наблюдаемых шумов превосходит уровень тепловых шумов и шумов дробового эффекта и изменяется обратно пропорционально частоте - отсюда их название «Шумы типа 1/f». Шумы дробового эффекта. В активных элементах устройств протекание тока является процессом переноса отдельных электронов, движущихся как заряженные частицы. Флуктуации тока через элемент связаны с изменениями во времени числа электронов, проходящих через поперечное сечение полупроводникового прибора. Шоттки в 1918 г. показал, что среднеквадратичное значение флуктуаций тока где e=1.6·10-19 Кл - заряд электрона; I - постоянная составляющая тока через полупроводниковым прибор в амперах; Шумы дробового эффекта характеризуются гауссовским распределением амплитуды, поскольку вызваны очень большим числом независимых составляющих. Тепловые шумы. На проводниках возникает переменное напряжение, вызванное беспорядочным тепловым движением свободных электронов в объеме проводника. Согласно Джонсону и Найквисту среднеквадратическое значение напряжения холостого хода на любом проводнике может быть выражено как где k=1/3805·10-23 Дж/К - постоянная Больцмана; Т - абсолютная температура источника шума в кельвинах; R - сопротивление проводника в Омах; Тепловые шума также описываются гауссовским распределением амплитуды. В отличие от спектра шумов дробового эффекта, спектр этих шумов не зависит от частоты. Можно показать, что максимальная мощность источника тепловых шумов составляет kT Низкочастотные (1/f) шумы. Третий часто встречающийся вид с гауссовским распределением амплитуды - низкочастотные шумы, известные также под названием избыточных шумов или шумов фликкер-эффекта. Шумы этого вида связаны с контактными и поверхностными неоднородностями в полупроводниках и вызваны флуктуациями проводимости среды, через которую протекает ток. Спектральная плотность низкочастотных шумов (в ваттах), может быть описана выражением P(f)=k/fν где показатель степени ν изменяется в пределах от 0,8 до 1,5. Впервые шумы этого вида были обнаружены Шоттки в электровакуумных приборах и названы им «фликкер-эффектом», поскольку казались связанными с мерцанием электронной эмиссии катода. Такого же рода шумы наблюдаются в резисторах и конденсаторах. В отличии от шумов дробового эффекта и тепловых, низкочастотные шумы не считаются неустранимыми и могут быть снижены соответствующей технологией обработки поверхности полупроводниковых приборов. Высокочастотный усилитель можно рассматривать как умножитель частоты с коэффициентом умножения, равным единице. Таким образом, данное рассмотрение в равной мере применимо как к усилителям, так и к умножителям частоты. Экспериментально показано, что спектральная плотность фазовых шумов, возникающих в усилителях и умножителях частоты (остаточных шумов), изменяется по закону 1/f на частотах от 1 Гц до 5 кГц и что шумы этого типа являются результатом непосредственной фазовой модуляции высокочастотного колебания, проходящего через устройство, в активных элементах последнего. В отсутствии отрицательной обратной связи по высокой частоте типичное значение α(1) (величина фазовых шумов при отстройке 1 Гц) лежит в пределах от -110 до -120 дБ и определяется типом используемого транзистора. Типичное значение СПМ фазовых шумов, пересчитанное ко входу устройства составляет приблизительно α(fm)=-112+10lgfmдБ. (Это справедливо для кремниевых и германиевых полевых и биполярных транзисторов с любыми граничными частотами, с любым уровнем шумов фликкер-эффекта, независимо от типа корпуса.) Снижение шумов достигается только введением отрицательной обратной связи по высокой частоте. Таким образом можно получить снижение уровня фазовых шумов на 30-40дБ. Экспериментально показано, что на величину α(1) не оказывают существенного влияния ни значения рабочей частоты (в пределах до сотен мегагерц), ни уровень мощности входного колебания (при изменении последнего в разумных пределах). Не наблюдается также зависимости α(1) ни от режима работы усилителя (в классах А, В и С), ни от коэффициента умножения (включая единичный). При частотах анализа свыше 5кГц преобладающими оказываются тепловые шумы. Величина отношения мощности одной боковой полосы частот шумов к мощности несущей определяется уровнем входной мощности, уровнем собственных тепловых шумов и коэффициентом шума устройства. Это отношение в полосе частот шириной 1 Гц, отнесенное ко входу, равно α(fm=1Гц)=10lg(kT/Pвх)+F, где Pвх- высокочастотная мощность на входе устройства; kT =4·10-21;F -коэффициент шума устройства в децибелах. На практике входное колебание также может обладать значительным уровнем фазовых шумов. Если рассматриваемое устройство представляет собой умножитель частоты на n, то эти шумы на выходе умножителя будут усилены на 20lg(n) дБ. Повышение требований к характеристикам малошумящих СВЧ транзисторных усилителей для приемных трактов систем передачи вызывает необходимость полного и точного определения сигнальных и шумовых параметров транзистора. При этом надо стремиться как к уменьшению этапа эскизного проектирования, так и к сокращению этапа оптимизации усилителя на ЭВМ, что можно достичь рациональным выбором системы описания СВЧ транзистора. Известные соотношения | для расчета шумовых характеристик СВЧ транзисторов по физическим эквивалентным шумовым схемам и следующие из них выводы получены при использовании упрощенных эквивалентных схем и ряда допущений, приводящих при расчетах шумовых характеристик СВЧ транзисторных усилителей к большим погрешностям. Экспериментальное определение первичных шумовых параметров СВЧ транзисторов в системе S-параметров достаточно трудоемко и может быть проведено с относительно большой погрешностью, достигающей 40%, что ограничивает практическое использование этих параметров. Рассмотрим другой возможный способ описания первичных шумовых параметров СВЧ цепей, методику их измерения и расчета по полной эквивалентной схеме, найдем взаимосвязь параметров в различных схемах включения транзистора. Шумовые свойства транзистора будем характеризовать теоретическим коэффициентом шума F и мерой шума Мш Шумовые параметры транзистора. СВЧ транзистор как автономный четырехполюсник может быть описан волновыми параметрами, из которых наибольшее практическое применение получили S-параметры (рассеяния) и T-параметры (передачи). T-параметры реже используются на практике, хотя, как будет показано ниже, их использование для анализа свойств СВЧ транзисторов значительно упрощает расчет шумовых характеристик усилителей. Уравнение автономного четырехполюсника в системе нормированных T-параметров имеет вид 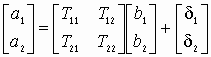 (1.20) (1.20)здесь При расчетах шумовых характеристик СВЧ цепей запись всех формул упрощается, если использовать элементы нормированной матрицы спектральных плотностей 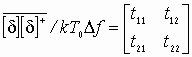 (1.21) (1.21) где индекс (+) означает эрмитово сопряженную матрицу. Элементы t i,j являются первичными шумовыми параметрами СВЧ автономного четырехполюсника в системе T-параметров. Расчет шумовых характеристик. Рассмотрим шумовые характеристики транзистора при подключении к нему источника сигналов с коэффициентом отражения Гг и произвольной нешумящей нагрузки. Исследуя пути прохождения шумовых волн в цепи, получим выражение для коэффициента шума 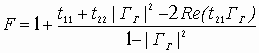 (1.22) (1.22)которое легко преобразуется к виду 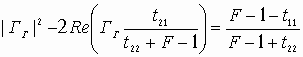 (1.23) (1.23)Соотношение (1.23) есть уравнение окружности постоянного значения коэффициента шума на плоскости Гг с центром 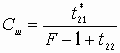 (1.24) (1.24)и радиусом 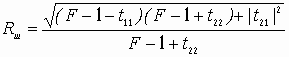 Приравнивая радиус Rш к нулю, получим минимальное значение коэффициента шума Fмини соответствующее ему значение оптимального коэффициента отражения источника сигнала Гг.ш.: Для расчета меры шума учтем, что где 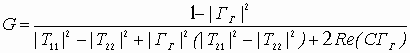 (1.25) (1.25)номинальный коэффициент передачи по мощности, здесь 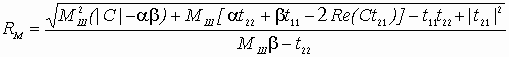 где 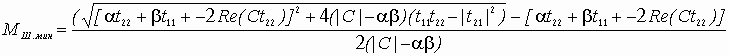 и оптимальное значение коэффициента отражения генератора сигналов 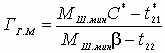 Определение шумовых параметров. Из вышеприведенных соотношений следует, что, определив экспериментально величины Fмин, Гг.ш и коэффициент шума транзистора в стандартном тракте Гo, т. е. при Гг=0, можно рассчитать искомые шумовые параметры 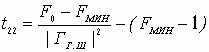 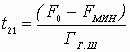 ; ; Так как коэффициенты шума могут быть измерены с малой погрешностью, точность измерения параметров ti,j полностью определяется погрешностью измерения величины ГГ.Ш, которая практически может быть снижена до 5-10%. Поэтому точность экспериментального определения первичных шумовых t-параметров значительно выше, чем при измерении шумовых параметров в 5-системе. При использовании транзистора на высоких частотах в схеме с общим эмиттером (ОЭ) можно считать В ряде случаев при расчете СВЧ транзисторных усилителей на ЭВМ предпочтительней использовать полную физическую эквивалентную схему транзистора, шумовые источники учитываются обычным способом. На первом этапе такого расчета проще определить параметры транзистора в Y-системе, т. е. вычислить Y-параметры и элементы матрицы шумовых токов короткого замыкания [Iш], после чего найти искомые параметры в Y-системе по соотношениям 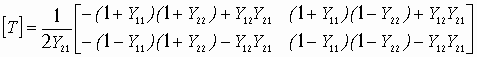 (1.26) (1.26)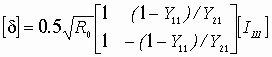 (1.27) (1.27)где Rо - сопротивление нормировки; Yi,j - нормированные по Rо Y-параметры транзистора. Отметим, что полученные выше формулы для коэффициента шума и меры шума проще соответствующих формул в системе S-параметров, а экспериментальное определение первичных шумовых t-параметров менее трудоемко и более точно. Но особенно заметно преимущество использования параметров в T-системе сказывается при анализе и параметрическом синтезе многотранзисторных СВЧ усилителей (каскадных и многокаскадных), так как для каскадного соединения N четырехполюсников общая T-матрица усилителя определяется в виде а автономные параметры Эти соотношения содержат лишь операции сложения и умножения, что приводит к сокращению требуемого машинного времени при упрощении алгоритма расчета. Аналогичные формулы в системе S-параметров более громоздки и неудобны при машинном анализе сложных соединений шумящих СВЧ цепей. Целесообразность использования шумовых t-параметров подтверждают результаты исследования шумовых свойств СВЧ балансных усилителей. Естественно, что практически можно использовать и смешанную систему параметров, т. е. неавтономные параметры описывать в S-системе, а автономные - шумовыми t-параметрами. В этом случае при экспериментальном определении всех параметров транзистора может быть достигнута наибольшая точность расчетов, так как эти параметры определяются экспериментально с наибольшей точностью. Взаимосвязь шумовых параметров транзистора в различных схемах включения. Так как наибольшее распространение в СВЧ диапазоне получила схема включения транзистора ОЭ, то выразим шумовые параметры транзистора в схемах с общей базой (ОБ) и с общим коллектором (ОК) через параметры схемы ОЭ. Для этого случая были получены соотношения: 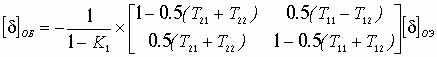 (1.27) (1.27)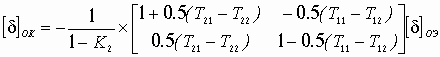 (1.28) (1.28)где параметры Тi,j определены для схемы ОЭ. При выводе этих соотношений не использовались какие-либо допущения, поэтому они справедливы для любого частотного диапазона. Отметим, что аналогичные соотношения в системе S-параметров настолько громоздки, что практически не используются. Из анализа (1.26) и (1.27) следует, что шумовые параметры транзистора в различных схемах включения отличны друг от друга. Поэтому при произвольной проводимости источника сигнала коэффициенты шума транзистора в схемах ОЭ, ОБ и ОК не равны. Однако можно найти условия, определяющие области равенства коэффициентов шума этих схем. Так, свойства схем ОЭ и ОБ примерно равны, если Соответственно коэффициенты шума схем ОЭ и ОК равны, если Зависимости первичных шумовых параметров от тока эмиттера 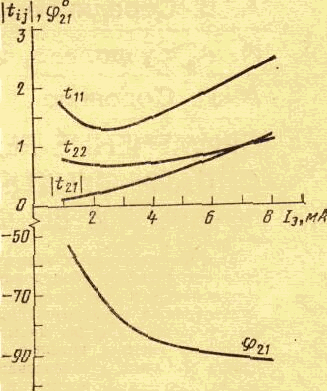 Рис. № 7 По предложенной методике были измерены шумовые t-параметры ряда отечественных СВЧ транзисторов. На рис. 7 приведены зависимости t-параметров от тока эмиттера 1Э на частоте 3,6 ГГц для транзистора КТ391 Зависимости минимального коэффициента шума от тока эмиттера в трех схемах включениях 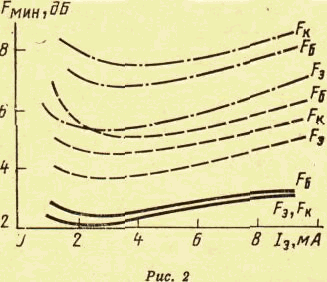 Рис. № 8 на рис. 8 - зависимости минимального значения коэффициентов шума транзистора КT391 для трех схем включения на частотах 1 ГГц (сплошные линии), 3,6 ГГц (пунктирные линии) и 5 ГГц (штрихпунктирные линии). Выводы: 1. Использование параметров СВЧ транзистора в T-системе значительно упрощает экспериментальное определение первичных шумовых параметров и анализ шумовых характеристик многокаскадных усилителей. 2. Полученные соотношения позволяют оценить шумовые свойства транзистора в различных схемах включения, что облегчает выбор схемы усилителя при заданных требованиях на шумовые характеристики. 3. Применение T-параметров транзисторов позволило при параметрическом синтезе многокаскадного усилителя на элементах с распределенными постоянными сократить на 40% машинное время по сравнению со случаем использования S-параметров. |
