81. Статистические методы, фильтрация и анализ спектров

• Название: 81. Статистические методы, фильтрация и анализ спектров
• Дата: 21.10.2022
• Размер: 0.98 Mb.
• Имя файла: 10685811_Otvetykbiletam8.docx
• Тип: Задача; #747398
• страница: 1 из 20

81. Статистические методы, фильтрация и анализ спектров

Спектральный анализ является одним из методов обработки сигналов. Его основная задача - выявление частотного спектра этих сигналов, или, другими словами, определение гармонических составляющих сигнала, их амплитуд и начальных фаз. Преобразование Фурье является математической основой метода, который связывает временной или пространственный сигнал и его модель с его представлением в частотной или волновой области. Фурье анализ предоставляет возможность разложения любого периодического сигнала в бесконечную, но счетную сумму отдельных гармонических составляющих. Все сигналы, как правило, имеют шумовую или случайную составляющую, тогда получаемые характеристики известны не точно или не могут быть определены без погрешности, поэтому по некоторому отрезку сигнала мы можем получить лишь оценку его спектра. Если сигнал в основном является случайным, то его спектральная оценка обычно характеризуется спектральной плотностью мощности или амплитуды. И одной этой оценки не достаточно. Поэтому поведение и характеристики случайных сигналов должны описываться с помощью статистических критериев. К задачам статистического анализа процессов относится определение спектральных плотностей мощности и корреляционных характеристик. Но, в отличие от спектральной оценки, спектральная плотность мощности не дает информации о гармониках сигнала.

Спектральный анализ заключается в разложении сигнала на его частотные или спектральные составляющие и оценке или измерении их характеристик – амплитуды, фазы, мощности, спектральной плотности мощности и др.

Основными методами спектрального анализа являются фильтровые (методы полосового анализа), бесфильтровые (основанные на ДПФ), параметрические (на основе параметрических моделей случайных процессов), текущего, скользящего и скачущего анализа.

К параметрам анализаторов спектра относятся: число каналов анализа; время наблюдения или анализа (ширина окна) и соответствующее ему число отсчетов или длина обрабатываемой реализации; полоса анализа, не превышающая для дискретных сигналов основной полосы спектра; разрешение по частоте, обратное, пропорциональное времени анализа и соответствующее разности частот двух соседних разрешаемых (разделяемых) частотных составляющих сигнала.

6.1. Спектральный анализ стационарных гармонических сигналов

Предполагается, что спектр аналогового сигнала x(t) сосредоточен в ограни­ченной полосе частот и, следовательно, его параметры могут быть оценены с помощью спектральных характеристик дискретного эквивалента x[n], который формируется после предварительной аналоговой фильтрации на выходе АЦП. Эффекты наложе­ния и шумы цифрового преобразования не учитываются. Параметры гармонического сигнала, такие как, амплитуда, фаза и частота не изменяются во времени.

Для таких сигналов спектральный анализ может быть выполнен с помощью дискретного во времени преобразования Фурье (ДВПФ):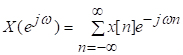

.

На практике для анализа используется последовательность  , которая определяется как произведение дискретного сигнала x[n] на весовую функцию w[n] на конечном интервале N. В качестве оценки спектра  берется спектр взвешенной последовательности  ,  , который вычисляется с помощью R-точечного ДПФ (БПФ), (R ³ N) (рис. 14).

Переход к дискретным частотам осуществляется в точках

.

Дискретные частоты  связаны с номером отсчета ДПФ соотношением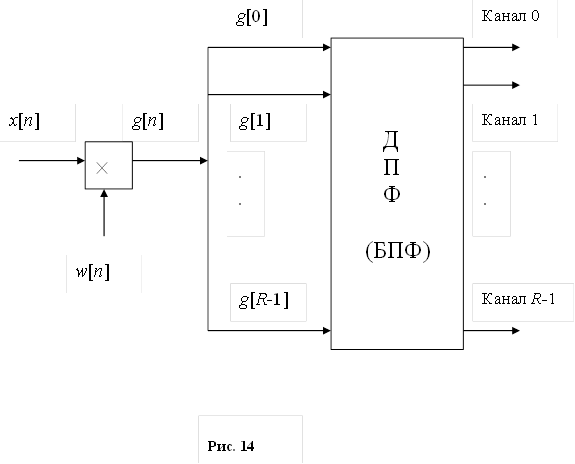

 



.                                                               (100)

При этом номер k коэффициента ДПФ связан с частотой сигнала fc и частотой дискретизации   соотношением

.                                                                 (101)

Выход канала ДПФ G(k) совпадает с выходом нерекурсивного фильтра с импульсной характеристикой, отвечающей условию

 или  .

Такой фильтр имеет частотную характеристику

,

являющуюся комплексно-сопряженной частотной характеристикой весовой функции  , смещенной вправо (или влево) к частоте wk.

Для анализатора с прямоугольной весовой функцией

.

Частотная характеристика имеет главный лепесток шириной   с относительным уровнем максимального бокового лепестка dбл= –13,6 дБ.

Однозначное разрешение комплексного гармонического сигнала имеет место только на частотах, совпадающих с частотами анализа ДПФ, когда в интервале анализа укладывается целое число периодов сигнала. В этом случае сигнал присутствует только на выходе одного канала (или иначе) проецируется на один бин ДПФ.

На сигналы с частотой, не равной wk , откликаются два соседних канала на уровне главных лепестков их частотных характеристик, а на уровне боковых лепестков откликаются все каналы ДПФ. Это явление называют размыванием спектра или эффектом просачивания.

Пример. Предположим, что анализируется сигнал  ,  . Представим его в виде

.

Дискретное во времени преобразование Фурье дает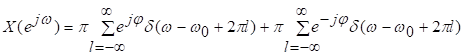

.

Пусть частота сигнала fc = 10 Гц, размер ДПФ R =32, частота дискретизации f¶ = =64 Гц. Тогда k = 10×32/64 = 5. Спектр ДПФ будет содержать два отличных от нуля коэффициента X(5) и X(32-5=27).

Если частота сигнала fc = 11 Гц, при таких же условиях получаем

.

Отсчет дискретного во времени преобразования Фурье для частоты fc = 11 Гц будет располагаться между коэффициентами спектра ДПФ с номерами k=5 и k=6. Происходит размытие спектра сигнала на выходе спектроанализатора. При введении прямоугольного окна 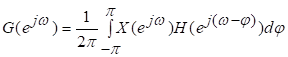  и

.

ДВПФ   определяется в виде частотного сдвига на   частотной характеристики весового окна  с учетом масштабирующего множителя 0,5. В частотном диапазоне   это проявляется в виде двух пиков на частотах 0,344p и 2p(1-11/64)=1,656p/

Влияние весовой функции. Высокий уровень боковых лепестков и обусловленное им сильное влияние каналов анализатора спектра является основным недостатком прямоугольной весовой функции. Эти недостатки преодолеваются с помощью специальных весовых функций, имеющих меньший уровень боковых лепестков. Наиболее известны весовые функции:

·        Хэмминга  , dбл= -43 дБ, D=8p/N;

·        Блакмана  , dбл= -58 дБ и др.

Однако при этом возрастает ширина главного лепестка, что приводит к ухудшению разрешающей способности. Улучшение разрешения анализатора спектра с весовыми функциями обеспечивается путем увеличения числа точек ДПФ, т. е. увеличением времени анализа сигнала.

6.2. Статистические методы спектрального анализа

Для стационарного в широком смысле случайного процесса x[n] среднее не зависит от времени, а корреляция зависит только от разности индексов.

Математическое ожидание от случайной величины x[n] (или среднее) есть

.

Автокорреляционная функция определяется как

.                                   (120)

На практике имеется последовательность ограниченной длины x[n], n=0,…,N-1, поэтому вычисление по (120) невозможно и в качестве оценки корреляционной функции принимается величина

.                               (121)

Это оценка называется несмещенной оценкой корреляционной функции, так как ее математическое ожидание будет равно истинной автокорреляционной оценке: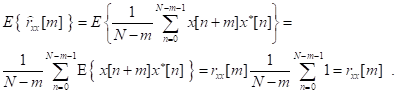



Кроме (121), на практике часто используют смещенную оценку корреляционной функции: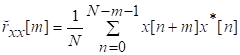

.                                    (122)

Эта оценка называется смещенной оценкой корреляционной функции, так как ее математическое ожидание будет равно ортонормированной истинной автокорреляционной оценки: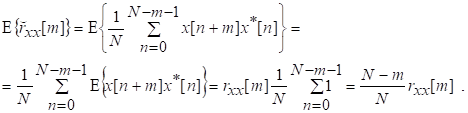



Учитывая (121) и (122), можно показать, что смещенная и несмещенная автокорреляционные функции связаны соотношением

.                                                      (123)

Как смещенная, так и несмещенная оценка удовлетворяет соотношению

                                                                (124)

и сохраняет полную мощность сигнала

.

Для взаимно корреляционной функции соотношения (120), (121) и (122) выглядят следующим образом: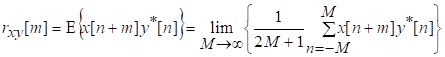

,               (125)

,                                  (12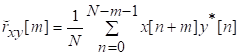6)

.                                     (127)

В общем случае для взаимной корреляции соотношение (124) не выполняется  , но выполняется соотношение вида 

Коррелограммный метод оценки. По теореме Винера-Хинчина корреляционная функция и спектральная плотность мощности (СПМ) связаны преобразование Фурье: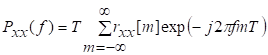

,                                     (128)

где T - интервал дискретизации сигнала. На практике для вычисления СПМ используют ограниченную сумму, в которой вместо истинной оценки корреляционной функции выбирают оценку из соотношений (121) или (122). Пусть мы получили несмещенную оценку корреляционной функции из соотношения (121) для максимально возможного корреляционного сдвига L, тогда для вычисления СПМ формулу (128) перепишем в виде

.                     (129)

На практике L берут много меньше длины последовательности. L<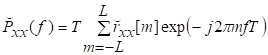
.                                   (130)

Корреляцию при положительных индексах можно получить, использую соотношения (121) и (122), отрицательные индексы должны удовлетворять соотношению (124).

Коррелограммный метод оценки СПМ можно дополнить, умножив корреляционную функцию на функцию окна:

,

где w[n] - функция весового окна. Выбор весового окна должен определяться из следующих соображений:

,                     (131)

где   - Фурье-преобразование функции окна. Из (131) следует, что желательно выбирать такие окна, у которых   во всей области частот.

Алгоритм коррелограммной оценки.

1.  Выбрать последовательность x[n], n = 0,…, N-1.

2.  Вычислить корреляционную функцию по соотношениям (121) или (122) для максимального корреляционного сдвига L (L << N).

3.  Выбрать число отсчетов в частотной области. Пусть M - число отсчетов в области частот от [-Fd/2; Fd/2], где Fd  - частота  дискретизации. Должно выполняться условие 2L < M. Определить функцию корреляции из условия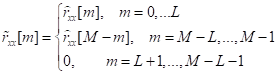

.

4              Умножить   на функцию окна.

5              Вычислить Фурье преобразование и разделить на мощность окна.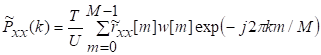

,

где  .

Взаимная спектральная плотность мощности определяется соотношением



Дальнейшие рассуждения аналогичны СПМ, за исключением использования вместо автокорреляции взаимной корреляции.

Периодограммная оценка СПМ. Определение СПМ основывается еще на эргодичности процесса, когда усреднение по ансамблю заменяется усреднением по времени.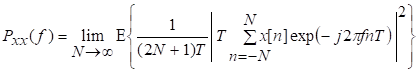

               (132)

Если не учитывать операцию математического ожидания, то можно придти к соотношению вида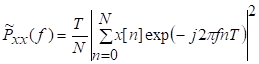

.

Данная оценка получается несостоятельной и на практике редко применяется. Для получения состоятельной СПМ необходимо заменить математическое ожидание усреднением по времени.

Алгоритм СПМ имеет следующий вид.

1. Исходная реализация  , содержащая   отсчетов, разбивается на   перекрывающихся участков  , где  ,  ;  ;  . Здесь  - параметр (процент) перекрытия. Использование перекрытия особенно целесообразно в тех случаях, когда применяются временные окна с низким уровнем боковых лепестков.

2. На следующем шаге выполняется центрирование сигнала на каждом участке: 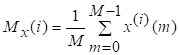 , где   - среднее значение сигнала на i-м участке реализации.

3. Осуществляется взвешивание сигнала функцией окна и рассчитывается энергия окна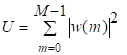

;              ,

где  - весовая функция окна; U- энергия окна.

4. Для каждого участка реализации с использованием алгоритма быстрого преобразования Фурье вычисляется периодограмма и оценка СПМ формируется путем усреднения значений периодограммы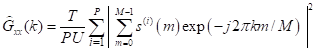

.

5. Оценка взаимного спектра периодограммным методом выглядит следующим образом:

,

где   и  - представляют собой преобразование Фурье на i-м участке реализации от взвешенных с окном последовательностей с нулевым средним.

6.3. Методы анализа, основанные на моделях исследуемых процессов

При моделировании обычными методами предполагается, что корреляция равна нулю за пределами интервала наблюдения. Однако такое предположение неестественно и ограничивает разрешающую способность величиной, приблизитель­но обратно пропорциональной объему выборки данных. Кроме того, резкий переход к нулю вызывает появление больших боковых лепестков в оценке спектра (явление Гиббса). Правильный выбор функции окна может улучшить статистическую стабильность оценки и снизить уровень боковых лепестков, но ценой дальнейшего ухудшения разрешающей способности.

В рассматриваемых методах корреляционная функция продолжается за пределы интервала наблюдения с помощью некоторых рекуррентных соотношений, определяемых параметрами модели. В общем случае в линейной системе с рациональной передаточной функцией связь между входной v и выходной y величинами описывается линейным разностным уравнением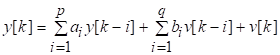

.

Эта модель известна как модель авторегрессии скользящего среднего (АРСС).

Передаточная функция такой системы имеет вид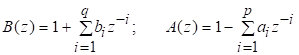

,  .

В том случае, когда входной величиной {v[k]} является белый шум с дисперсией  спектр мощности y представляет собой 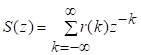 , где  . Функция S(z) является также двухсторонним Z-преобразованием корреляционной функции y[n] в интервале от-¥ до ¥:

.

Если h[n]- импульсная характеристика системы, то H(z-1) является Z-преобразованием инвертированной во времени последовательности h[-n]. Следовательно, если входное воздействие системы H(z) описывается последовательностью s2h[-n], выходная последовательность будет представлять собой корреляционную функцию r(m). Это означает, что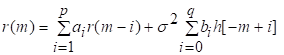

.

Однако, поскольку импульсная характеристика h[n] представляет собой каузальную последовательность, то h[-m+i]=0 для всех m>i. Выражение для корреляционной функции упрощается и принимает вид  .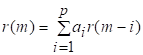

Таким образом, при линейной модели с рациональной передаточной функцией задание p последовательных значений корреляционной функции позволяет однозначно продолжить ее до бесконечности с помощью рекуррентного соотношения.

В том случае, если B(z)=1, то выходная функция формируется как линейная регрессия своих прошлых значений, и поэтому такая модель известна как модель авторегрессии. При k=0 рекуррентное соотношение для корреляционной функции имеет вид 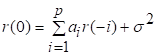 . Задавая M ³ p значений корреляционной функции, можно оценить параметры модели авторегрессии из приведенных рекуррентных уравнений для первых p значений из k. В матричной форме они имеют вид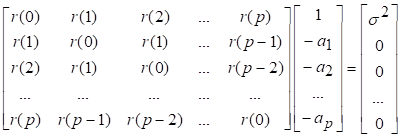

.

Таким образом, параметрическая оценка с использованием модели авторегрессии включает решение линейной системы с симметричной положительно определенной теплицевой матрицей, которое может быть выполнено очень эффективно с помощью алгоритма Левинсона.

Метод максимума энтропии. Основан на предположении, что корреляционная функция экстраполирована так, что энтропия данных, характеризуемая этой функцией, максимальна. Энтропия определяется как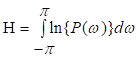

,

где  .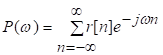

Для того, чтобы найти максимум H, возьмем производную от H по {r(i)}. Это приведет к уравнению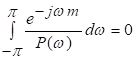

, |m|=N+1, N+2,…,

которое означает, что   определяется рядом Фурье с конечным числом членов, т.е.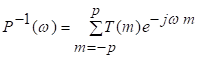

.

Учитывая неотрицательность  , в соответствии с теоремой факторизации спектра получаем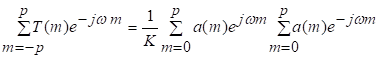

,

при некотором коэффициенте K и множестве значений {a(m)},a(0)=1. Иными словами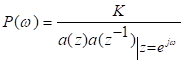

.

Практическое вычисление коэффициентов включает решение уравнения для авторегрессии.

Метод Писаренко. Предложен для решения задачи выделения синусоидальных сигналов в белом шуме. Предположим, что имеется p комплексных экспоненциальных составляющих с амплитудами {qi, i=1, 2,…, p} и частотами {wi, i=1, 2, …, p} в смеси с некоррелированным белым шумом. Тогда теплицева матрица, образованная точными значениями корреляционной функции, в идеальном случае должна иметь следующий вид

R=Rx +Rn=FAF*T+s2I,

где Rx – ковариационная матрица сигнала, Rn – ковариационная матрица шума, знак *Т означает транспонирование с переходом к комплексно-сопряженным величинам: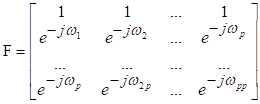

,         .

Заметим, что для данной модели матрица FAF*T имеет ранг p, и поэтому значение s2 должно быть собственным значением матрицы R. Корни, связанные с собственным вектором, соответствующим s2, будут равны  .

Алгоритм метода Писаренко.

1)    вычислить наименьшее собственное значение матрицы R;

2)    вычислить соответствующий собственный вектор a;

3)    определить местоположение спектральных линий, решая уравнение a(z)=0;

4)    определить мощность каждой синусоидальной составляющей решая матричное уравнение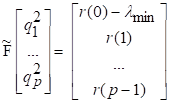

,

где  получается из матрицы F исключением последней строки.

 Если число синусоидальных сигналов заранее неизвестно, то исследование можно начинать с теплицевой матрицы размером N´N и нахождения распределения ее собственных значений. В идеальном случае наименьшее собственное значение будет иметь кратность (N-p), а p можно оценить из распределения собственных значений. Если в окрестности наименьшего собственного значения имеется множество собственных значений, а не одно кратное наименьшее значение, то применение метода Писаренко невозможно. Тогда необходимо обращаться к таким методам, как MUSIC или методу теплицевой аппроксимации на основе сингулярного разложения. Суть последнего метода состоит в том, что для нахождения характеристик прогнозирующего фильтра определяются собственные векторы матрицы R, соответствующие наибольшим собственным значениям, а не наименьшему, и затем вычисляются частоты синусоидальных составляющих.

Метод теплицевой аппроксимации. При использовании метода  первый шаг состоит в получении оценки ковариационной матрицы R, которая в общем случае имеет полный ранг. Это достигается сингулярным разложением следующего вида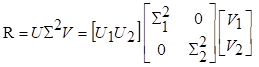

,

где S1-(p´p) – матрица;  S2-(N-p)´ (N-p) – матрица.

Ещё посмотрите лекцию "4.1. Мультипрограммирование" по этой теме.

В присутствии белого шума сингулярные значения изменяются, несмотря на то, что сингулярные вектора остаются неизменными. Фактически все сингулярные значения увеличиваются на величину, равную дисперсии шума, и поэтому самое малое сингулярное значение можно вычесть, чтобы скомпенсировать этот эффект, т.е.

,

где   - самое малое сингулярное значение матрицы R.

Далее определяют так называемую матрицу наблюдаемости  , при этом  . Второй шаг включает определение параметров модели сигнала. Используя  метод наименьших квадратов, получают матрицу  , где знак t - означает псевдообращение матрицы, а знак ­-означает, что матрица получена смещением исходной матрицы на одну строку вверх.

Собственные значения матрица F определяют частоты синусоидальных сигналов.