81. Статистические методы, фильтрация и анализ спектров
 Скачать 0.98 Mb. Скачать 0.98 Mb.
|
82. Адаптивные модели и методы прогнозирования. Особенности адаптивных моделей, их виды, методы построенияАдаптивные модели прогнозирования — это модели дисконтирования данных, способные быстро приспосабливать свою структуру и параметры к изменению условий. Инструментом прогноза в адаптивных моделях, как и в кривых роста, является математическая модель с единственным фактором «время». При оценке параметров адаптивных моделей (в отличие от рассматриваемых ранее моделей «кривых роста») наблюдениям (уровням ряда) присваиваются различные веса в зависимости от того, насколько сильным признается их влияние на текущий уровень. Это позволяет учитывать изменения в тенденции, а также любые колебания, в которых прослеживается закономерность. Все адаптивные модели базируются на двух схемах: • скользящей средней (СС-модели); • авторегрессии (АР-модели). Согласно схеме скользящей средней оценкой текущего уровня является взвешенная средняя всех предшествующих уровней, причем веса при наблюдениях убывают по мере удаления от последнего уровня, т.е. информационная ценность наблюдений признается тем большей, чем ближе они к концу интервала наблюдений. Реакция на ошибку прогноза и дисконтирование уровней временного ряда в моделях, базирующихся на схеме СС, определяется с помощью параметров сглаживания (адаптации), значения которых могут изменяться от 0 до 1. Высокое значение этих параметров означает придание большего веса последним уровням ряда, а низкое — предшествующим наблюдениям. В авторегрессионной схеме оценкой текущего уровня служит взвешенная сумма не всех, а нескольких предшествующих уровней, при этом весовые коэффициенты при наблюдениях не ранжированы. Информационная ценность наблюдений определяется не их близостью к моделируемому уровню, а теснотой связи между ними. В практике статистического прогнозирования наиболее часто используются две базовые СС-модели — Брауна и Хольта, первая из них является частным случаем второй. Эти модели представляют процесс развития как линейную тенденцию с постоянно изменяющимися параметрами. 1. Метод Брауна, основанный на экспоненциальном сглаживании, был предложен для получения прогнозов различных экономических параметров. Он широко применяется при прогнозировании макро- и микроэкономических параметров экономических систем, в том числе торговых. Позволяет получить хороший прогноз тренда для коротких рядов с постоянным трендом. Достаточно часто используется для прогноза продаж различных пищевых продуктов. Модель Брауна может отображать развитие не только в виде линейной тенденции, но и в виде случайного процесса, не имеющего тенденции, а также в виде параболической тенденции. В связи с этим различают модели Брауна: • нулевого порядка — описывают процессы, не имеющие тенденции развития. Модель имеет лишь один параметр а0(оценка текущего уровня). Прогноз развития на т шагов вперед осуществляется по формуле у(+х= aQ. Такая модель еще называется «наивной» («будет, как было»). Доверительный интервал прогноза получают по формуле [10] • первого порядка — отражают развитие в виде линейной тенденции. Модель имеет два параметра: я0 — значение, близкое к последнему уровню, представляет как бы закономерную составляющую этого уровня; а{ определяет прирост, сформировавшийся в основном к концу периода наблюдений, но отражающий также (правда, в меньшей степени) скорость роста на более ранних этапах. Прогноз получают по формуле ут = а0+ я,т, а доверительный интервал прогноза — по формуле [10] 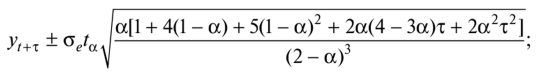 • второго порядка — отражают развитие в виде параболической тенденции с изменяющимися «скоростью» и «ускорением». Модель имеет три параметра (а2— оценка текущего прироста, или «ускорение»). Прогноз осуществляется по формуле ут = а0 + а ,т + я2т2. 2. Метод Хольта был разработан как модификация метода Брауна для учета линейности тренда изучаемой величины [27]. Эта особенность метода определила значительную широту его применения, главным образом для экономических показателей торгового процесса. Традиционно метод применяют при прогнозировании с ярко выраженной тенденцией на повышение или понижение. Так, метод используют при прогнозировании величины выручки в супермаркетах в течение одного квартала, прогнозировании продаж вина в предпраздничные или послепразд- ничные дни. Общая схема построения адаптивных моделей: • По нескольким первым наблюдениям ряда оцениваются значения параметров модели. • По имеющейся модели дается прогноз на один шаг, причем его отклонение от фактических значений ряда расценивается как ошибка прогнозирования, которая учитывается в соответствии с принятой схемой корректировки параметров модели. • По модели со скорректированными параметрами рассчитывается прогнозная оценка на следующий момент времени, и весь процесс повторяется вновь до исчерпания фактических членов ряда. Таким образом, модель постоянно «впитывает» новую информацию, адаптируется к ней и к концу периода отражает тенденцию развития. • Прогнозирование на будущее осуществляется с использованием параметров, определенных на последнем шаге по последним фактическим наблюдениям ряда. Рассмотрим этапы построения линейной адаптивной модели Брауна двумя способами, связанными с различными представлениями формул. Первый способ 1. По первым пяти точкам временного ряда оценивают значения а0 и я, параметров модели с помощью метода наименьших квадратов для линейной аппроксимации по формулам (3.3.5): 2. С использованием параметров а0 и а{, которые соответствуют нулевому моменту времени, по модели Брауна делают прогноз на первый шаг (т= 1): 3. Расчетное значение j>, показателя сравнивают с фактическим значением у{ и находят величину отклонения е}: Для остальных членов ряда отклонение (остаточная компонента) находится по формуле = у- y(t); его используют для корректировки параметров модели в соответствии с принятой схемой. 4. Корректируют параметры модели а0(() и ащ по следующим формулам: 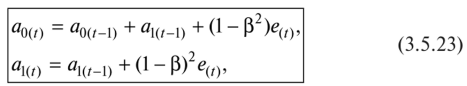 где (3 — коэффициент дисконтирования данных, отражающий большую степень доверия более поздним наблюдениям; 1 — р = ос — параметр сглаживания. Оптимальное значение (3 находят итеративным путем, т.е. многократным построением модели при разных значениях (3 и выбором наилучшей. Параметры вычисляют последовательно, от уровня к уровню, и их значения для последнего уровня определяют окончательный вид модели. 5. По модели со скорректированными параметрами а0,() и о1(() находят прогноз на следующий момент времени (т = 1): 6. Возврат к пункту 3, если t < п. Если t - п, то построенную модель можно использовать для прогнозирования на будущее. Точечный прогноз рассчитывают по формуле Второй способ 1. По первым пяти точкам временного ряда оценивают значения а0 и «j параметров модели с помощью метода наименьших квадратов для линейной аппроксимации: 2. С использованием параметров а0 и аь которые соответствуют моменту времени / = 0, вычисляют начальные условия экспоненциальных средних: 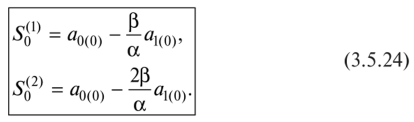 3. С учетом выбранного значения параметра сглаживания а или коэффициента дисконтирования |3 (а+ (3 = 1) вычисляют значения экспоненциальных средних: 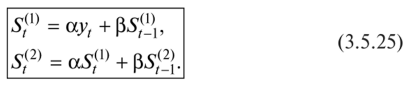 4. Корректируют параметры модели я0(/) и а1(/) по следующим формулам: 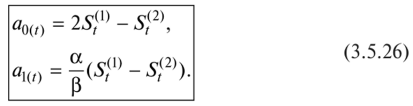 5. По модели со скорректированными параметрами а0(/) и а1(() находят прогноз на следующий момент времени: 6. Возврат к пункту 3, если t < п. Если t = п, то построенную модель можно использовать для прогнозирования на будущее. Точечный прогноз рассчитывают по формуле Пример 3.5.5. По имеющейся информации (yt в табл. 3.5.14) об объемах продаж нового товара (тыс. руб.) в течение 35 недель построить адаптивную модель Брауна с линейной тенденцией (двумя способами). Построить прогноз на три шага вперед, используя оптимальное значение параметра сглаживания. Результаты моделирования и прогнозирования привести на графике. Таблица 3.5.14
Решение Первый способ 1. По первым пяти точкам временного ряда оцениваем значения а0 и ах параметров модели с помощью МНК для линейной аппроксимации: Получаем начальные значения параметров модели а0= 16,68 и ах= 10,48, которые соответствуют моменту времени t = 0. 2. Находим прогноз на первый шаг: 3. Находим величину отклонения е{=у{- ух = 27,3 - 27,16 = 0,14. Все расчеты в табл. 3.5.15 показаны для а = 0,3; |3 = 0,7. 4. Корректируем параметры модели о0(/) и aX{t) (/ = 1): 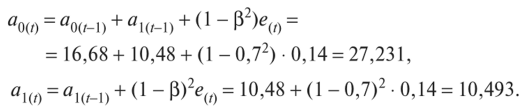 5. Находим прогноз на следующий момент времени (/=2): 6. Возвращаемся к пункту 3, вычисления повторяем до конца наблюдений. 7. Параметры модели, полученные в последний момент времени (/=35), используем для построения прогноза (т = 1, 2, 3):  Таблица 3.5.15
Второй способ 1. По первым пяти точкам временного ряда оцениваем значения а0 и ах параметров модели с помощью МНК для линейной аппроксимации: Получаем начальные значения параметров модели я0 = 16,68 и щ = 10,48, которые соответствуют моменту времени /= 0. Все расчеты в табл. 3.5.16 показаны для а = 0,3; р = 0,7. 2. Вычисляем начальные условия экспоненциальных средних: Таблица 3.5.16
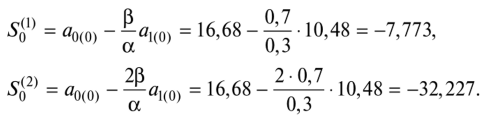 3. С учетом выбранного значения параметра сглаживания а или коэффициента дисконтирования (3 (а + (3 = 1) вычисляем значения экспоненциальных средних (/ = 1): 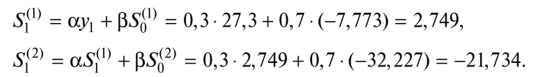 4. Корректируем параметры модели я0(/) и а[1] Таблица 3.5.19
Определение наличия во временном ряде тренда.Решение данной задачи можно осуществить иливизуально —путем нанесения на график соответствующего исходного временного ряда, илианалитическими методами,изложенными в подпараграфе 3.5.2. При использовании визуального метода можно либо последовательно наносить на график все уровни тренд-сезонного временного ряда (рис. 3.5.20,а),либо для каждого года строить отдельную кривую (рис. 3.5.20,б),причем если тренд возрастающий или убывающий, то кривые, соответствующие каждому году, будут располагаться друг над другом. 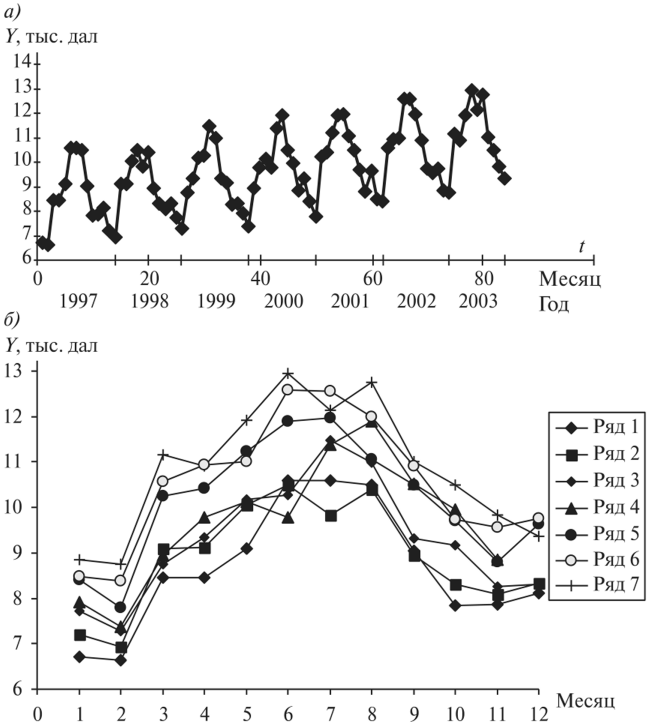 Рис. 3.5.20.Графики тренд-сезонного временного ряда, представленного в табл. 3.5.19 Для определения наличия во временном ряде сезонных колебаний рекомендуется использовать следующие критерии: • дисперсионный; • гармонический (в данной работе не рассматривается); • критерий, основанный на сравнении распределения коэффициента автокорреляции с распределением циклического коэффициента автокорреляции. Смысл их применения сводится кпроверке на случайность остаточной компоненты,остающейся после выделения из исходного временного ряда тренда. При применениидисперсионного критериявыдвигается гипотеза о том, что во временном ряде, из которого отфильтрован тренд, отсутствуют сезонные колебания. В случае справедливости данной гипотезы /’-статистика будет иметь /’-распределение с (Г0- 1) и(п -Г0) степенями свободы: 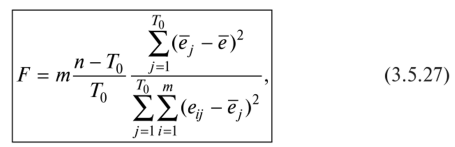 где 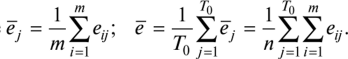 Здесь используются следующие обозначения:е— значения остаточного ряда после выделения из него тренда, i =1,т; j =1, /0;т —число лет наблюдений; Г0— период колебаний (Г0= 4 для ряда квартальных данных,Т0=12 для ряда месячных данных);п —количество наблюдений во временном ряде,п = тТ0. Для обнаружения сезонных колебаний с использованиемкоэффициента автокорреляцииего значения рассчитываются по формуле 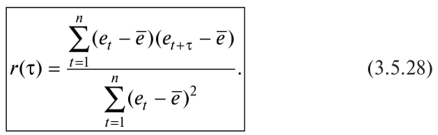 Расчетные значения коэффициентов автокорреляции сравниваются с табличными значениями с заданным уровнем значимости, и в случае когдарасчетноезначение большетабличного,соответствующий коэффициент признается значимым, что может свидетельствовать о наличии сезонных колебаний. Автокоррелированность остаточного ряда может быть также проверена по критерию Дарбина — Уотсона [см. формулу (3.4.8)]. Для большей наглядности отсутствия или наличия сезонных колебаний рекомендуется строить график автокорреляционной функции остаточного временного ряда (см., например, рис. 3.5.23). Фильтрация компонент тренд-сезонного временного ряда.Разделение тренд-сезонного временного ряда на компоненты можно осуществлятьрегрессионными, спектральнымииитерационнымиметодами. В экономических исследованиях чаще используют итерационные методы, которые отличает простота и приемлемая точность фильтрации. Выбор конкретного итерационного метода определяется предположением о том, какая существует зависимость между компонентами тренд-сезонного временного ряда — аддитивная или мультипликативная, а также зависит от требуемой точности определения компонент. Принято считать, что аддитивное соотношение между компонентами тренд-сезонного временного ряда имеет место в том случае, когда с течением времени сезонная компонента существенноне изменяется.В тех случаях, когда сезонная составляющая из года в годвозрастаетилиснижается,используют мультипликативное соотношение. Рассмотрималгоритм фильтрацииодного из итерационных методов, предположив наличие аддитивной взаимосвязи между компонентами ряда, т.е. 1.Сглаживаем исходный временной ряд методом центрированной скользящей средней,используя весовые коэффициенты: • 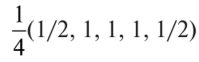 для квартальных данных; для квартальных данных;• 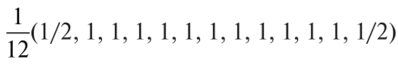 для месячных данных, т.е. по формуле для месячных данных, т.е. по формуле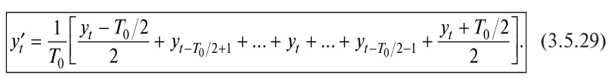 В результате получаем временной ряд, являющийся предварительным значением тренда. 2.Из исходного временного ряда вычитаем сглаженные значения: Полученный ряд содержит сезонную и случайную компоненты. 3.Усредняем полученные значения еза все года по каждому месяцу (кварталу): 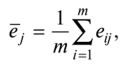 где ёу — сезонная компонента, «невыправленная» сезонная волна. 4.Корректируем средние значения ёрувеличивая или уменьшая их на одно и то же число так, чтобы их сумма была равна нулю, — получим «выправленную» сезонную волну. Корректирующее число рассчитывается следующим образом: сумма оценок сезонных компонент делится на 12 (при месячных данных) или на 4 (при квартальных данных). На эту величину корректируется среднее значениеё,за каждый месяц (квартал) так, чтобы их сумма равнялась нулю. Получим Sj —сезонную волну, т.е. значения сезонной компоненты для каждого месяца (квартала). 5.Проводим десезонализацию исходных данных: вычитаем соответствующие значения сезонной компоненты из фактических значений ряда за каждый месяц (квартал), т.е. Вычисленные таким образом значения ряда состоят из тренда и случайной компоненты. 6.Подбираем для полученного ряда кривую роста, аппроксимирующую тренд. Находим параметры уравнения кривой и подставляем в него последовательно значения /. Полученные оценки (обозначим их через у'.) и будут являться значениями тренда. 7. Определяем значения случайной компоненты: которые можно использовать для определения точности и адекватности систематических компонент — тренда и сезонной волны. 8.Осуществляем прогнозирование тренд-сезонного экономического процессапутем сложения (для аддитивной модели) значений тренда, рассчитанных по уравнению тренда для каждого момента времени прогнозного периода, с соответствующим месячным (квартальным) значением сезонной компоненты: 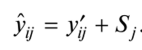 Алгоритм фильтрации при принятии гипотезы о мультипликативной взаимосвязи между компонентами тренд-сезонного экономического процесса, т.е. остается тот же, что и при аддитивной взаимосвязи, изменяются только формулы в пунктах 2, 4, 5, 7, 8. Они будут следующими: 2.Делим значения исходного временного ряда на соответствующие сглаженные значения ряда: 4.Корректируем средние значения сезонных компонентза каждый месяц (квартал) так, чтобы их сумма, деленная на 12 (месячные наблюдения) или на 4 (квартальные наблюдения), равнялась единице. 5.Проводим десезонализацию исходных данных:исходные уровни временного ряда делим на соответствующие скорректированные значения сезонной волны, т.е. 7. Определяем значения случайной компоненты: 8.Осуществляем прогнозирование тренд-сезонного экономического процессапутем умножения (для мультипликативной модели) значений тренда, рассчитанных по уравнению тренда для каждого момента прогнозного периода, на соответствующие месячные (квартальные) значения сезонной компоненты: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
