диплом. Диплом. Развитие общества невозможно без использования энергии. Масштабы энергопотребления за несколько тысячелетий возросли до громадных величин. Потребность в энергии резко повышается с техническим и культурным прогрессом

Название	Развитие общества невозможно без использования энергии. Масштабы энергопотребления за несколько тысячелетий возросли до громадных величин. Потребность в энергии резко повышается с техническим и культурным прогрессом
Анкор	диплом
Дата	23.05.2023
Размер	1.35 Mb.
Формат файла
Имя файла	Диплом.docx
Тип	Документы #1155186
страница	2 из 5

1 2 3 4 5

, (1.25)

где x_2пр- приведенное индуктивное сопротивление рассеяния обмотки бегуна

x_2пр = x₁λ_2пр/ λ₁, (1.26)

x_2пр= 0,022 Ом;
z_2пр = 0,246 Ом;

cosѰ₂= r_2пр/Sz_2пр, (1.27)

cosѰ₂= 0,996.

Вычисляется скорость бегущего поля индуктора:

V₁ = 2f₁τ₁ , (1.28)

V₁ = 0,067 м/с.

Находится электромагнитная мощность, передающаяся из индуктора в бегун в пусковом режиме:

Р_12п= F_пV₁, (1.29)

Р_12п= 1,173х10³Вт.

Определяется приведённый ток короткозамкнутой обмотки бегуна в пусковом режиме:

I₂_ппр =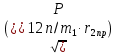

, (1.30)

I_2ппр = 39,986 А.

Вычисляется ЭДС обмотки индуктора Е₁=Е_2п:

Е₁ = Р_12п/m₁I_2ппрcosѰ₂, (1.31)

Е₁ = 9,822 В.

Находится магнитная индукция в воздушном зазоре:

B_δ = Е₁/4,44f₁W_1э²D₁τ₁, (1.32)

B_δ = 1,724 Тл.

_{Определяется магнитодвижущая сила воздушного зазора:}

F_δ= 2δk_δB_δ/μ₀ , (1.33)

F_δ= 8,851 x10³А.

Вычисляется магнитный поток в зазоре:

Ф_δ = 2B_δ τ₁D₁, (1.34)

Ф_δ = 0,026 Вб.

Находится индукция в зубце индуктора:

В_з1 = B_δ t₁/b_з1k_ст , (1.35)

где k_ст=0,93 – коэффициент заполнения зубца индуктора сталью;

В_з1 = 5,563 Тл.

_{Выбирается марка и толщина листа стали для зубцов и сердечников индуктора и бегуна. Определяется напряжённость магнитного поля в зубцах и спинках индуктора и бегуна по кривым намагничивания стали.}

Зубцы индуктора и бегуна и сердечник индуктора изготавливаются из стали 2013 с толщиной листа 0,5 мм. Для сердечника бегуна применяется заготовка из стали Ст10.

Намагниченность магнитного поля в зубце индуктора для стали 2013 при В_з1=5,563Тл: Н_з1=188А/м.

Вычисляется МДС зубцов индуктора:

F_з1= 2H_з1h_з1, (1.36)

где h_з1= h_п1= 5 см;

F_з1= 18,8 А.

Вычисляется индукция в спинке индуктора:

B_сп1=0.5 Ф_δ k_σп/h_сп1πD_сп1k_смk_зсп, (1.37)

гдеk_σп =1,2 – коэффициент рассеяния потока;

k_зсп=0,9 - коэффициент, учитывающий конструкцию индуктора ЛАД и зависящий от количества сердечников в индукторе;

D_сп1–средний диаметр спинки индуктора:

D_сп1= D₁+2h_п1+h_сп1, (1.38)

D_сп1= 21,3 см.

B_сп1= 0,92 Тл.

Определяется напряжённость магнитного поля в спинке индуктора для B_сп1=0,92 Tл: Н_сп1=210 А/м

Вычисляется МДС спинки индуктора:

F_сп1 = Н_сп1τ₁, (1.39)

F_сп1 = 18,9 A.

Находится индукция в зубцах бегуна:

B_з2= B_бt₂/b_з2k_ст , (1.40)

B_з2= 6,675 Тл.

Определяется напряжённость магнитного поля в зубце бегуна для стали 2013 при B_з2=6,675 Т: Н_з2=241 А/м.

Определяется МДС зубцов бегуна:

F_з2 = 2Н_з2h_з2, (1.41)

где h_з2= h_п2;

F_з2 = 12,05 А.

Вычисляется индукция в спинке бегуна:

В_сп2 = 2Ф_б/π(D_в²D₀²) , (1.42)

где

D_в= D₂ – h_з2, (1.43)

D_в= 3 см.

D₀ примем равным 0 м, т.е. сердечник бегуна – цельный;

В_сп2 = 18,224 Тл.

Определяется напряжённость магнитного поля в спинке бегуна для литой стали при В_сп2=2,223 Тл: Н_сп2=232 А/м

Вычисляется МДС спинки бегуна:

F_сп2 = H_сп2τ₁ , (1.44)

F_сп2 = 20,88 А.

Находится суммарная МДС:

F_μ= F_б+F_з1+F_сп1+F_з2+F_сп2, (1.45)

F_μ= 8,922х10³ А.

Определяется коэффициент насыщения:

k_нас = F_μ /F_б, (1.46)

k_нас = 1,008.

Таблица 1.4 – Расчет массы зубцов и сердечника

Наименование	Формулы	Ответ
Масса зубцов индуктора, кг	m_з1 = Z₁b₁h₁l_ксрρ_ст	29,332
Масса зубцов бегуна, кг	m_з2 = Z₂πb_з2 (D₂²-D_в²)ρ_ст/4	5,054
Масса сердечника индуктора, кг	m_сп1 = h_сп1πl₁D_сп1ρ_стk_зап	76,099
Масса сердечника бегуна (в пределах активной зоны), кг	m_сп2 = π(D_в²– D₀²)l₁ρ_стk_ст	2,977

где ρ_ст= 7800 кг/м³- удельная масса стали;

k_ст=1– т.к. сердечник бегуна цельнометаллический (не шихтованный).

Таблица 1.5 – Расчет потерь в стали

Наименование	Формулы	Ответ
Потери в стали спинки индуктора, Вт	Р_стс1= Р_1.0/50(f₁/50)^1,5k_дсB_сп1²m_сп1	0,164
Потери в стали сердечника бегуна, Вт	Р_стс2= Р_1.0/50(f₁/50)^1,5k_дс B_сп2²m_сп2	2,521
Потери в стали в зубцах индуктора, Вт	Р_стз1= Р_1.0/50(f₁/50)^1,5k_дзB_з1²m_з1	2,604
Потери в стали зубцов бегуна, Вт	Р_стз2= Р_1.0/50(f₁/50)^1,5k_дсB_з2²m_з2	0,646
Основные потери в стали	Р_ст= Р_стз1+Р_стс1+Р_стз2+Р_стс2	5,936

где Р_1.0/50=2,5 Вт/кг - удельные потери в стали 2013 толщиной 0,5 мм при индукции В=1Тл и частоте перемагничивания f=50 Гц;

k_д- коэффициент, учитывающий влияние на потери в стали неравномерности распределения потока по сечениям участков магнитопровода и технологических факторов. Для машин мощностью меньше 250 кВт можно принять k_дз=1,8 (для зубцов) и k_дс=1,6 (для сердечников). Для расчёта потерь в стали учитывается масса тех зубцов бегуна, которые находятся в пределах активной зоны индуктора.

Вычисляется намагничивающий ток:

I_μ= pF_μ/F_б, (1.47)

I_μ = 42,758 А.

Находится активная составляющая тока холостого хода:

I_0а= Р_ст/m₁E₁ , (1.48)

I_0а= 0,201 А.

Рассчитываются параметры схемы замещения:

r₁₂= P_cm/m₁I₀_а², (1.49)

r₁₂ = 48,76 Ом.

I₀_р = I_μ.

x₁₂ = E₁/ I₀_р, (1.50)

x₁₂ = 0,23 Ом.

z₁₂ =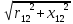

, (1.51)

z₁₂ = 48,76Ом.

r₀= r₁₂x₁₂²/z₁₂², (1.52)

r₀= 1.08210^-3Ом.

x₀= x₁₂r₁₂²/z₁²₂, (1.53)

x₀= 0,23 Ом.

Комплексный коэффициент C`₁рассчитывается приближённо: C`₁=C₁:

C₁= 1+x₁/x₀ , (1.54)

C₁= 1,22.

Находится ток в фазе обмотки индуктора:

I₁=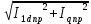

, (1.55)

где

I_1d_пр= I₀_а+I₂_ппрcosѰ₂, (1.56)

I_1d_пр= 40,021 А.

I_1q_пр= I_0p+I₂_ппрsinѰ₂, (1.57)

I_1q_пр= 46,404 А.

sinѰ₂= x₂_пр/z₂_пр, (1.58)

sinѰ₂= 0,091.

I₁= 61,278 А.

Вычисляются электрические потери в обмотке индуктора

Р_э1= m₁I₁²r₁, (1.59)

Р_э1=5,025х10³Вт.

Вычисляются электрические потери в короткозамкнутой обмотке бегуна:

Р_э2 = m₁I_2ппр²r_2пр, (1.60)

Р_э2 = 1,173х10³Вт.

Определяется потребляемая мощность:

P₁ = P₁₂+ P_э1+P_э2 , (1.61)

где P₁₂ = Р_ст

P₁ = 6,205х10³ Вт.

Вычисляется фазное напряжение обмотки индуктора:

_{, (1.62)}

U₁ = 35,358 В.

Определяется пусковая сила: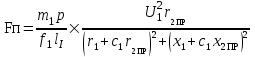

, (1.63)

F_п = 2,455x10⁴ Н.

Определяется cos :

cos = Р₁/m₁U₁I₁, (1.64)

cos = 0,955.

Расчёт механической характеристики: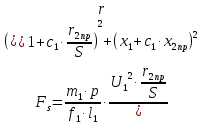

, Н (1.65)

Таблица 1.6 – Механические характеристики

F₁	F_0,9	F_0,8	F_0,7	F_0,6	F_0,5	F_0,4	F_0,3	F_0,2	F_0,1
2,455х10⁴	2,503х10⁴	2,54х10⁴	2,562х10⁴	2,559х10⁴	2,516х10⁴	2,41х10⁴	2,203х10⁴	1,828х10⁴	1,168х10⁴

Номинальное скольжение определяется по механической характеристике двигателя:

S_н=0,5.

Находится номинальная сила: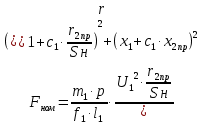

, (1.66)

F_ном = 2,516х10⁴ Н.

Определяется электромагнитная мощность, передающаяся из индуктора в бегун в номинальном режиме:

Р_12ном = F_номV₁ , (1.67)

Р_12ном = 1,667х10⁴ Н.

Вычисляется номинальный приведённый ток короткозамкнутой обмотки бегуна:

I₂_нпр =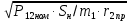

, (1.68)

I_2нпр = 33,804 А.

Находится номинальное полное приведенное сопротивление:

z_2нпр =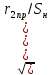

, (1.69)

z_2нпр = 0,49 Ом.

cosѰ_2н= r_2пр/S_нz_2нпр , (1.70)

cosѰ_2н= 0,999.

sinѰ_2н= x_2пр/z_2нпр_{, (1.71)}

sinѰ_2н= 0,046.

Находится номинальный ток в фазе индуктора:

I_1н=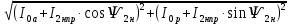

, (1.72)

I_1н= 55,828 А.

Определяются электрические потери в обмотке индуктора в номинальном режиме:

Р_э1н= m₁I_1н²r_2пр, (1.73)

Р_э1н= 2,287х10³ Вт.

Находятся электрические потери в короткозамкнутой обмотке бегуна:

Р_э2н= m₁I_нпр²r_2пр, (1.74)

Р_э2н= 838,555Вт.

Определяется номинальная потребляемая мощность:

Р_1н= Р_12ном+Р_э1н+Р_ст, (1.75)

Р_1н= 3,97х10³ Вт.

Находится полезная механическая мощность в номинальном режиме:

Р_2н= F_номV_ср_{, (1.76)}

Р_2н= 1,677х10³ Вт.

Вычисляется коэффициент полезного действия:

η_н = (Р_2н/Р_1н) 100 , (1.77)

η_н = 42,242.

_{Находится} cos_н_:

cos_н = Р_1н/m₁U₁I_1н, (1.78)

cos_н = 0,67.

Определяется плотность тока в обмотке индуктора в номинальном режиме:

j_н= I_н²/q_пр, (1.79)

j_н = 5,803 А/мм²

Тепловой расчёт линейного двигателя:

_{Выбирается изоляция нагревостойкости класса}_F_.

_{Определяется необходимая площадь радиатора:}

S_р ≥ Р_э1н/(t_доп-t_окр.ср)σ_рас, (1.80)

где σ_рас=0,15– коэффициент теплоотдачи от радиатора в окружающую среду;

t_доп=180˚С– допустимая температура изоляции нагревостойкости класса F;

t_окр.ср= 30˚С– температура окружающей среды.

S_р ≥ 913,2 см².

Вывод: расчётный КПД вышел низкий, значит управление за счёт изменения скольжения неэффективно, следовательно, целесообразно использование статического преобразователя частоты.

Развиваемое усилие соответствует необходимой силе тяги станка.

Выделяемая тепловая энергия отводится за счёт ребристой поверхности двигателя, чтобы двигатель не перегревался.

Плотность тока не превышает рекомендуемой величины 10 А/мм².

Коэффициент заполнения паза удовлетворяет технологическим требования и не превышает величины 0.8, то есть обмотка укладывается в пазы.

Если в результате расчёта, какой-то из этих вышеперечисленных значимых пунктов не выполняется, то расчёт необходимо повторить, изменив конструктивные особенности магнитопровода и обмотки, то есть взять магнитопровод с другими размерами пазов и провод другого сечения/диаметра.

В результате был получен линейный асинхронный двигатель, удовлетворяющий необходимые требования, который конструктивно умещается в станок

1 2 3 4 5