практика. Задача 1 Определить коэффициент полезного действия трехфазного трансформатора (%) со схемой соединения обмоток УУн, мощностью S
 Скачать 0.95 Mb. Скачать 0.95 Mb.
|
|
Трёхфазные цепи Задача №1 Определить коэффициент полезного действия трехфазного трансформатора (%) со схемой соединения обмоток У/Ун, мощностью Sн = 160 кВ×А, номинальное напряжение первичной обмотки U1н = 10 кВ, вторичной обмотки — U2н = 0,4 кВ, ток холостого хода Iх = 2,5%, активное сопротивление первичной обмотки r1 = 6,152 Ом, активное сопротивление намагничивающей ветви схемы замещения rм = 3563 Ом. Трансформатор загружен на 70% номинальной нагрузки и работает при коэффициенте мощности cosj2 = 0,9. В расчете сопротивление первичной обмотки и приведенное сопротивление вторичной обмотки считать одинаковыми. {Ответ с точностью до целого числа.} Решение Коэффициент полезного действия трехфазного трансформатора определится по формуле: 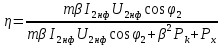 Коэффициент загрузки трансформаторов по условию 70%, в формулу подставляем в относительных единицах b = 0,7. Номинальный ток вторичной стороны трансформатора 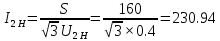 где 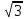 — перевод с линейного напряжения в фазное для схемы «звезда». — перевод с линейного напряжения в фазное для схемы «звезда».Номинальное фазное напряжение вторичной стороны трансформатора Если подставить в формулу (4.5) 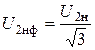 и , получим и , получим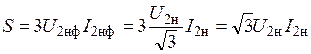 . .Потери короткого замыкания трансформатора можно определить двумя путями (4.6): Удобнее воспользоваться первым уравнением, потому что по условию сопротивление первичной обмотки r1 и приведенное сопротивление вторичной обмотки r´2 считать одинаковыми. Тогда 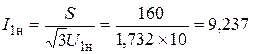 А; А;Ток холостого хода Iх = Iх% ´ I1 = 2,5 ´ 9,237 = 0,2309 А. Потери холостого трансформатора 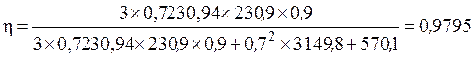 . .Ответ: h = 98%. Задача №2 Определить индуктивное сопротивление намагничивающей ветви схемы замещения трехфазного трансформатора (Ом) со схемой соединения обмоток У/Ун, мощностью Sн = 160 кВ×А, номинальное напряжение первичной обмотки U1 = 10 кВ, потери короткого замыкания Рк = 3150 Вт, напряжение короткого замыкания Uк = 5%, потери холостого хода Рх = 570 Вт, ток холостого хода Iх = 2,5%. В расчете сопротивление первичной обмотки и приведенное сопротивление вторичной обмотки считать одинаковыми, при их расчете намагничивающим током пренебречь. {Ответ с точностью до целого числа.} Решение Индуктивное сопротивление намагничивающей ветви хм определяется по данным опыта холостого хода. Схема замещения трансформатора в режиме холостого хода приведена на рисунке 4.2. 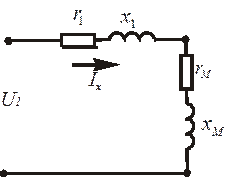 Рисунок 4.2 Схема замещения трансформатора в режиме холостого хода Сопротивления намагничивающей ветви: 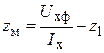 ; ; Ток холостого хода 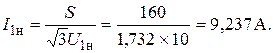 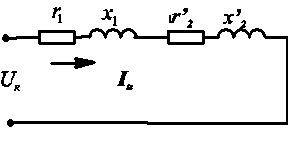 Полное сопротивление первичной обмотки z1, определяется по данным опыта короткого замыкания. Упрощенная схема замещения трансформатора (намагничивающим током пренебрегаем) в режиме короткого замыкания приведена на рисунке 4.3. Полное сопротивление первичной обмотки z1, определяется по данным опыта короткого замыкания. Упрощенная схема замещения трансформатора (намагничивающим током пренебрегаем) в режиме короткого замыкания приведена на рисунке 4.3.Рисунок 4.3 Упрощенная схема замещения трансформатора в режиме короткого замыкания При построении схемы замещения намагничивающим током пренебрегли. 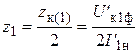 , ,где 2 учитывает, что сопротивление первичной обмотки и приведенное сопротивление вторичной обмотки одинаково (согласно условию). Фазное напряжение короткого замыкания трансформатора 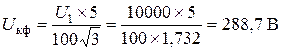 ; ; 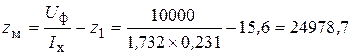 Ом. Ом.Активное сопротивление намагничивающей ветви 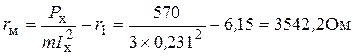 , ,где r1 — активное сопротивление первичной обмотки, 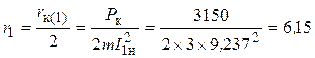 Ом. Ом.Ответ: хм = 24725 Ом. Задача №3 Два трехфазных трансформатора мощностью Sн = 400 кВ·А включили параллельно. Номинальное напряжение первичных обмоток U1 = 10 кВ, коэффициент трансформации Кт = 25. Определить значение уравнительного тока (А), если один из трансформаторов был с нулевой группой соединения обмоток (У/Ун — 0 гр.), а второй — с четвертой (У/Ун — 4 гр). Напряжение короткого замыкания трансформаторов одинаково: Uк = 5%. Сопротивлением соединительных проводов пренебречь. {Ответ с точностью до целого числа.} Решение На рисунке 4.4 показаны векторные диаграммы вторичных напряжений трансформатора с нулевой и четвертой группой соединения обмоток. 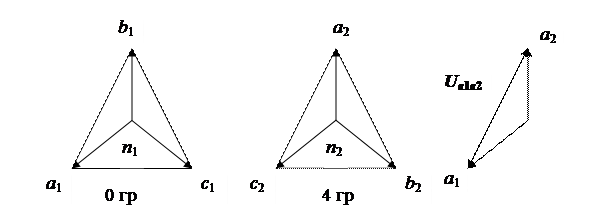 Рисунок 4.4 Векторные диаграммы вторичных напряжений трансформатора При соединении нейтралей трансформаторов n1 и n2 одноименные вводы трансформаторов (например, а1 и а2) попадут под напряжение Uа1а2, значение которого определится по рисунку: Уравнительный ток определится по формуле: 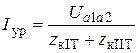 . .Сопротивление короткого замыкания трансформаторов одинаково для обоих трансформаторов: , Напряжение короткого замыкания трансформатора 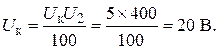 Номинальный ток трансформатора 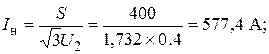 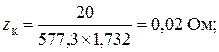 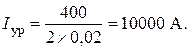 Ответ: = 10000 А. Задача №4 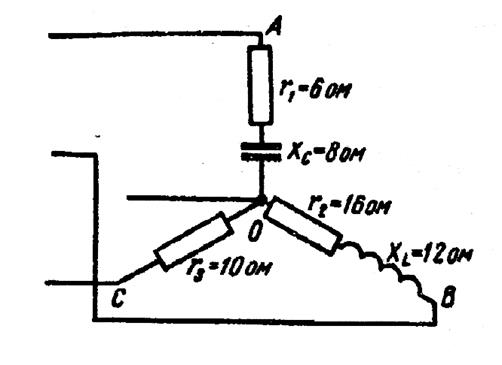 В каждую фазу трехфазной четырехпроводной сети включили сопротивления так, как показано на рис. 6. Величины сопротивлений даны на рисунке. Линейное напряжение сети U=380B. Определить: линейные токи, углы сдвига фаз, ток в нулевом проводе, активную, реактивную и полную мощности трех фаз. Построить в масштабе векторную диаграмму. Решение. 1. Полные сопротивления фаз: 2. Углы сдвига фаз: 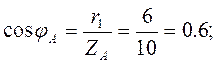 (опережающий); (опережающий);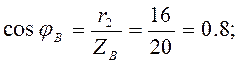 (отстающий); (отстающий);3. Фазное напряжение 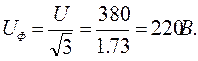 4. Линейные (фазные) токи: 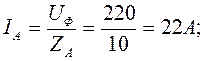 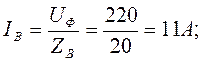 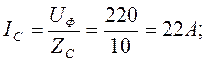 5. Активная мощность потребляется только активными сопротивлениями. Поэтому активная мощность трех фаз 6. Реактивная мощность потребляется только реактивными сопротивлениями. Поэтому реактивная мощность трех фаз Знак «минус» показывает, что реактивная мощность системы носит емкостный характер. 7. Полная мощность трех фаз: 8. Построение векторной диаграммы начинаем с векторов фазных напряжений. 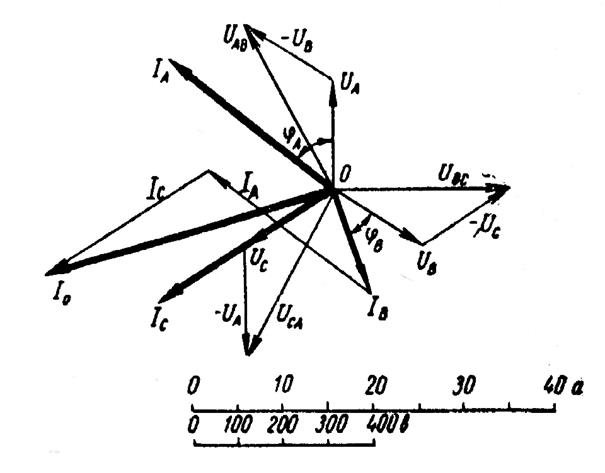 Рис. 7. Из точки О (рис. 7) в принятом масштабе напряжений проводим три вектора фазных напряжений , и , углы между которыми составляют 120°. Затем строим векторы линейных напряжений , и , согласно уравнениям: = – = +(- ); = – = +(- ); = – = +(- ) Черточки над буквами показывают, что векторы должны вычитаться и складываться геометрически. Например, для построения линейного напряжения к вектору нужно геометрически прибавить обратный по направлению вектор . Под углом φА=53° в сторону опережения вектора фазного напряжения откладываем в принятом масштабе токов вектор тока ; под углом φВ=37° в сторону отставания от вектора фазного напряжения откладываем вектор тока . Вектор тока совпадает по направлению с вектором фазного напряжения так как φС=0. Для определения тока в_нулевом проводе I складываем геометрически векторы токов , и . Из векторной диаграммы, пользуясь масштабом для токов, находим ток I=34A. Задача №5 В каждую фазу трехфазной сети включили сопротивления так, как показано на рис. 8. Величины сопротивлений даны на рисунке3. Линейное напряжение сети U =220B. 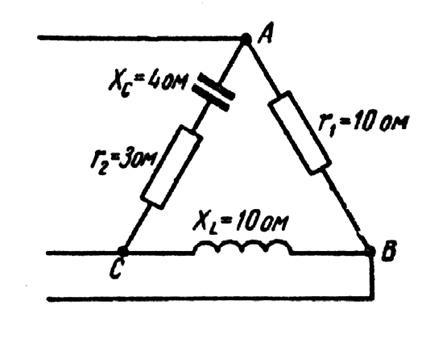 Рис. 8. Определить: фазные и линейные токи, углы сдвига фаз, активную, реактивную и полную мощности трех фаз. Построить в масштабе векторную диаграмму. Решение 1. Полные сопротивления фаз: 2. Углы сдвига фаз: 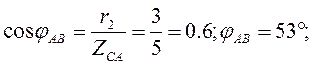 (опережающий). (опережающий).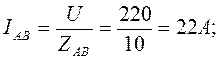 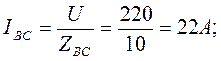 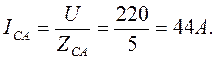 4. Активная мощность потребляется только активными сопротивлениями. Поэтому активная мощность трех фаз 5. Реактивная мощность потребляется только реактивными сопротивлениями. Поэтому реактивная мощность трех фаз 6. Полная мощность трех фаз 7. Для определения линейных токов строим векторную диаграмму (рис. 4). Построение _начинаем с векторов фазных (линейных) напряжений , и . Вектор тока совпадает с вектором фазного напряжения , так как φАВ=0. Вектор тока отстает от вектора на угол φВС =90°, а вектор тока опережает вектор на угол φВС =53° . Линейные токи , и на диаграмме равны геометрической разности соответствующих фазных токов. Например, Из векторной диаграммы графически, пользуясь масштабом, определяем линейные токи: IA=66A; IB=43A; IC=25A.  Puc. 6. Puc. 6.Задача №6 Обмотки трехфазного генератора соединены по схеме “звезда”, э.д.с. в них 220 В. Построить векторные диаграммы и определить линейные напряжения для схемы соединения, в которой в одной точке сходятся: a) X Y Z б) X B Z в) X B C . Начала обмоток – A,B,C, концы обмоток – X,Y,Z. Принять нагрузку на генераторе равной нулю. а) Для данной схемы соединения векторная диаграмма будет выглядеть следующим образом 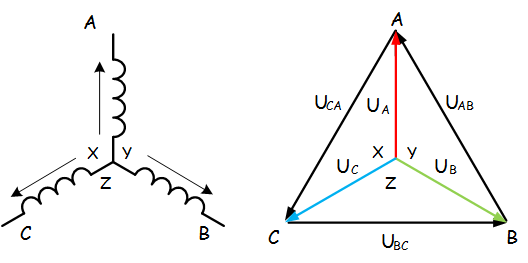 Линейные напряжения в данном случае будут равны и определяться как б) Так как обмотка BY подключена началом в нейтральную точку, то вектор напряжения оказывается повернутым на 180 относительно нормального положения. 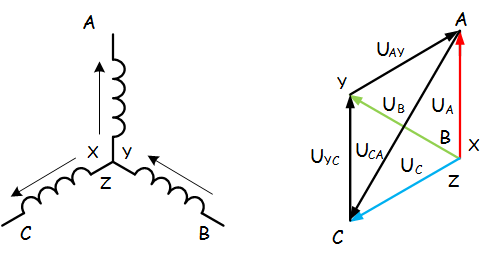 Линейные напряжения в данном примере будут разными по значению 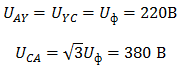 в) В данном случае относительно нормального положения повернуты вектора двух обмоток – BY и CZ. 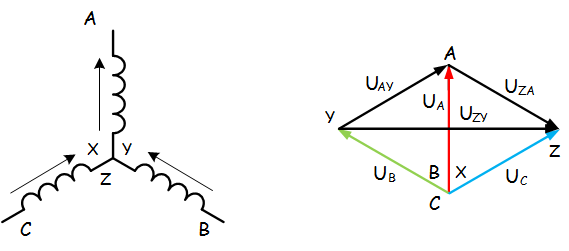 Как и в предыдущем примере, линейные напряжения не будут равны 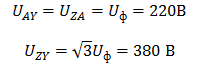 |
