практика. Задача 1 Определить коэффициент полезного действия трехфазного трансформатора (%) со схемой соединения обмоток УУн, мощностью S

• Название: Задача 1 Определить коэффициент полезного действия трехфазного трансформатора (%) со схемой соединения обмоток УУн, мощностью S
• Дата: 03.06.2022
• Размер: 0.95 Mb.
• Имя файла: практика.docx
• Тип: Задача; #568184
• страница: 2 из 4

Задача №7

К зажимам приемника подсоединён трехфазный генератор, как показано на схеме. Определить показания амперметров A₁,A₂ и фазные токи зная, что U_л=380В, R=50 Ом, x_L=35 Ом.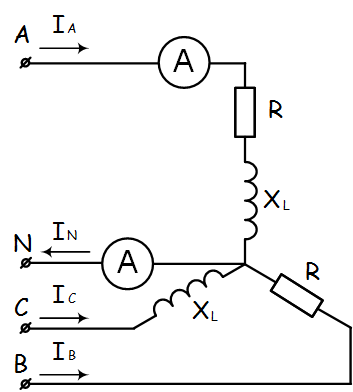



Определим комплексные значения сопротивления (для удобства вычислений будем переводить в показательную форму)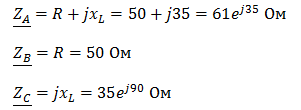



Напряжения в фазах будет равно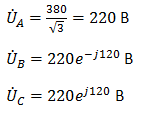



Токи в фазах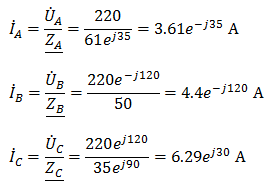

Ток в нейтральном проводе равен (для удобства сложения сначала переведем из показательной формы в алгебраическую, а затем наоборот)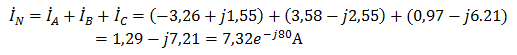



Соответственно, показания амперметров будут следующими: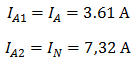



К зажимам приемника, подсоединён трехфазный генератор, обмотки которого соединены по схеме “треугольник”. Определить фазные и линейные токи, показания вольтметра, зная, что линейное напряжение равно 220 В, R=25 Ом, x_L=x_C=10 Ом.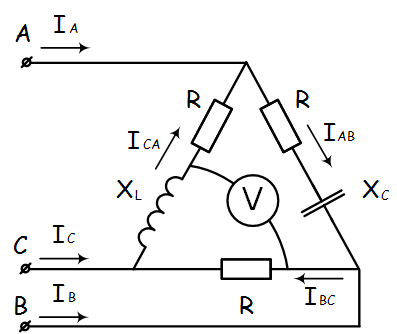



Как и в предыдущей задаче, в первую очередь определим комплексы сопротивлений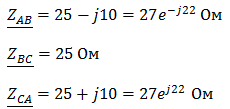

Фазное напряжение при данном соединении будет равно линейному, следовательно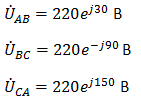

Фазные токи при несимметричной нагрузке не равны



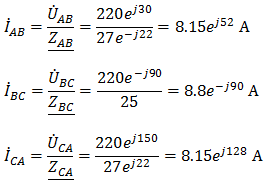Для определения линейных токов представим фазные токи в алгебраической форме комплексного числа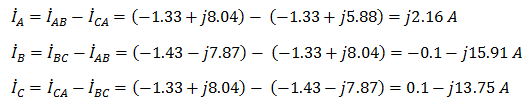



Сумма линейных токов



Равенство нулю суммы линейных токов является свойством любой трёхфазной системы.

Чтобы определить показания вольтметра, найдём сумму падений напряжения на x_L и R в соответствующих обмотках.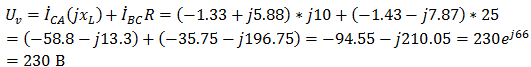



Задача№ 8Для заданного преподавателем трехфазного трансформатора из таблицы А.1 определить сопротивления обмоток R1, X1, R2, X2. Привести его схему замещения. Построить внешнюю характеристику и определить максимальный КПД трансформатора. Соединение обмоток трансформатора – Y/Δ («звезда/треугольник»), cosφ2 = 0,8.

Задача №9. По результатам опыта короткого замыкания ( 800 Рк = Вт, 20 U1к = В, I1к =100 А) определить параметры Rк и Хк схемы замещения трансформатора. Нарисовать Г-образную схему замещения трансформатора для данного режима.

Задача №10. Определить параметры Г-образной схемы замещения однофазного трансформатора номинальной мощностью 25 кВ·А по данным опытов холостого хода и короткого замыкания U1н = 220 В, U2н =127 В, 1х = ,I 41 А, P0 = 39 Вт, 8 1к = 8,U В при 80 , 1 = II Ркнк = Вт.

Задача №11. Определить КПД η и напряжение U2 на зажимах вторичной об16 мотки однофазного трансформатора при нагрузке, составляющей 50 % от номинальной и 8 0cos 2 ϕ = , , характер нагрузки индуктивный. Номинальные данные трансформатора следующие: 20000 Sн = кВ·А, 121 U1н = кВ, 2н = ,U 538 кВ, мощность холостого хода P0 = 47 кВт, мощность номинального короткого замыкания 129 Рк = кВт при напряжении 1к 050 U,U 1н ⋅= .

Задача №12. Трехфазный трансформатор имеет следующие номинальные данные: потребляемая мощность Sн = 20 кВ·А, высшее напряжение U1 = 6000 В, низшее напряжение 400 U2 = В, напряжение короткого замыкания U1к = 0,05 %, мощность холостого хода 180 P0 = Вт, мощность короткого замыкания Рк = 600 Вт, частота сети 50 f = Гц. Определить КПД при номинальной нагрузке и коэффициенте мощности 8

Переходные процессы в линейных электрических цепях
Задача №1

Решение: Определить независимые и зависимые   начальных условий для электрической цепи (см. рисунок 1.1).Независимые начальные условия  определяют по второму закону коммутации по схеме до коммутации (см. рисунок 1.2).

                                                                                          (1.8)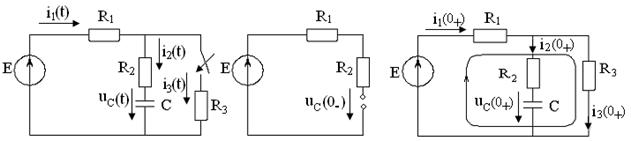

 



         Рисунок 1.1                                 Рисунок 1.2                    Рисунок 1.3

 

         Зависимые начальные условия находят для цепи после коммутации (см. рисунок 1.3), записав уравнения в соответствии с законами Кирхгофа: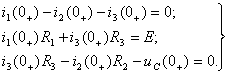

                               (1.9)

         Выразим из первого уравнения системы уравнений (1.9)   и подставим во второе уравнение. С учетом того, что  , получим: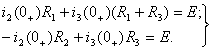

                                  (1.10)

         Решая систему уравнений (1.10), определим зависимые начальные условия  .

 

         Задача №2Длясхемы(см. рисунок 1.4) составить характеристическое уравнение и определить его корень: а) по однородному дифференциальному уравнению;

б) по методу входного сопротивления; в) определить корень по постоянной времени цепи  .



      Рисунок 1.4                      Рисунок 1.5                   Рисунок 1.6

 

Решение: а) Составим характеристическое уравнение по однородному дифференциальному уравнению. Запишем неоднородное дифференциальное уравнение относительно тока  :  ,

приравняем к нулю правую часть неоднородного уравнения, получим однородное дифференциальное уравнение:  .

         Заменим  на р,   на 1, получим характеристическое уравнение:

                                                    ,                                 (1.11)

отсюда корень характеристического уравнения

                                (1.12)

         б) Составление характеристического уравнения по методу входного сопротивления. Перейдём от заданной схемы цепи после коммутации к комплексной схеме (рис. 1.5) и запишем комплексное входное сопротивление

, заменим   на р , выражение   приравняем к нулю и получим характеристическое уравнение:

                                                  ,                                    (1.13)

корень которого вычисляется по формуле (1.12).

 

         в) Определить корни по постоянной времени цепи  .

Известно, что  . Для цепи с одним индуктивным элементом постоянная времени  . Эквивалентное сопротивление цепи  определяется относительно зажимов реактивного элемента (индуктивности), при этом

необходимо закоротить входной источник ЭДС (см. рисунок 1.6): .

 

1.2.2 Расчёт переходных процессов в цепях первого порядка.

Задача №3

Накопительная емкость импульсного модулятора передающего устройства РЛС (см. рисунок 1.7, а) после включения разряжается через разрядное сопротивление. Определить время, через которое напряжение на емкости уменьшится до уровня U=20 В, если U₀= 20 кВ, С= 5 мкФ, разрядное сопротивление R_p=10 кОм.

Решение: Конденсатор заряжен до напряжения  =U₀=20 кВ. Составим дифференциальное уравнение по второму закону Кирхгофа для цепи после коммутации (см. рисунок 1.7,б):

                           (1.14)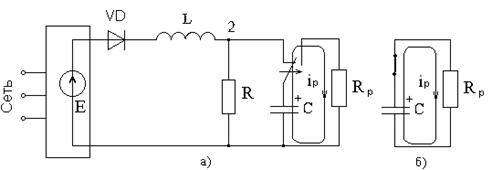

где 

 



        Рисунок 1.7

 

Решением дифференциального уравнения (1.14) является переходное напряжение на емкости, которое имеет вид

         Принуждённая составляющая напряжения   (для схемы после коммутации (см. рисунок 1.7,б) при  ) равна нулю:

         Свободная составляющая напряжения:

 B.

         И переходное напряжение будет равно: 

         Определим постоянную времени цепи  , используя соотношение

         Определим постоянную интегрирования Аиз начальных условий (при  ).

         Напряжение на ёмкости в переходном режиме будет равно:

                                                                             (1.15)

         Вычислим время разряда накопительной емкости до U=20 В из уравнений:

 или   отсюда 

         После логарифмирования получаем:

    

таким образом, время разряда накопительной емкости до U=20 В составляет примерно 7τ.

         График напряжения на емкости   построен в среде Mathcad  (см. рисунок 1.8).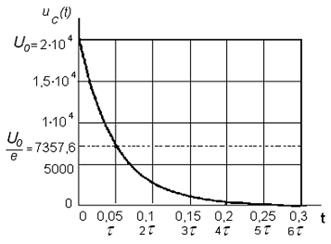



Рисунок 1.8

 

Вывод. Для регулирования длительности переходного процесса необходимо изменять в цепи постоянную времени  . Это достигается путем выбора параметров R и С. За время   свободная составляющая уменьшается в е = 2,718 раз.

Задача №4

 Интегрирующая цепь (см. рисунок 1.9) с параметрами R₁ = 30 Ом, R₂ = 20 Ом, С= 50 мкФ, Е= 100 В  подключается к сопротивлению R₂.

Определить закон изменения напряжения на конденсаторе и токов в ветвях в переходном режиме.

Решение: Определяют независимые начальные условия  . Из эквивалентной схемы для   (см. рисунок 1.10) находят 

Составляют систему дифференциальных уравнений по законам Кирхгофа для цепи после коммутации: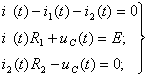

                                                                                         (1.16)

         Переходное напряжение  является решением ддифференциальных уравнений и представляется в виде: 



 Рисунок 1.9                    Рисунок 1.10                        Рисунок 1.11

 

         Определяют принуждённую составляющую напряжения   в установившемся режиме цепи после коммутации   из схемы (см. рисунок 1.11):

            

         Определяют свободную составляющую напряжения  .

         Постоянная времени цепи   находится по формуле:

            (1.17)

         Постоянную интегрирования определяют по начальному значению напряжения  :  , отсюда

.

         Записывают аналитические выражения для переходного напряжения

                    .                (1.18)

         Токи найдём по формулам:

    (1.19)

   

         Построение графиков напряжения и токов среде Mathcad (см. рисунок 1.12, 1.13).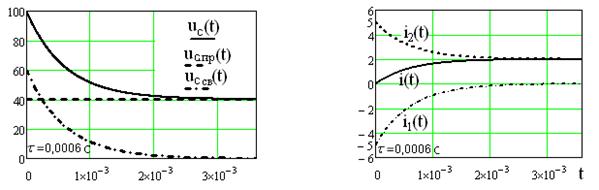

           



  Рисунок 1.12                                            Рисунок 1.13

 

Цепи  в виде резисторно-конденсаторного делителя нашли широкое применение в импульсных устройствах РЭТ.

 

1.2.3 Расчёт переходных процессов в цепях второго порядка.

 

Задача №5

 Параллельный колебательный контур (см. рисунок 1.14) подключается к источнику ЭДС Е= 125В. Определить закон изменения напряжения  для трех случаев: 1.R= 250 Ом, L= 667 мГн, С = 2 мкФ;

2. R = 100 Ом, L = 40мГн, С= 1 мкФ; 3. R = 100 Ом, L = 40мГн, С = 5мкФ.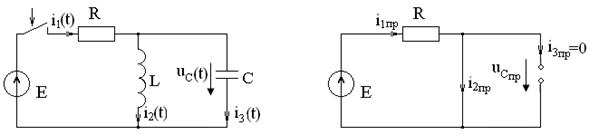

     Рисунок 1.14                                         Рисунок 1.15

 

Решение: Записывают независимые начальные условия    . Составляют систему дифференциальных уравнений по законам Кирхгофа для цепи после коммутации:

                                                                                       (1.20)

         Переходное напряжение   представляют в виде суммы принуждённой и свободной составляющих: 

         Определяют принуждённую составляющую напряжения на ёмкости. Так как в установившемся режиме цепи после коммутации (при  ) конденсатор шунтирован катушкой индуктивности накоротко (см. рисунок 1.15), принуждённая составляющую равна нулю: 

         Вычисляют свободную составляющую напряжения на ёмкости. Для этого составляют характеристическое уравнение, например, методом входного сопротивления и определяют его корни:

 или (после преобразований) 

откуда                                                                  (1.21.)

         Вид свободной составляющей напряжения зависит от типа корней характеристического уравнения. Для трех заданных значений параметров рассчитывают корни р_1,2.

1) R= 250 Ом, L= 667 мГн, С = 2 мкФ.

 

         Корни действительные и различные. Свободная составляющая напряжения на конденсаторе имеет вид: 

 

2) R = 100 Ом, L = 40мГн, С= 1 мкФ 

         Корни действительные и равные  , следовательно,

3)  R = 100 Ом, L = 40мГн, С = 5мкФ



         Корни комплексные сопряженные. Свободная составляющая напряжения на конденсаторе имеет вид: 

Постоянные интегрирования  и   определяют из начальных условий

. Из выражения    следует, что  , и задача сводится к определению  .Зависимое начальное условие   определяют из уравнений составленных по законам Кирхгофа (1.20), записанных для момента времени  :



и с учётом независимых начальных условий  , получим:

                                         (1.22)

Найдём u_c(t)для трех случаев корней:

1) R= 250 Ом, L= 667 мГн, С = 2 мкФ. Корни действительные и различные:   тогда:



При  : ,  , получим

отсюда А₁=250, А₂=-250,  и напряжение на ёмкости равно:                  

Графики напряжения u_c(t)и его составляющих выполнены в среде Mathcad (см. рисунок 1.16, а).

2) R = 100 Ом, L = 40мГн, С= 1 мкФ. Корни действительные и равные:  , тогда



при  : ,  , получим    , и напряжение на ёмкости равно: 

Графики напряжения u_c(t)и его составляющих выполнены в среде Mathcad (см. рисунок 1.16,б).

3) R = 100 Ом, L = 40мГн, С = 5мкФ. Корни комплексные сопряженные

 тогда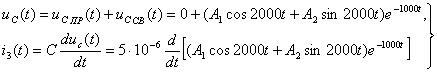



при  : ,  , получим    , отсюда   и напряжение на ёмкости будет равно: 

Графики напряжения u_c(t)и его составляющих выполнены в среде Mathcad (см. рисунок 1.16,в).