практика. Задача 1 Определить коэффициент полезного действия трехфазного трансформатора (%) со схемой соединения обмоток УУн, мощностью S
 Скачать 0.95 Mb. Скачать 0.95 Mb.
|
|
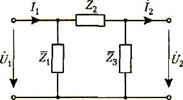
Четырёхполюсники и Однородная длинная линия Задача №1 Несимметричный четырехполюсник имеет параметры А = 1; В = 2,83еj45° Ом; С = j0,5 См; D = j1. Найти характеристические сопротивления четырехполюсника и постоянную передачи. Найдем характеристические сопротивления: 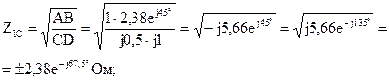 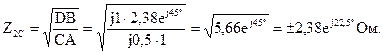 Отрицательные значения комплексного сопротивления не имеют физического смысла, так как они не реализуемы. Определим постоянную передачи: 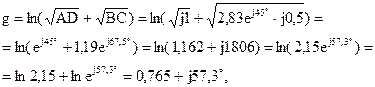 где коэффициент затухания , а коэффициент фазы или Задача №2 Для четырехполюсника, эквивалентная схема которого приведена на рис. 5.19, составить уравнения, выражающие зависимость комплексных напряжения входной ветви и тока выходной ветви от комплексных тока входной ветви и напряжения выходной ветви. Параметры элементов цепи: Z0=12 Ом, Z2=6 Ом, Z1=(4+j3) Ом. Искомую зависимость выражают уравнения четырехполюсника Н-типа: 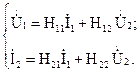 Коэффициенты Н11, Н12, Н21 и Н22 можно определить на основе рассмотрения исходной схемы сначала при разомкнутых первичных зажимах, а затем при короткозамкнутых вторичных полюсах с одновременным анализом уравнений Н-формы записи, соответствующим этим состояниям. При разомкнутых первичных зажимах = 0 и система уравнений примет вид: 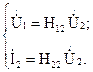 откуда запишем откуда запишем 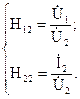 Для рассматриваемого режима: и тогда можно определить коэффициенты: 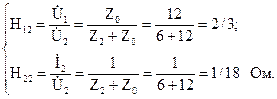 При короткозамкнутых вторичных полюсах =0 система уравнений примет вид: 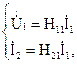 откуда запишем откуда запишем 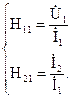 Для рассматриваемого режима: Тогда можно определить коэффициенты: 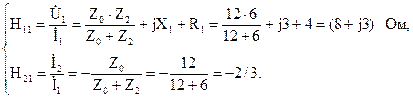 Задача №3 При питании четырехполюсника со стороны первичных зажимов были измерены U1, I1, P1 в двух режимах: а) холостого хода U1X = 100 B; I1X = 1 A; P1X = 0; б) в режиме короткого замыкания U1К = 100 B; I1К = 1,41 A; P1К = 100 Вт. В обоих случаях характер сопротивлений емкостный. При обратном включении четырехполюсника при закороченных первичных зажимах были измерены U2К = 100 B; I2К = 1 A; P2К = 100 Вт. Известно, что Z1K/Z2K = Z1X/Z2X. Рассчитать сопротивления прямого, обратного холостого хода и короткого замыкания. Определить по ним Z-параметры четырехполюсника. При прямом включении четырехполюсника входные сопротивления для режимов холостого хода и короткого замыкания по показаниям измерительных приборов определяются: где так как, согласно исходным данным, нагрузка носит чисто емкостный характер (Р1Х=0); где так как известно, что характер сопротивлений емкостный. где Сопротивление Z2K найдем из соотношения Z1K/Z2K = Z1X/Z2X: Уравнения четырехполюсника в Z-форме записи имеют вид: 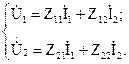 Для режима холостого хода при прямом = 0 и обратном = 0 включении четырехполюсника запишем: тогда тогда Для режима короткого замыкания на вторичных зажимах четырехполюсника ( ) запишем: 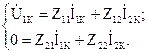 Выразим из второго уравнения ток на выходе четырехполюсника, и подставим полученное выражение в первое уравнение: Сопротивление короткого замыкания со стороны первичных зажимов: Отсюда рассчитаем коэффициенты: 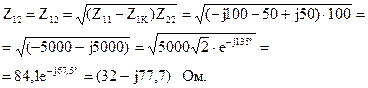 Задача №4 П 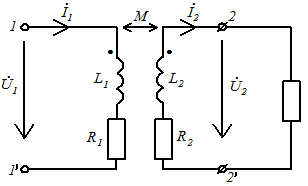 араметры линейного трансформатора (рис. 6.1): R1 = 2 Ом; L1 = 0,5 мГн; R2 = = 3 Ом; L2 = 0,72 мГн; k = 0,5; ƒ = 10 кГц; ω = 2πƒ = 62,8∙103. араметры линейного трансформатора (рис. 6.1): R1 = 2 Ом; L1 = 0,5 мГн; R2 = = 3 Ом; L2 = 0,72 мГн; k = 0,5; ƒ = 10 кГц; ω = 2πƒ = 62,8∙103.Определить: A, B, C, D. Рис. 6.1 Решение 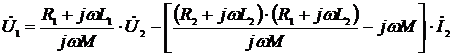 ; ;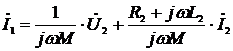 ; ;M = k∙ A = 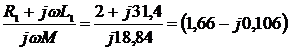 ; ;B = 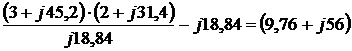 Ом; Ом;С = 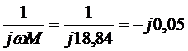 См; D = См; D = 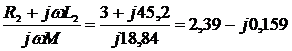 Задача №5 1) из основных уравнений четырехполюсников в режимах холостого хода и короткого замыкания; 2) по предварительно вычисленным сопротивлением холостого хода и короткого замыкания. Убедиться, что результаты удовлетворяют уравнению связи . Найти напряжение на разомкнутых вторичных зажимах при напряжении на первичных, равным 20В. Дано: ; при . Найти: A, B, C , D ,  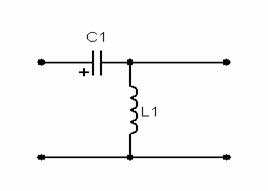 Рис.10.3 Решение: Запишем основные уравнения ; . В режиме холостого хода т.е. : ; . Для схемы рис.10.3 , , , В режиме короткого замыкания : ; . Для схемы рис.10.3 , следовательно , . При разомкнутых вторичных зажимах . Задача №6 Для четырехполюсников рис. 10.4 определить коэффициенты A, B, C , D и . Дано: , . Найти: A, B, C , D , Решение: В режиме холостого хода : ; , из схемы рис.10.3 ; , , , . . В режиме короткого замыкания : ; . Для схемы рис.10.4 , , 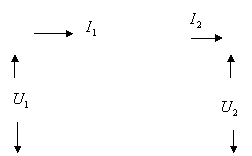 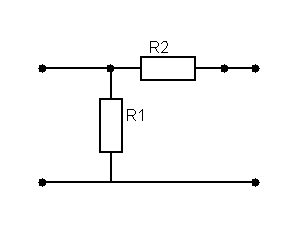 Рис.10.4 Задача №7 Сопротивления симметричного мостового четырехполюсника (рис. 10.5) равно , . Определить: 1) коэффициенты систем уравнении типа и типа ; 2) токи на входе и выходе, а так же напряжение на выходе при питании четырехполюсника от источника напряжения 100 мВ: а) при коротком замыкании; б) при холостом ходе на выходе.
Рис. 10.5 Дано: , . Найти: , , , Решение: 1. Уравнения типа : ; . При коротком замыкании т.е. ; где . При коротком замыкании схему рис. 10.5а можно изобразить так как показано на рис рис. 10.5б. Здесь и При холостом ходе : . Для симметричного четырехполюсника ; . С другой стороны (рис. 7.5а) , ; поэтому 2. Уравнения типа : ; . При холостом ходе : ; . С другой стороны (рис. 10.5а) , сопоставляя, находим , ; . А так же можно найти из соотношении , , , где . . .
Задача №8 «Рассчитайте распределение действующих значений напряжения и тока вдоль длинной линии без потерь (параметры L0=0,35 мкГн/м, C0=21 пФ/м). Частота передаваемого гармонического сигнала f=0,7 ГГц. Режим работы линии — Rн=2Zв. Мгновенное значение тока i2(t)=25sin(2πft+40o). Длина линии λ=18 см. Постройте графики U(y), I(y) и определите значение коэффициента бегущей волны». Дано L0=0,35 мкГн/м; C0=21 пФ/м; f=0,7 ГГц; Rн=2Zв; i2(t)=25sin(2πft+40o); λ=18 см. Решение Находим циклическую частоту: Найдем волновое сопротивление линии, предполагая, что сопротивление провода нулевое, а сопротивление между проводами бесконечно («линия без потерь»). 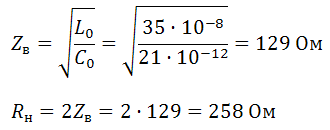 Находим постоянную распространения: Тогда коэффициент фазы равен: Введем условное обозначение m: 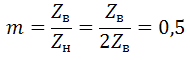 Распределение тока в линии в зависимости от расстояния от конца линии: 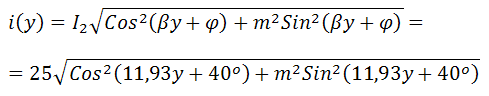 Мгновенные значения напряжения: Распределение напряжения в линии в зависимости от расстояния от конца линии: 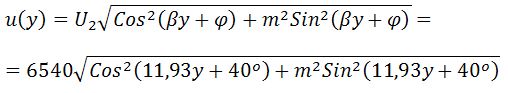 График напряжения на линии, как функции от расстояния от конца линии y: 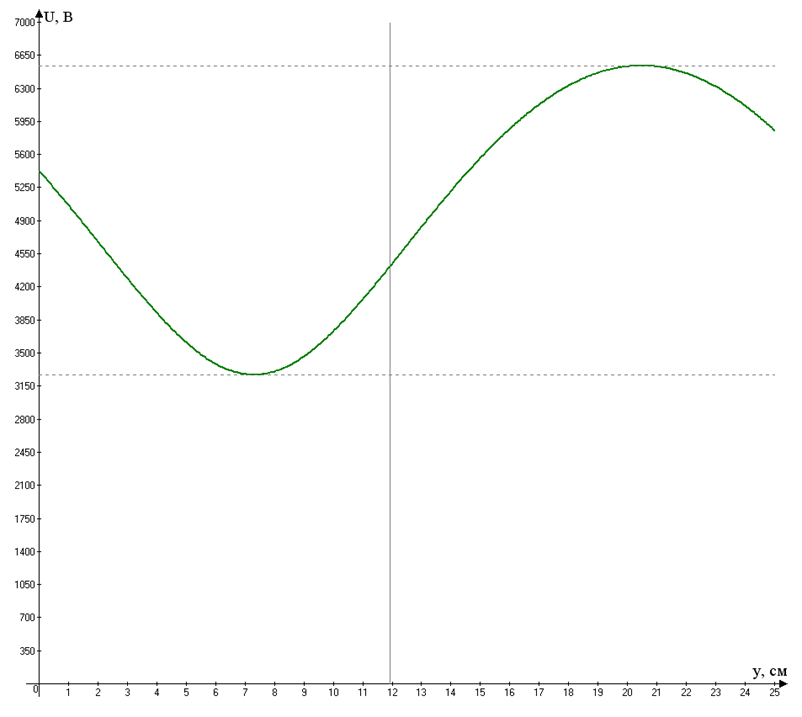 График построен дальше начала линии (обозначено вертикальной линией) для определения минимума и максимума напряжения смешанной волны. Коэффициент бегущей волны – отношение минимума напряжения смешанной волны к её максимуму – определяем по графику. Kб.в.=3270/6540=0,5; График тока на линии, как функции от расстояния от конца линии y: 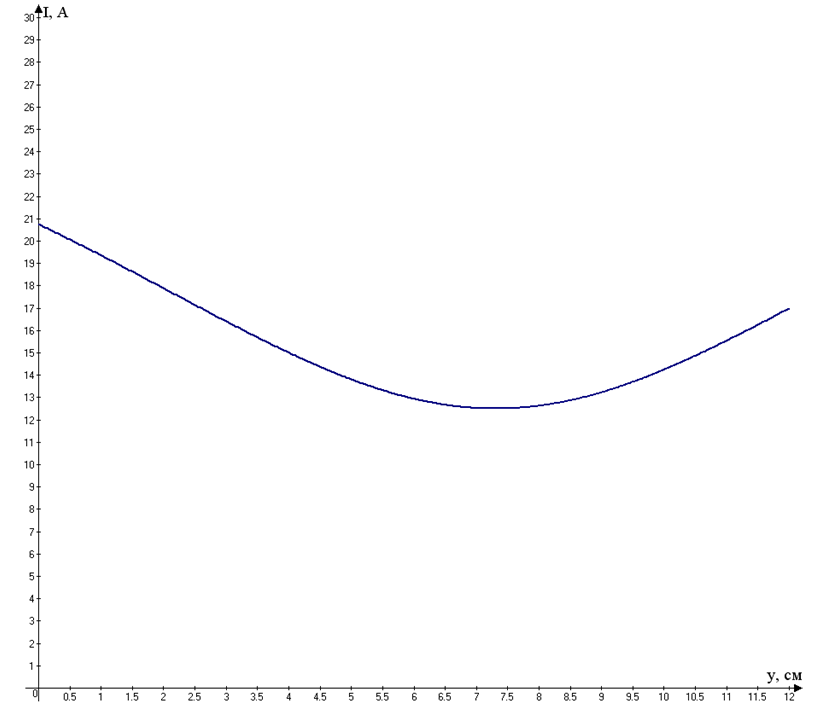 |