Математика древнего Вавилона. реферат. Реферат аспиранта 1 г о. кафедры Механики композитов Какушева Эльдара Рамазановича научный
 Скачать 2.02 Mb.
|
 Московский Государственный Университет им. М. В. Ломоносова. Механико-математический факультет. Математика Древнего Вавилона. реферат аспиранта 1 г. о. кафедры Механики композитов Какушева Эльдара Рамазановича научный руководитель Шешенин С. В. руководитель семинаров по философии Перминов В. Я. Москва 2010 1. Древнее Двуречье. Вавилонская цивилизация ведет свои корни от 4000 г. до н.э., от шумеров из Месопотамии. Известно о них, однако, не много. Шумер был впервые основан между 4500 и 4000 гг. до н.э. несемитским народом, который не говорил на шумерском языке. Эти люди теперь называются убейдиане в честь деревни Аль-Убейд, где были впервые обнаружены их останки. Об их математике известно еще меньше. Из того малого, что известно, шумеры Месопотамской долины строили дома и храмы и украшали их художественной керамикой и мозаиками в геометрических узорах. Убейдиане были первой цивилизирующей силой в регионе. Они осушали болота для сельского хозяйства, развивали торговлю и основали такие отрасли промышленности, как ткачество, обработку кож, обработку металлов, строительство с помощью каменной кладки и изготовление глиняной посуды. Народ, называвшийся шумерами, чей язык преобладал на этой территории, вероятно, происходил из местности неподалеку от Анатолии и, вероятно, появился в Шумере около 3300 г. до н.э. Ранние шумеры имели знаки для чисел, как показано ниже. Вследствие дефицита ресурсов, шумеры использовали глину, которой было очень много. Их письмо подразумевало использование стилоса для вырезания на мягкой глиняной табличке. Это предшествовало 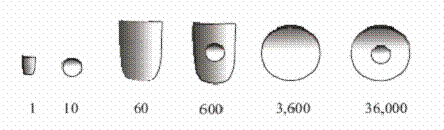 клинописи, которую шумеры развивали в течение четвертого тысячелетия. Она, вероятно, предшествует египетскому иероглифическому письму и, возможно, была самой ранней формой письменной коммуникации. Вавилоняне и другие культуры, включая ассирийцев и хеттов, унаследовали шумерские законы и литературу и, что важно, их стиль письма. Здесь мы сосредотачиваемся на более позднем периоде месопотамской цивилизации, который поглотил шумерскую цивилизацию. Месопотамские цивилизации часто называются вавилонянскими, хотя это и не совсем правильно. На самом деле, Вавилон не был первым большим городом, хотя вавилонской называется вся цивилизация. Вавилон, даже во времена своего существования, не всегда был центром месопотамской культуры. Этот регион, по крайней мере, та его часть, которая находится между двумя реками, Тигром и Евфратом, также называется Халдеей. Время существования Месопотамской цивилизации начинается с 2000-600 гг. до н. э. Несколько ранее мы видим объединение местных принципатов сильными лидерами – что-то похожее происходило и в Китае. Одним из самых сильных был Саргон Великий (приблизительно 2276-2221 гг. до н.э). Под его правлением регион был объединен в империю, названную династией Аккада, а аккадский язык начал замещать шумерский. Примерно в это время были проведены обширные общественные работы, такие как строительство оросительных каналов и укреплений в виде насыпей. Они были необходимы вследствие географического положения и необходимости кормить большое население. Для процветающей цивилизации такие сооружения были необходимы, так как Тигр и Евфрат разливались при сильных дождях, а глинистая почва могла поглотить не слишком много влаги.
Вавилонские «тексты» доходят до нас в виде глиняных табличек, обычно примерно размера ладони. Они написаны клинописью, клинообразным алфавитом, имевшим такую форму благодаря стилосу, который использовался для письма. Обычно находят два типа математических табличек: тексты-таблицы и тексты-задачи. Тексты-таблицы собственно являются таблицами величин для каких-то целей, например, таблицы умножения, таблицы весов и мер, таблицы обратных величин и подобные им. Многие из текстов-таблиц, очевидно, являются учебными табличками, написанными писцами-учениками. Второй класс табличек посвящен решениям или методам решения алгебраических или геометрических задач. Некоторые таблички содержат до двухсот задач постепенно увеличивающейся сложности. Без сомнения, роль преподавателя была весьма значительной. Время великой империи подошло к концу. Однако приблизительно в 300 г. до н.э. начался новый период вавилонской математической истории, когда к власти пришли Селевкиды, преемники Александра Великого. Этот 300-летнтй период принес большое количество астрономических записей, которые являются примечательно математическими – сопоставимыми с Альмагестом Птолемея. Однако математические тексты редки для этого периода. Это указывает на актуальность и долговечность математических текстов старовавилонского периода (приблизительно с 1800 до 1600 до н.э.), и мы сосредоточим свое внимание именно на этом периоде. Использование клинописи сформировало крепкие связи. Законы, налоговые счета, истории, школьные уроки, личные письма выдавливались на мягких глиняных табличках и затем высушивались на горячем солнце или в духовках. В одном регионе, где располагался древний Ниппур, были восстановлены около 50 000 табличек. Многие университетские библиотеки имеют обширные коллекции клинописных табличек. Самые большие собрания из Ниппурских раскопок могут быть найдены, например, в Филадельфии, Йене и Стамбуле. Всего до сих пор было восстановлено как минимум 500 000 табличек. И даже несмотря на это, считается, что большая часть существующих табличек все еще погребена под руинами древних городов. Расшифровка клинописи проходила аналогично тому, как это происходило с египетским иероглифическим письмом. Действительно, так же, как и в случае иероглифов, ключом к расшифровке стала трёхъязычная надпись, найденная членом Британского офиса, Генри Роулинсоном (1810-1895), бывшим советником Шаха. В 516 г. до н.э. Дарий Великий, правивший в 522-486 гг. до н.э., повелел выгравировать долговечный монумент в честь своего правления в виде барельефа на 100х150-футовой поверхности на каменном утесе, «Горе Богов» в Бехистуне у подножия Загроса в области Керманшаха современного Ирана по дороге между современным Хамаданом (Иран) и Багдадом, около города Бизотун. В старину название деревни было Багастана, что означает «место, где живут боги». Как и Розеттский камень, надпись была сделана на трех языках: старом персидском, эламитском и аккадском (вавилонском). Однако все три языка были тогда неизвестны. Расшифровка стала возможна только потому, что старый персидский язык имеет всего 43 символа и серьезно изучался с начала девятнадцатого века. Продвижение было очень медленным. Роулинсон смог правильно расшифровать 246 символов и, более того, он обнаружил, что один и тот же символ может означать различные согласные звуки в зависимости от гласного, который за ним следовал (полифония). Значительные публикации на эту тему появились только в 20-ом веке. 2. Источники.
В древнем Двуречье общественными работами руководили писцы, занимавшиеся также учетом хозяйства, составлением торговых документов и деловой перепиской. Математические клинописные тексты носят учебный характер и содержат в основном расчетные задачи. 3. Вавилонские числа. В Вавилоне мы впервые встречаемся с последовательной позиционной нумерацией. Эта нумерация была построена на использовании только двух клинописных знаков  и  , при записи чисел от 1 до 59, а при записи чисел от 60 и т.д. использовался еще знак  . Они имели клинообразный вид, так как вавилоняне писали н глиняных дощечках палочками треугольной формы. обозначал 1 и 60, обозначал 10 и 600. При записи чисел от 1 до 59 знаки единицы и десятки записывались столько раз, сколько в данном числе единиц и десятков, причем разряды располагались в том же порядке, что и у нас. Числа кратные 60, от 60 до 59*60 точно так же, как соответственные множители от 1 до 59 слева от чисел, меньших 60. При отсутствии разряда применялся знак . В Вавилонской нумерации число 60 играет такую же роль как в нашей 10, поэтому эту нумерацию называют шестидесятеричной. Приведем примеры:
Впоследствии знак стал обозначать не только 1 и 60, но и 3600, и любые числа  , а также  и любые другие числа вида  . Знак стал обозначать не только 10 и 600, но и 36000 и любые числа вида  , а также  и любые числа вида  . Таким образом вавилоняне кроме шестидесятеричной системы счисления пользовались шестидесятеричными дробями.В более позднее время вавилоняне ввели знак  , имеющий значение нуля, и если m-n>1, между числами, кратными  и , вставлялось m-n-1 таких знаков.Вавилоняне обладали также специальными знаками для дробей  ,  и  .Нет ясной причины, почему вавилоняне выбрали шестидесятеричную систему. Согласно Феону Александрийскому, комментатору четвертого века нашей эры, выбор, возможно, был сделан в интересах метрологии: число 60 делится на числа 2,3,5,10,12,15,20, и 30. «Наследство» этой системы все еще существует сегодня в единицах измерении времени и углов. Тем не менее, был предложен целый ряд теории для объяснения выбора вавилонянами основы 60. Число дней в году – 360 – было причиной разделения круга на 360 градусов, а то, что длина хорды, составляющей одну шестую длину окружности, равна радиусу, было причиной естественному разделению круга на шесть равных частей. Это, в свою очередь, сделало 60 естественной единицей счета (Мориц Кантор, 1880). Вавилоняне делили день на 12 часов, а час – на 60 минут. Таким образом, две наши минуты равны одной минуте вавилонян (Леман-Хопт, 1889). Более того, (месопотамский) Зодиак был разделен на двенадцать равных секторов по 30 градусов каждый. Основа 60 обеспечила удобный способ выражения дробей из различных систем, которые могут быть необходимы для преобразования весов и мер. В египетской системе были значения 1/1, 1/2, 2/3, 1, 2..., 10. Объединяя их, мы видим, что для знаменателей этих дробей необходим множитель 6. Он, вместе с основой 10, дает 60 как основу для новой системы (Нейбауэр, 1927). Число 60 есть произведение числа планет (в то время было известно 5 планет) на число месяцев в году, 12 (Д. Дж. Бурстин, 1986). Комбинация двенадцатеричной системы (с основой 12) и системы с основой 10 естественным образом приводит к системе с основой 60. Более того, мы используем «наследство» двенадцатеричной системы и сегодня, когда считаем некоторые предметы потребления, например яйца, дюжинами. В английской системе мер жидкостей встречаются многочисленные примеры двенадцатеричных величин. Как видно из таблицы ниже, градации с основой 12 (основой 3 или 6?) и основой 2 смешаны. Аналогичные величины существуют и в древних римской, шумерской и ассирийской системе измерений.
Заметьте, что в первой колонке таблицы жидких/сухих мер отсутствует важная кулинарная мера – 1/4 чашки, которая равна 12 чайным ложкам. Все объяснения, приводимые выше, имеют ту общую черту, что пытаются представить правдоподобные аргументы, основанные на каком-либо специфическом аспекте их общества. Видя, как развиваются различные системы сегодня, мы неизбежно приходим к догадке, что здесь может работать чья-то сильная воля. Создание или навязывание системы счисления и применение ее во всей цивилизации должно было быть деянием политической системы огромной мощи и централизованности (Стоит только вспомнить неудачную попытку Америки перейти на метрическую систему начиная с 1971). Решение об адаптации основы системы счисления должно было быть принято правителем по причинам более серьезным, чем советы купцов или генералов, по какой-либо насущной необходимости. Или, возможно, в связи с консолидацией власти в Шумерии, где могли конкурировать несколько систем счисления. Возможно, основа 60 была выбрана как компромиссный вариант. В 1854 г. в Сенкерахе на Евфрате были найдены две таблички, датируемые 2000 г. до н.э. В них даются квадраты чисел до 59 и кубы числе до 32. Вавилоняне использовали формулу  для упрощения умножения. Деление основывалось на умножения, а именно:  Вероятно, вавилоняне не использовали деление на бумаге «в столбик». Вавилоняне знали некоторые приближения нерегулярных дробей:  Однако они, видимо, не заметили, что эти дроби имеют бесконечные периодические продолжения. Вероятно, они также имели элементарное преставление о логарифмах. Точнее говоря, известны тексты, где рассматривается вопрос нахождения экспоненты для заданных чисел. |
