Математика древнего Вавилона. реферат. Реферат аспиранта 1 г о. кафедры Механики композитов Какушева Эльдара Рамазановича научный
 Скачать 2.02 Mb.
|
|
6. Геометрия у вавилонян.
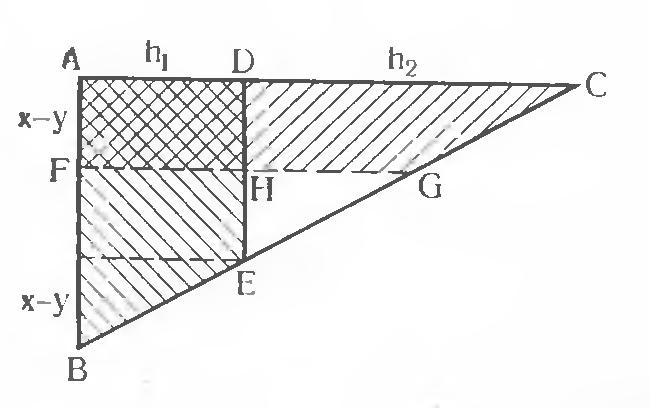
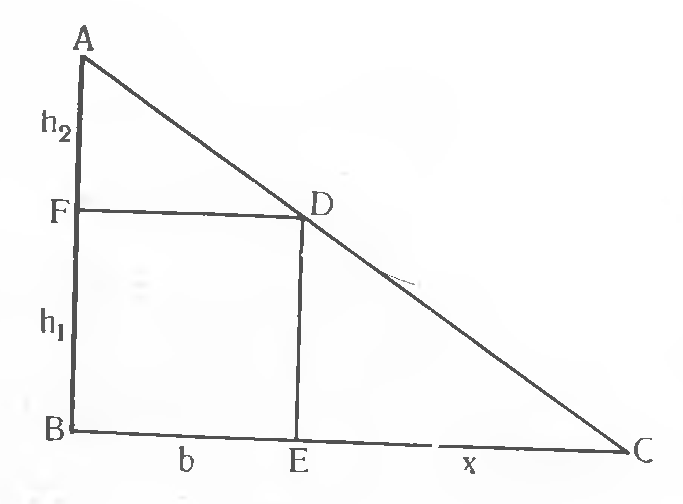
 =3 определяли площадь круга. Однако вавилоняне были близки к совершенствованию значения . Например, одна из табличек, найденной в 1936 г. в Сузах, содержит следующее приближение  Это дает эффективную оценку  (неплохо).Вавилоняне знали, что высота равнобедренного треугольника делит основание пополам, угол, вписанный в полуокружность, является прямым (Фалес). Теорема Пифагора.  В клинописных текстах впервые появляется, и притом для общего случая, теорема Пифагора. Как пришли Вавилоняне к теореме неизвестно. Быть может, они сначала заметили, что некоторые треугольники с целочисленными сторонами a, b, c, удовлетворяющими равенству  , а потом распространили такое свойство на все прямоугольные треугольники. Во всяком случае, еще в древневавилонскую эпоху знали множество троек «пифагоровых чисел». До нас дошла одна таблица, содержащая 15 строчек чисел вида  , b и c.Теорема Пифагора находила в Вавилоне разнообразные применения. С ее помощью вычисляли, например, диагональ квадрата и радиус окружности, описанной вокруг равнобедренного треугольника, по боковой стороне b и основанию 2a. Сохранился, хотя и не полностью, древневавилонский чертеж, на котором видны аккуратно проведенная циркулем дуга описанной окружности и числовое значение радиуса. Также в древневавилонских текстах имеется такая задача: даны высота стены и равная длина шеста, а также отрезок на который отступает его верхний конец; требуется найти на сколько отступит нижний конец от стены. Наконец, теорема Пифагора несомненно была использована вавилонскими учеными, когда они рассматривали правильные многоугольники. Правильные многоугольники. Строгая теория правильных многоугольников явилась одним из выдающихся достижений пифагорейской школы. В некоторых клинописных текстах были обнаружены таблицы констант, которыми пользовались в хозяйственных расчетах. Эти таблицы содержали константы  ,  ,  , причем они соотнесены с правильными пяти-, шести- и семиугольниками соответственно. Они дают площади названных многоугольников, если сторона принята за единицу.Подобие и пропорциональность. Некоторые задачи, которые мы бы решали, используя подобие треугольников, вавилоняне решали, видимо, по – иному. Такова, например, следующая задача. В прямоугольном треугольнике ABC даны катет  и площадь S трапеции ABED, отсекаемая отрезком DE=y, перпендикулярным катету AC. Нужно найти x и y. Эту задачу легко решить пользуясь признаками подобия треугольников. Но здесь не обязательно прибегать к подобию. Если произвести сдвиг треугольника DEC в положение FBG, то можно заметить, что площади
 Вполне возможно, что именно так поступали древневавилонские математики. Конечно, это предполагает, по существу, знакомство с некоторыми свойствами параллельных прямых ( . Спрашивается, на сколько (x) следует
 проще всего следует из подобия прямоугольных треугольников AFD и DEC.Многие другие задачи также говорят в пользу предположения, что подобием прямоугольных треугольников пользовались. 7. Значение математики древнего Вавилона. Насколько мы можем судить по известным до сих пор текстам, математика в древнем Вавилоне достигла более высокого уровня, чем в древнем Египте, хотя и она была далека от того идеала дедуктивной науки, который сформировался в Греции и классическим образом которого стали «Начала» Евклида. Несмотря на гораздо больший объем фактических знаний, более совершенные приемы вычислений, возникновение целых новых направлений и очевидный рост элементов логической дедукции, в древневавилонской математике внутренние логические связи между многочисленными правилами были еще слабыми и отдельные цепочки выводов не объединялись в целостные системы. Древние математики Двуречья, блестяще решавшие задачу приближенного вычисления чисел, обратных неправильным, или значений встречавшихся им в геометрии квадратных корней из неквадратных чисел, прошли мимо открытия периодических шестидесятиричных дробей и иррациональных чисел. При всем этом открытия, сделанные вавилонскими писцами, поражают своим размахом. Здесь впервые возникла система счисления, основанная на позиционном принципе и, позднее, на употреблении знака нуля. Здесь впервые же была разработана алгебра линейных и квадратных уравнений и даже рассмотрены простейшие уравнения более высоких степеней. Если к этому добавить открытие теоремы Пифагора и начала учения о правильных многоугольниках в области геометрии и в самой тесной связи с задачами геометрии постановку и решение первых задач теории чисел, то значимость достижений математики древнего Вавилона не может вызывать сомнений. Влияние вавилонской шестидесятеричной нумерации отразилась на арифметике дробей и делении круга, которым пользуются до сих пор. Список литературы. История математики с древнейших времен до начала нового времени под ред. А. П. Юшкевича. М.: Наука, 1970 г. Б. Л. ван дер Варден. Пробуждающаяся наука: Математика древнего Египта, Вавилона и Греции. Пер. И. Н. Веселовского. М.: Государственное издательство физико-технической литературы, 1959 г. Дж. Дональд Ален. Вавилонская математика. Перевод: Воронина А.Н. http://kosilova.textdriven.com/narod/studia3/math/translatio/babylon.htm |
