Математика древнего Вавилона. реферат. Реферат аспиранта 1 г о. кафедры Механики композитов Какушева Эльдара Рамазановича научный
 Скачать 2.02 Mb.
|
|
4. Вычислительная техника. Позиционный характер вавилонской нумерации и довольно большое ее основание, естественно, наложили печать на всю технику вычислений. В дальнейшем мы будем отделять целую часть числа, записанного в шестидесятеричной системе, точкой с запятой, а отдельные разряды – запятой. Например:  .Сложение и вычитание производили так же, как это делается в десятичной позиционной системе целых и дробей. При умножении затруднение, связанное с большим основанием системы нумерации, преодолевалось с помощью специальных таблиц. Вавилоняне пользовались не одной таблицей умножения 59*59, запомнить которую не легко, так как она содержит 1770 элементов(в нашей десятичной таблице их всего 45). Для умножения, как и для деления, существовал обширный набор таблиц. Прежде всего, имелись таблицы произведения чисел n, называемых теперь «заглавными», на числа m=1, 2, 3…, 19, 20,30, 40, 50. Операцию деления в вавилонской математике можно назвать проблемой №1. нынешний школьный процесс поразрядного деления не был полностью известен в те далекие времена. Вавилоняне деление a на b свели к умножению c = ad, и даже термина «делить» у них не существовало. Они брали обратную часть от b, это было d, умножали a на d, получали c. Главное внимание, таким образом, было уделено составлению таблиц обратных величин. Приведем примеры таких таблиц:
Широкое применение различных таблиц – характерная особенность математики древнего Вавилона. 5. Арифметические задачи. Представления об арифметической и геометрической прогрессиях у древних вавилонян были хорошо развиты. Они знали правило суммирования n членов арифметической прогрессии с данными первым и последним членами:   .В текстах древних вавилонян находятся задачи с суммированием n членов геометрической прогрессии, например 1, 2,  , …,  , правда, способ решения не совсем ясен. По - видимому, было обнаружено, что в такой прогрессии  .В клинописных текстах были найдены первые задачи на проценты. Древний Вавилон стоял на перепутье торговых караванов многих народов, поэтому рано появились денежные знаки и кредит. Начисляли здесь 12 на 60, т.е., по – нашему, 20%. Вычислялись также сложные «проценты». Особый интерес представляет применение, которое получили арифметические прогрессии в астрономии. Среди таблиц 3-2 вв. до н.э. находится таблица лунных эфемерид для 179 г., в которой первый столбец – номер месяца, второй – число и шестидесятеричные дроби суток для момента соединения Луны с Солнцем:
Первые три числа второго столбца – возрастающая арифметическая прогрессия с разностью  , следующие шесть чисел составляют убывающую прогрессию с той же разностью и, наконец, последние четыре числа этого столбца снова образуют возрастающую прогрессию с той же разностью. Наблюдаемые величины времен соединений Луны и Солнца подчиняются значительно более сложной периодической закономерности, но вавилонские астрономы не могли ее точно получить и упрощали результаты наблюдений таким образом, чтобы они выражались уже известными им схемами.6. Алгебра у вавилонян. В греческой математике существует четкая граница между алгеброй и геометрией. Везде, где это возможно, греки использовали геометрический подход. Только в более поздних работах Диофанта большое значение придается алгебраическим методам. С другой стороны, вавилоняне столь же определенно придерживались «алгебраической» точки зрения. Они допускали операции, которые
Во-первых, математические выражения были сугубо риторическими; до прихода символизма в работах Диофанта было еще два тысячелетия, а после него символизм приобрел важное значение лишь в 16-ом веке в работах Виета. Например, обозначением неизвестного была длина. Обозначением квадрата неизвестного была площадь. При решении двумерных линейных систем неизвестные обозначались длина и ширина, а при решении трехмерных систем – длина, ширина и глубина. Уравнения первой степени. Уравнения первой степени и их системы в клинописных текстах встречаются редко. Способы решения применялись различные: исключение неизвестных, введение вспомогательных неизвестных и др. Пример из текстов древневавилонского периода: 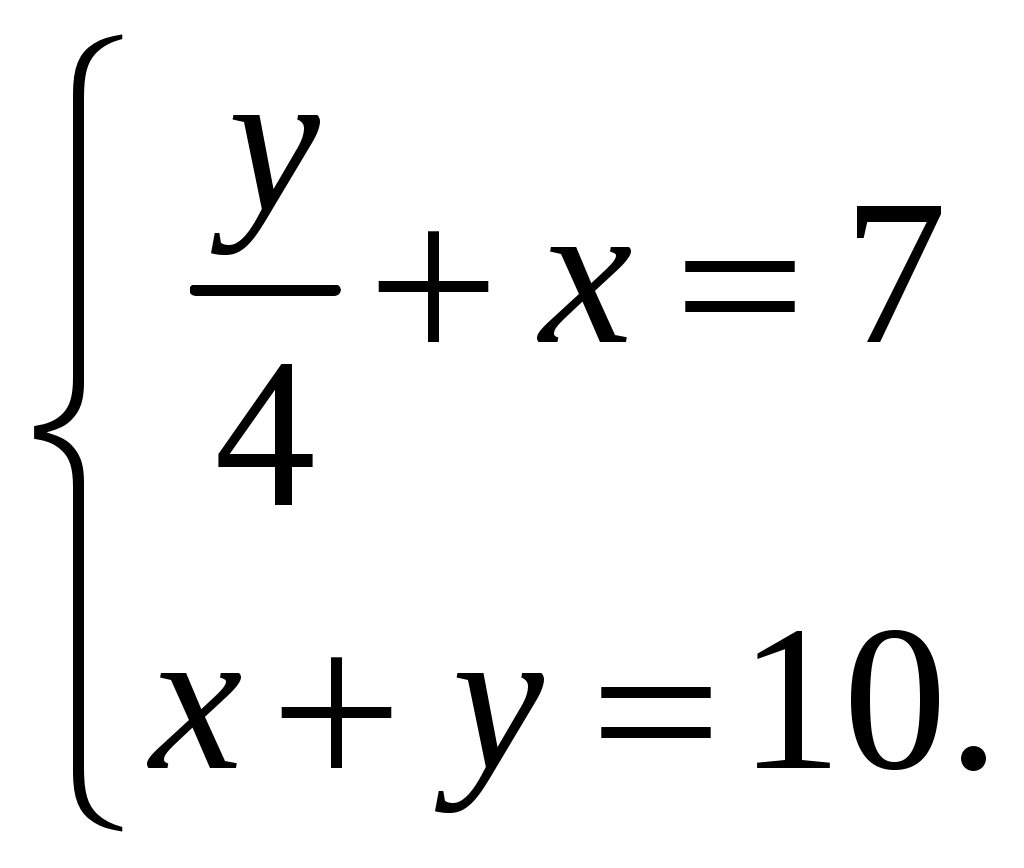 Судя по вычислениям в тексте, древний вычислитель после освобождения от дробного коэффициента в первом уравнении и вычитания из него второго получил 3x=18, x=6 и y=4. Для решения линейных систем применялся, например, поразительно искусный метод, при котором задача с двумя переменными сводилась к задаче с одной с помощью процесса «устранения», немного напоминающего гауссово устранение. Задача: решите 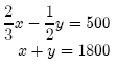 Решение. Выберем  такие, что Таким образом,  . Теперь применим модель Мы получим 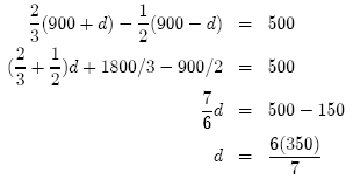 Таким образом,  и, следовательно, Квадратные уравнения. Вавилоняне не знали ни отрицательных чисел, ни тем более комплексных, и уравнения вида  (a>0, b>0, c>0), не имеющие положительных корней, безусловно не рассматривали. Позднее ученые средних веков различали три канонические формы трехчленных квадратных уравнений, которые могут иметь положительные корни:  (1) (2) (3)или  (1’) (2’) . (3’)В клинописных текстах квадратные уравнения принадлежат форм (1) и (2), которые записывали в виде  или  .Форма (3) или, что то же, (3’), в них не встречается, но имеются задачи, выражающиеся канонической системой  Уравнения (1) и (2) всегда имеют один положительный корень (другой – отрицательный), и, с точки зрения древнего математика, это положение было самым естественным. Поскольку лишь форма (3) или (3’) может иметь два положительных корня, а она в текстах не обнаружена, преждевременно ставить вопрос, известно ли было вавилонянам, что в этом случае корень может иметь два различных значения. Рассмотрим пример решения уравнения:  В тексте сказано: «Я вычел из площади сторону моего квадрата, это 14,30». Далее идет вычисление: «Ты берешь 1, коэффициент. Ты делишь пополам 1, это 0;30. Ты умножаешь 0;30 на 0;30, это 0;15. Ты складываешь это с 14,30 и это есть 4,30;15, что является квадратом для 29;30. Ты складываешь 0;30, которое ты умножал, с 29;30, получается 30, сторона квадрата». Как видно вычисление полностью соответствует нашей формуле 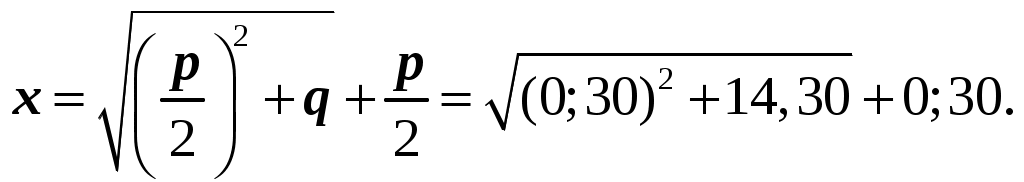 Учение о квадратных уравнениях явилось основой существенно нового этапа в развитии математики, когда наряду с арифметикой и измерением фигур ее полноправной частью стала алгебра. Для решения квадратных уравнений понадобилось многое, и сами они вызвали к жизни цепь новых понятий. В целом математическое мышление поднялось на новый, значительно более высокий уровень общности и отвлеченности и приобрело большую силу. Уравнения высоких степеней. Вавилоняне решали также некоторые задачи, выражающиеся кубическими уравнениями. Ставился вопрос об определении ребер прямоугольного параллелепипеда по данной сумме объема и площади одной грани, и некоторым условиям, наложенным на ребра. В зависимости от этих условий получаются уравнения первой, второй и третей степеней. 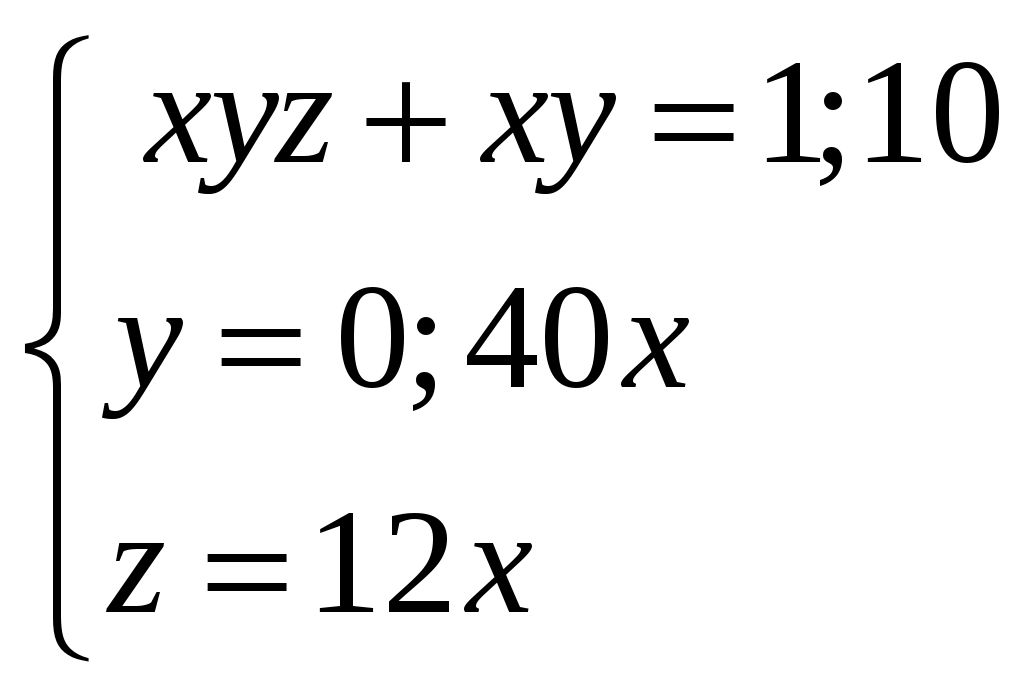 Задача приводится к уравнению  .В текстах обнаружено даже уравнение восьмой степени, которое, впрочем, является квадратным относительно  и приводится к виду  .Приближенное вычисление корней. В задачах на квадратные и высшие уравнения корни всегда являются рациональными. Однако в геометрических приложениях вавилоняне встречались и с проблемой извлечения квадратных корней из неквадратных чисел. Тексты ничего не сообщают о том, приблизились ли математики древнего Двуречья к идее иррационального числа. Они содержат неоднократно встречающееся затем и у других народов правило  с объяснением, основанным на том, что  ,а  мало и им можно пренебречь.Для вычисления квадратного корня также использовался метод среднего. Метод среднего.
 . Формально говоря, мы имеем следующий алгоритм:1. Возьмем  как начальное приближение.2. Идея: Если  , то  .3. Поэтому возьмем 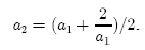 4. Повторим процесс. Пример. Возьмем 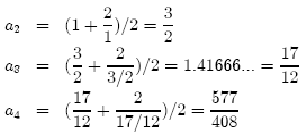 . Тогда мы имеем Если теперь выполнить этот процесс в шестидесятеричной системе, начиная с  , используя вавилонскую арифметику без округлений, то получится значение 1; 24,51,10.Замечание:  обычно использовалось как краткое, грубое, зато готовое приближение. При использовании шестидесятеричной системы счисления одним символом можно записать достаточно много информации. |
