Реферат функции
 Скачать 64.38 Kb. Скачать 64.38 Kb.
|
|
РЕФЕРАТ Функции Понятие функции – одно из важнейших понятий математики. Пусть даны два множества Х и У и каждому элементу х Х поставлен в соответствие единственный элемент у У, который обозначен через f(х). В этом случае говорят, что на множестве Х задана функция f и пишут: f : Х У. Например, пусть Х = а; b; с; d, У = ; ; ; и функция f:Х У определена так: f(a) = , f(b) = , f(c) = f(d) = . Наглядно эту функцию можно представить следующим образом: множества Х и У изобразим в виде областей, элементы множеств – в виде точек, а установленное соответствие – в виде стрелок:  Идея функциональной зависимости зародилась в античной математике, но она еще не была явно выражена и не являлась самостоятельным объектом исследования, хотя и был известен широкий круг конкретных систематически изучавшихся функциональных соответствий. В зачаточной форме понятие функции появляется в трудах ученых в средние века, но лишь в работах математиков 17 века, и прежде всего П. Ферма, Р. Декарта, И. Ньютона и Г. Лейбница, это понятие стало оформляться как самостоятельное. Термин «функция» впервые появился у Г. Лейбница. Для задания функции использовались геометрические, аналитические и кинематические концепции, но постепенно стало превалировать представление о функции как о некотором аналитическом выражении. В четкой форме это было сформулировано в 18 веке. И. Бернулли принадлежит определение, что «функцией переменной величины… называется количество, составленное каким угодно способом из этой переменной величины и постоянных». Л. Эйлер, приняв это определение, заменил в нем слово «количество» словами «аналитическое выражение». Несколько позже у Л. Эйлера появился уже и более общий подход к понятию функции как зависимости одной переменной величины от другой. Эта точка зрения получила свое дальнейшее развитие в трудах Ж. Фурье, Н.И. Лобачевского, П. Дирихле, Б. Больцано, О. Коши, где стало выкристаллизовываться представление о функции как о соответствии между двумя числовыми множествами. Так, в 1834 году Н.И. Лобачевский писал: «Общее понятие функции требует, чтобы функцией от х называть число, которое дается для каждого х и вместе с х постепенно изменяется. Значение функции может быть дано или аналитическим выражением, или условием, которое подает средство испытывать все числа и выбрать одно из них; или, наконец, зависимость может существовать и оставаться неизвестной». Определение функции как соответствия между двумя произвольными (не обязательно числовыми) множествами в 1887 году было сформулировано Р. Дедекиндом. Понятие соответствия, а следовательно, и понятие функции иногда сводится к другим понятиям (множеству, отношению или другим теоретико-множественным и логико-математическим концепциям), а иногда принимается за первичное, неопределяемое понятие, поскольку, как это выразил, например, А. Черч: «В конечном счете понятие функции – или какое-либо сходное понятие, например, понятие класса, - приходится считать первоначальным, или неопределимым». Ниже рассматривается понятие функции, основанное на понятии множества и простейших операций над множествами. Пусть даны два множества Х и У. Всякое множество f = (х; у) упорядоченных пар (х; у), х Х, у У, такое, что для любых пар (х; у) f и (х; у) f из условия уу следует, что х х, называется функцией, или, что то же самое, отображением из Х в У. В рассмотренном выше примере функция представляет собой следующее множество упорядоченных пар: f = (а; ), (b; ), (с; ), (d; ). Таким образом, функция есть не что иное, как спецификация подмножества декартова произведения Х  У. У.Множество всех первых элементов упорядоченных пар (х; у) некоторой функции f называется областью определения этой функции и обозначается Хf, а множество всех вторых элементов – множеством значений функции, которое обозначается Уf . Если f = (х; у) есть функция, то пишут f: Хf У и говорят, что f отображает множество Хf во множество У. В случае Х = Хf пишется просто f: ХУ. Если f: ХУ – функция и (х; у) f, то пишут у = f(х), а также f: х 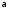 у, у, х Х, у У, и говорят, что функция f ставит в соответствие элементу х элемент у или, что тоже самое, элемент у соответствует элементу х. В этом случае говорят также, что элемент у является значением функции f в точке х или образом элемента х при отображении f. Иногда сама функция f обозначается символом f(х). Обозначение функции f:ХУ и ее значения в точке х Х одним и тем же символом f(х) обычно не приводит к недоразумению, так как в каждом конкретном случае, как правило, всегда бывает ясно, о чем именно идет речь. Обозначение f(х) часто оказывается удобнее обозначения f:х 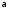 у при вычислениях. Например, запись f(х) = х2 удобнее и проще использовать при аналитических преобразованиях, чем запись f:х у при вычислениях. Например, запись f(х) = х2 удобнее и проще использовать при аналитических преобразованиях, чем запись f:х 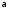 х2. х2.Вспомним еще, что бинарное отношение из множества Х во множество У мы определили как всякое подмножество декартова произведения Х  У. Таким образом, функция f:ХУ – это просто специальный вид бинарных отношений из Х в У, который удовлетворяет условию: для каждого х Х существует единственный у У такой, что (х; у) f. Подчеркнем, что один и тот же образ могут иметь несколько элементов области определения, и что не все элементы множества У обязаны быть образами некоторых элементов Х, т.е. множество значений функции Уf может совпадать с множеством У, а может быть его собственным подмножеством. У. Таким образом, функция f:ХУ – это просто специальный вид бинарных отношений из Х в У, который удовлетворяет условию: для каждого х Х существует единственный у У такой, что (х; у) f. Подчеркнем, что один и тот же образ могут иметь несколько элементов области определения, и что не все элементы множества У обязаны быть образами некоторых элементов Х, т.е. множество значений функции Уf может совпадать с множеством У, а может быть его собственным подмножеством.При заданном у У совокупность всех таких элементов х Х, что f(х) = у называется прообразом элемента у и обозначается f -1(у). Таким образом, f -1(у) = х х Х, f(х) = у. Очевидно, что если у У\ Уf, то f -1(у) = . Сюръекции, инъекции и биекции Пусть задано отображение f:Х У. Иначе говоря, каждому элементу х Х поставлен в соответствие и притом единственный элемент у У, и каждый элемент у Уf У поставлен в соответствие хотя бы одному элементу х Х. Если У=Х, то говорят, что отображение f отображает множество Х в себя. Если У= Уf , т.е. множество У совпадает с множеством значений функции f, то говорят, что f отображает множество Х на множество У, или что отображение f является сюръективным отображением, короче сюръекцией. Таким образом, отображение f:Х У есть сюръекция, если для любого элемента у У существует, по крайней мере, один такой элемент х Х, что f(х) = у. Если при отображении f:Х У разным элементам х Х соответствуют разные элементы у У, т.е. при х х имеет место f(х) f(х), то отображение f называется инъективным отображением или инъекцией. Таким образом, отображение f:Х У инъективно тогда и только тогда, когда прообраз каждого элемента у, принадлежащего множеству значений функции f, т.е. y  Уf, состоит в точности из одного элемента. Если отображение f:Х У является одновременно инъекцией и сюръекцией, то оно называется биективным отображением или биекцией. Уf, состоит в точности из одного элемента. Если отображение f:Х У является одновременно инъекцией и сюръекцией, то оно называется биективным отображением или биекцией. Примеры. Функция f:R R, f(х) = х2 не является ни инъекцией, ни сюръекцией, так как разным элементам, например, х = 2 и х = -2 соответствует одинаковый образ 4, и любое отрицательное действительное число не является образом ни для одного из элементов области определения. Функция f: a; b; c; d , , , , , заданная следующим образом: f(а) = , f(b) = , f(c)=  , f(d) = является инъективной и не является сюръективной. , f(d) = является инъективной и не является сюръективной.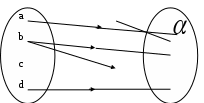 Эта функция инъективная, потому что у нее ни для одной пары элементов области определения образы не совпадают, но сюръекцией эта функция не является, потому что элемент множества У не является образом какого-либо элемента множества Х. С другой стороны, функция g:a; b; c; d; e ; ; ; , определенная так g(a) = , g(b) = , g(c) = , g(d) = , g(e) = является сюръективной и не является инъективной.   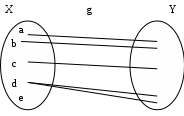 Эта функция сюръективна потому, что каждый элемент множества У является образом, по крайней мере, одного элемента из множества Х, но инъективной эта функция не является, потому что два элемента а и b области определения имеют один образ. На практике доказательство того, что заданная функция является инъективной, как правило, бывает проще производить, используя метод доказательства с помощью контрапозиции, согласно которого доказывается, что для всех хи х Х из равенства f(х)= f(х) следует, что х= х. Конечно, чтобы показать, что функция не является инъективной, нам достаточно найти контрпример, то есть найти два разных элемента х1 и х2 Х, у которых образы равны: f(х1) = f(х2). Любая линейная функция f:RR, f(x) = ax+b, (где а,b – фиксированные действительные числа, а0) является одновременно и инъективной и сюръективной, т.е. является биекцией. Чтобы показать, что f является инъекцией, мы должны показать, что для всех действительных чисел хи х из равенства f(х)= f(х) следует, что х= х. Итак, пусть f(х)= f(х) ах + b = ах + b ах= ах х= х, поэтому f – инъекция. Чтобы показать, что f – сюръекция, предположим, что у – любое действительное число. Мы должны найти х R такое, что f(х) = у. Пусть 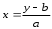 , ,тогда х R и 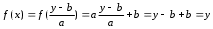 , ,поэтому f -сюръекция. Рассмотрим функцию f: Х У, где Х и У – подмножества R. Если у нас есть график функции у = f(х), то мы можем легко ответить на вопросы: является или нет функция f(х) инъективной или сюръективной?  Предположим, что f не инъективна. Тогда существуют два элемента хи х в Х такие, что х х, но f(х)= f(х) = b, то есть горизонтальная прямая у = b должна дважды пересечь график функции в точках, которые отвечают х = х и х = х. Предположим, что f не инъективна. Тогда существуют два элемента хи х в Х такие, что х х, но f(х)= f(х) = b, то есть горизонтальная прямая у = b должна дважды пересечь график функции в точках, которые отвечают х = х и х = х.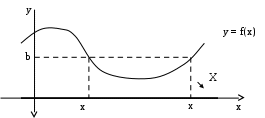 Если же f – инъективна, то такой ситуации никогда не возникнет, то есть горизонтальная прямая у = b, проведенная через любую точку b У на оси Оу, никогда не будет иметь с графиком функции более, чем одной общей точки. Если же f – сюръективна, то Уf = У, и любая горизонтальная прямая, проходящая через точку множества У, обязательно будет иметь общую с графиком точку. Проведенные рассуждения суммируем в виде следующей теоремы. Теорема 1. Пусть f:Х У – функция, где Х и У – подмножества R. Тогда: f – инъективна, если и только если каждая горизонтальная прямая, проходящая через точку b на оси Оу, будет иметь самое большее, одну общую точку с графиком f(х); f – сюръективна, если и только если каждая горизонтальная прямая, проходящая через точку b У оси Оу, будет иметь, по крайней мере, одну общую точку с графиком f(х). Примеры. 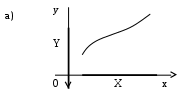 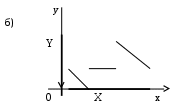 г) 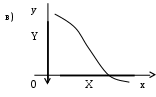 Ф 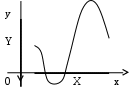 ункция с графиком (а) является инъективной, так как каждая горизонтальная прямая, проходящая через точку b оси OУ имеет не более, чем одну общую точку с графиком. Эта функция не является сюръективной, так как, например, горизонтальные прямые, проходящие через точки с отрицательными ординатама, не пересекают график функции ни разу. График (б) – это график функции, которая сюръективна, но не инъективна. Каждая горизонтальная прямая, проходящая через точки У, обязательно имеет хотя бы одну общую точку с графиком. Однако, у самой функции имеется горизонтальный участок, поэтому при соответствующем значении у горизонтальная прямая будет иметь бесконечно много общих точек с графиком. Аналогичные рассуждения показывают, что функция, представленная на графике (в), будет одновременно и инъективна и сюръективна, т.е. является биекцией, а функция, изображенная на графике (г), одновременно не является ни инъективной, ни сюръективной. Если f:Х У и А Х, то множество S = ууУ, у = f(х), х А, т.е. множество всех тех у, в каждый из которых при отображении f отображается хотя бы один элемент из подмножества А множества Х, называется образом подмножества А и обозначается S = f(А). В частности, всегда Уf = f(X). Для образов множеств А  Х и В Х и В  Х справедливы следующие соотношения: Х справедливы следующие соотношения:f(АВ) = f(А)f(B), f(АВ) f(А)f(B), f(А)\f(В) f(А\В), и если АВ, то f(А)f(В). Если f:Х У и SУ, то множество А = ххХ, f(х)S называется прообразом множества S и обозначается А=f -1(S). Таким образом, прообраз множества S состоит из всех тех элементов хХ, которые при отображении f отображаются в элементы из S, или, что то же самое, которое состоит из всех прообразов элементов уS, т.е. f -1(S) = 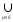 f- -1(у). Для прообразов множеств SУ и ТУ справедливы соотношения: f- -1(у). Для прообразов множеств SУ и ТУ справедливы соотношения:f -1(S Т) = f -1(S) f -1(Т) f -1(S Т) = f -1(S) f -1(Т) f -1(S \ Т) = f -1(S) \ f -1(Т), а если SТ, то f -1(S) f -1(Т). Если АХ, то функция f:Х У естественным образом порождает функцию, определенную на множестве А, ставящую в соответствие каждому элементу хА элемент f(х). Эта функция называется сужением функции f на множестве А и иногда обозначается fА. Таким образом, fА: АУ и для любого хА имеет место fА: х 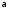 f(х). Если множество А не совпадает со множеством Х, то сужение fА функции f на множестве А имеет другую область определения, чем функция f, и, следовательно, является другой, чем f, функцией. f(х). Если множество А не совпадает со множеством Х, то сужение fА функции f на множестве А имеет другую область определения, чем функция f, и, следовательно, является другой, чем f, функцией.Композиция функций Пусть f:ХУ и g:УZ – функции. Функция F:XZ, определенная для каждого хХ формулой F(x)=g(f(x)) называется композицией (суперпозицией) функций f и g, или сложной функцией, и обозначается  . . Композицию функций  можно проиллюстрировать следующим образом: можно проиллюстрировать следующим образом: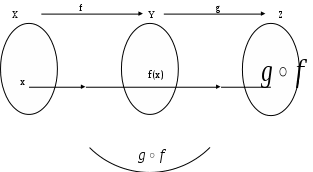 Пример. Пусть Х= a; b; c; d; e, У= ; ; ; , Z= 1; 2; 3; 4; 5; 6. Пусть f:Х У и g:УZ – функции, определенные соответственно так: f(a) = , f(b) = , f(c) = f(d) = f(e) = ; g() = 3, g() = g() = 5, g() = 1. 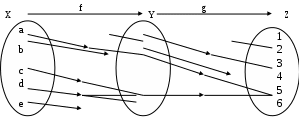 Тогда композиция функций  : ХZ будет: а : ХZ будет: а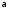 5, b 5, b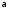 3, с 3, с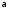 5, d 5, d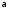 5, e 5, e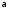 5. 5.Заметим, что множество значений композиции  является подмножеством множества значений функции g, т.е. имеет место является подмножеством множества значений функции g, т.е. имеет местоТеорема 2. Пусть :ХУ и g:УZ. Тогда (  ) (Х) g (У) или ) (Х) g (У) или 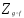 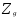 . . Доказательство. Пусть z (g  f) (X), тогда существует хХ такой, что f) (X), тогда существует хХ такой, что (  )(х) = g(f(x)) = z. Пусть у=(х)У, тогда g(y) =z, поэтому zg(Y) и теорема доказана. )(х) = g(f(x)) = z. Пусть у=(х)У, тогда g(y) =z, поэтому zg(Y) и теорема доказана.Теорема 3. Пусть даны две функции f:ХУ и g:УZ. Тогда если f и g обе инъективны, то композиция  также инъективна, а если f и g обе сюръективны, то и композиция также инъективна, а если f и g обе сюръективны, то и композиция  также сюръективна. также сюръективна.Доказательство. Пусть f и g – инъективны. Пусть х, хХ, у=f(x), у=f(x). Тогда из равенства (  )(х) = ( )(х) = ( ) (х) следует, что g(f(x)) = g(f(x)) или g(y) = g(у) у = у (так как g инъективна) f(x) = f(x) (так как у = f(x), у = f(x) х = х (так как f инъективна), следовательно ) (х) следует, что g(f(x)) = g(f(x)) или g(y) = g(у) у = у (так как g инъективна) f(x) = f(x) (так как у = f(x), у = f(x) х = х (так как f инъективна), следовательно  – инъективна. – инъективна.Пусть f и g сюръективны и z Z. Так как g сюръективна, то существует у У такой, что g(y) = z, и так как f сюръективна, то существует х Х такой, что f(x) = у. Следовательно, существует х Х такой, что (  ) (х) = g(f(x)) = g(y) = z, поэтому ) (х) = g(f(x)) = g(y) = z, поэтому  сюръективна. сюръективна.Можно показать, что обратное утверждение не имеет места, то есть если композиция  инъективна (сюръективна), то отсюда не следует, что f и g с неизбежностью являются инъективными (сюръективными). Для этого приведем следующий пример: инъективна (сюръективна), то отсюда не следует, что f и g с неизбежностью являются инъективными (сюръективными). Для этого приведем следующий пример:Пусть Х= х1; х2, У= у1; у2; у3, Z = z1; z2 и определим f:ХУ, f(х1) = у1, f(х2) = у2; g:УZ, g(у1) = Z1, g(у2) = g(у3) = Z2: Я 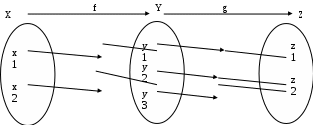 сно, что f – инъективна, но не сюръективна; g – сюръективна, но не инъективна, тем не менее композиция (  ):ХZ дает ( ):ХZ дает ( )(х1) = z1, ( )(х1) = z1, ( )(х2) = z2, то есть )(х2) = z2, то есть  одновременно и инъективна, и сюръективна. одновременно и инъективна, и сюръективна.Рассмотренный пример приводит к следующей теореме: Теорема 4. Пусть даны две функции f:ХУ и g:УZ. Тогда если композиция  инъективна, то f также инъективна, а если композиция инъективна, то f также инъективна, а если композиция  сюръективна, то g также сюръективна. сюръективна, то g также сюръективна.Доказательство. В обоих случаях применим метод доказательства с помощью контрапозиции. В первом случае высказывание контрапозиции будет следующим: если f – неинъективная, то и композиция  – неинъективная. Предположим, что f – неинъективная, тогда существуют х, хХ такие, что хх, но f(x) = f(x). – неинъективная. Предположим, что f – неинъективная, тогда существуют х, хХ такие, что хх, но f(x) = f(x). Следовательно, (  )(х) = (g f)(х), поэтому композиция функций также не инъективна. )(х) = (g f)(х), поэтому композиция функций также не инъективна.Во втором случае высказывание контрапозиции будет таким: если g несюръективна, то композиция  несюръективна. Предположим, что g несюръективна. Тогда множество значений этой функции g(У) является собственным подмножеством множества Z. Так как, по теореме 2, ( несюръективна. Предположим, что g несюръективна. Тогда множество значений этой функции g(У) является собственным подмножеством множества Z. Так как, по теореме 2, ( )(Х) g(Y), то ( )(Х) g(Y), то ( )(Х) есть также собственное подмножество множества Z, поэтому композиция )(Х) есть также собственное подмножество множества Z, поэтому композиция  не является сюръективной функцией. не является сюръективной функцией. |
