Курсовая работа. Курсовая работа Мисан. Реферат мисан Евгений Александрович Методы исследования плазменного факела, возникающего при воздействии импульсного лазерного излучения на поверхности металла
 Скачать 0.91 Mb. Скачать 0.91 Mb.
|
48 Вт/(м.К)) выбросы металла перемешиваются и выравниваются по высоте. Так формируется внешняя зона кратера при n < 6 -8.
1.2 мс (временная структура импульса - хаотическая, средняя интенсивность воздействовашего на поверхность металла излучения ФОРМИРОВАНИЕ кратера на поверхности метаЛлОВ при воздействии ИМПУЛЬСНОГО лазерного излучения УМЕРЕННОЙ ИНТЕНСИВНОСТИ В УСЛОВИЯХ ПЛАЗМООБРАЗОВАНИЯ Для исследования формы поверхности образовавшегося на пластине кратера использовался метод проекции полос [37], который в данном случае оказался более эффективным по сравнению с голографическими методами получения контуров рельефа, стереофотограмметрическим [38] и некоторыми другими методами [39 – 44], так как позволял ещё на стадии проецирования полос, получить картину с регулируемой чувствительностью измерений и достаточно хорошей видностью полос, контролируемых визуально. Регулирование чувствительности измерений (относительное смещение полосы) достигалось изменением периода спроецированных полос, а хорошая видность обеспечивалась изменением угла освещения исследуемой поверхности до устранения световых бликов от поверхности кратера. В работах [45, 46] для изучения деформаций поверхности были использованы муаровые методы. Однако, если точность интерференционных методов теоретически определяется длиной волны света, то для описанных муаровых методов при теоретической точности 25 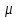 м наилучшее разрешение составляло м наилучшее разрешение составляло |
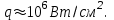 ), и сделаны некоторые предположения о начальной стадии формирования кратера.
), и сделаны некоторые предположения о начальной стадии формирования кратера.Целью настоящей работы является изучение формирования рельефа как внешней (наплавленной), так и внутренней (зоны разрушения) зоны кратера на поверхности металлов (In, Pb, Sn), облучаемых повторяющимися относительно короткими (несколько десятков наносекунд) гладкими лазерными импульсами с
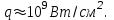
В качестве источника воздействующего на образец излучения использовался модуль, созданный на основе лазера ГОС-1001 (А = 1.06 мкм). Для получения моноимпульсного и импульсно-периодического режимов генерации применялись пассивные затворы из фтористого лития с
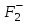 -центрами окраски . Управление частотой повторения лазерных импульсов в диапазоне 5-50 кГц осуществлялось изменением энергии накачки и оптической плотности пассивных затворов. Длительность отдельного пичка
-центрами окраски . Управление частотой повторения лазерных импульсов в диапазоне 5-50 кГц осуществлялось изменением энергии накачки и оптической плотности пассивных затворов. Длительность отдельного пичка 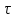 определялась параметрами резонатора и характеристиками используемого затвора и составляла 80 нс.
определялась параметрами резонатора и характеристиками используемого затвора и составляла 80 нс.Лазерное излучение при помощи фокусирующей системы направлялось на поверхность исследуемого образца. Сменные отражающие системы, включающие призму полного внутреннего отражения, позволяли направлять световой пучок на образец под произвольным углом, в том числе по нормали к нему, как вертикально (снизу вверх или сверху вниз), так и горизонтально.
Для получения на образце относительно однородного пятна фокусировки излучения с резкими границами диаметром d = 2.0 мм использовалась диафрагма диаметром 10 мм, изображение которой строилось фокусирующей системой на поверхности мишени. Часть (4%) энергии светового импульса, отраженная от передней грани стеклянного клина поступала на измеритель энергии ИМО-2Н, световой поток, отраженный от задней грани клина, направлялся на коаксиальный фотоэлемент ФЭК-15, что позволяло регистрировать временную форму лазерного импульса при помощи осциллографа С8-13. Энергия одного пичка изменялась от 2 до 6 Дж; временная форма его была близка к гауссовой; средняя интенсивность излучения в отдельном пичке составляла примерно (0.8-2.5)·109 Вт/см2. Суммарная энергия лазерного импульса варьировалась от 4 Дж (моноимпульс) до 150 Дж (35 пичков).
Для определения рельефа облучаемого образца нами использовался метод проекции полос [24], который был реализован на установке, описанной в работе [25], позволявший определять глубину (во внешней зоне - высоту h) любой точки кратера по отношению к необлученной плоской поверхности мишени с погрешностью, не превышающей 50 мкм. На рис. 2.4а,б представлены фотографии кратеров, полученных при воздействии на поверхность индиевой мишени лазерных импульсов, с числом пичков п = 4 . Внутренняя, или «отрицательная», зона кратера (откуда металл выносился в ходе воздействия лазерного излучения) имеет довольно ровную куполообразную поверхность (менее шероховатую, чем в [67]), причем как глубина зоны, так и ее диаметр при п — 30 больше, чем при п — 4. Внешняя, или «положительная», зона (на которую вынесенный металл наплавлен) имеет форму, близкую к округлой.
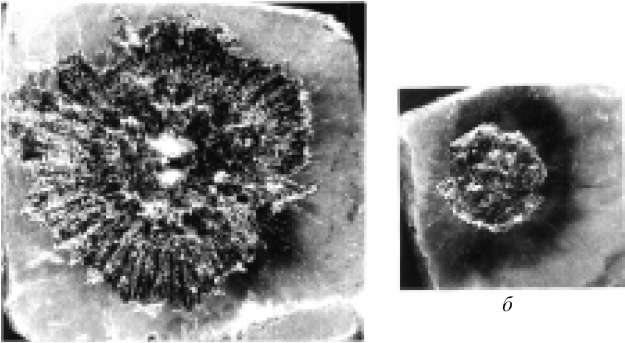
Рисунок 2.4 – Фотографии кратеров, полученных при воздействии 4) лазерных импульсов.
Следует отметить, что при воздействии излучения на вещество горизонтально или сверху вниз для п > 6 — 8 внешняя зона представляет собой набор округлых выбросов толщиной от 50 до 250 мкм, наплавленных друг на друга. Значение n, начиная с которого наблюдается наслоение выбросов друг на друга, определяется энергиями n-го и (n - 1)-го пичков. При воздействии лазерного излучения снизу вверх наслоение выбросов не наблюдалось. На краю каждого округлого выброса имелся небольшой (высотой не более 100 мкм) буртик. На рис.2.5 приведены зависимости характерных поперечных размеров наиболее крупного выброса l1, обожженной плазменным факелом зоны на поверхности облученного вещества l2 и внутренней зоны кратера l0, а также глубины внутренней зоны h0 от числа пичков п в лазерном импульсе.
На «внешних» выбросах (в случае воздействия снизу вверх - на периферии единственного выброса), а также на поверхности образца за пределами наиболее крупного округлого выброса имеются наплавленные «лучи». Исследования поверхности кратера при помощи оптического микроскопа показали, что указанные «лучи» представляют собой цепочки отдельных достаточно крупных (диаметром от 100 до 500 мкм) капель. Более мелкие капли наблюдаются и вне «лучей», в том числе и на поверхности внешней зоны кратера. В таблице приведены распределения капель по размерам на поверхностях различных выбросов внешней зоны кратера.
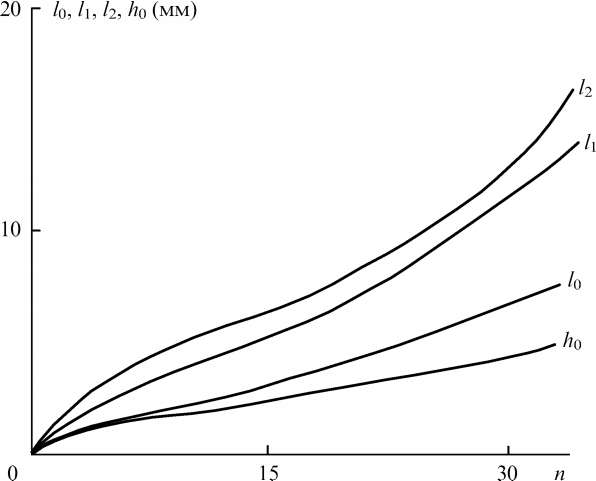
Рисунок 2.5 – Зависимости параметров кратера от числа пичков в воздействующем лазерном импульсе (лазерное излучение падает на индиевый образец сверху вниз).
Отметим, что размеры внешней зоны растут значительно быстрее, чем глубина и особенно диаметр внутренней зоны. При этом масса (и объем) внешней зоны кратера составляет примерно 80 % от массы (и объема) вынесенного материала. Обращает на себя внимание и то, что при воздействии лазерного излучения на образец снизу вверх размеры внешней зоны примерно в 1.5 раза больше, чем при воздействии в горизонтальном направлении и сверху вниз. Все это подтверждает то, что при рассматриваемом режиме воздействия световых импульсов на вещество внутренняя зона образуется за счет «выплескивания» (вытекания) материала из ванны расплава, а не за счет его испарения и тем более разбрызгивания (суммарная масса и объем капель составляют менее 1% от массы и объема вынесенного вещества). Это не противоречит данным работ и в то же время существенно отличается от результатов, полученных в [67], где внешняя зона формировалась в основном за счет разбрызгивания капель.
Для выяснения причин формирования кратеров с указанными формами нами был проведен расчет изменения температуры Т индиевого образца, облучаемого лазерными импульсами с использованными в эксперименте параметрами. Численно решалось уравнение:
 (2.2)
(2.2)с начальным условием
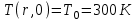 и граничным условием
и граничным условием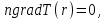 которое задавалось на реальной границе облучаемого образца - диска с толщиной I = 4 мм, радиусом R = 3 см и лункой на оси, имеющей форму сферического сегмента с радиусом кривизны
которое задавалось на реальной границе облучаемого образца - диска с толщиной I = 4 мм, радиусом R = 3 см и лункой на оси, имеющей форму сферического сегмента с радиусом кривизны 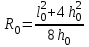 Диаметры и глубины лунок соответствовали диаметрам и глубинам внутренних зон кратеров, приведенных на рис.2.5. Функция источника
Диаметры и глубины лунок соответствовали диаметрам и глубинам внутренних зон кратеров, приведенных на рис.2.5. Функция источника 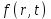 имела в пределах пятна фокусировки радиально симметричный вид:
имела в пределах пятна фокусировки радиально симметричный вид: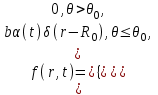 (2.3)
(2.3)где
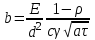 ,
, 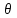 - полярный угол в сферической системе координат; Е = 2-6 Дж - энергия импульса; с = 240 Дж/(кг.К) - удельная теплоемкость индия [26]; d =2 мм - диаметр пятна фокусировки;
- полярный угол в сферической системе координат; Е = 2-6 Дж - энергия импульса; с = 240 Дж/(кг.К) - удельная теплоемкость индия [26]; d =2 мм - диаметр пятна фокусировки; 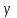 = 7.3.103 кг/м3-плотность индия [26]; а = 0.45 см2/с - температуропроводность индия ;
= 7.3.103 кг/м3-плотность индия [26]; а = 0.45 см2/с - температуропроводность индия ; 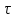 =80 нс;
=80 нс; 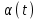 - нормированная энергия воздействующего лазерного импульса; коэффициент отражения
- нормированная энергия воздействующего лазерного импульса; коэффициент отражения 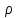 с учетом данных работ равнялся либо 0.8 (для твердого металла), либо 0.5 (для расплавленного металла);
с учетом данных работ равнялся либо 0.8 (для твердого металла), либо 0.5 (для расплавленного металла);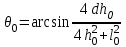 ,
, 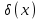 - дельта-функция Дирака.
- дельта-функция Дирака.Разумеется, подобная модель не учитывает затрат энергии на испарение и плавление металла, теплообмен с плазменным облаком и ряд других процессов, протекающих как в облучаемом образце, так и у его поверхности. Тем не менее, на наш взгляд, подобная модель может быть использована для качественного описания нагревания металла, по крайней мере в случае небольшого числа воздействующих на образец пичков (
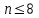 ).
).На рис.3 представлены рассчитанные для Е = 2 Дж временные зависимости
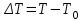 на границе пятна фокусировки излучения. Видно, что AT быстро (до окончания лазерного импульса) возрастает до значения, превышающего температуру плавления индия, и затем довольно быстро убывает (через
на границе пятна фокусировки излучения. Видно, что AT быстро (до окончания лазерного импульса) возрастает до значения, превышающего температуру плавления индия, и затем довольно быстро убывает (через 


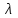 l = 0,6943 мкм), работавшего в режиме свободной генерации с энергией 10 Дж, сфокусированного в пятно площадью 4 мм2. Воспользовавшись данной картиной и учтя связь между смещением k тёмных полос и глубиной расположения точки интерференции относительно невозмущённой (плоской) поверхности образца [36]:
l = 0,6943 мкм), работавшего в режиме свободной генерации с энергией 10 Дж, сфокусированного в пятно площадью 4 мм2. Воспользовавшись данной картиной и учтя связь между смещением k тёмных полос и глубиной расположения точки интерференции относительно невозмущённой (плоской) поверхности образца [36]: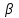 p + tg
p + tg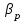 0,9 рад – угол между нормалью к поверхности образца и проецируемыми интерференционными поверхностями;
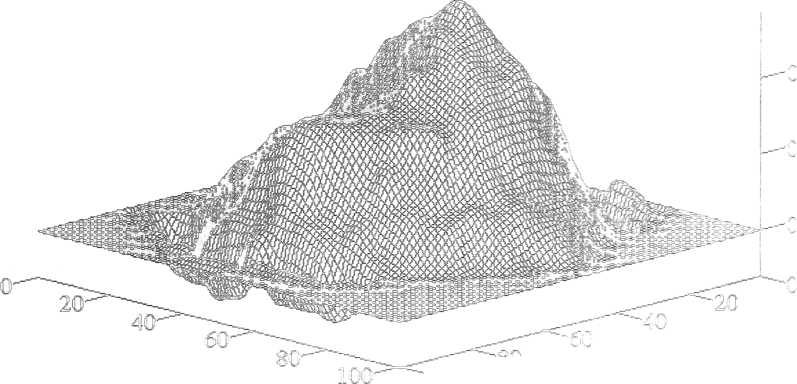
0,9 рад – угол между нормалью к поверхности образца и проецируемыми интерференционными поверхностями; 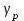 – угол между нормалью к поверхности образца и направлением наблюдения (оптической осью фотографической системы). При обработке картины контурных полос поверхности кратера (рисунок 2.2 а) относительная погрешность определения их смещения была 10 % (значительно превышала погрешность определения углов), что позволило определять глубину h1 при получении топограммы (рисунок 2.2 б) с абсолютной погшрешностью, не превышающей 25 мкм. На рисунке 2.3 представлено объемное (истинное (а) и инвертированное (б)) изображение того же кратера. Из рисунка 2.3 сразу видно, что кратер не только не симметричен, но и имеет весьма сложную форму. Рассчитанный по топограмме (рисунок 2.2 б) объём кратера V= 0,4 мм3 при максимальной глубине h= 0,3 мм. При замене его цилиндром той же глубины (модель плоского источника) объём получался бы существенно большим (0,9 мм3), как и при замене гиперболическим параболоидом (1,0 мм3). Если же моделирование проводить, опираясь на объём,
– угол между нормалью к поверхности образца и направлением наблюдения (оптической осью фотографической системы). При обработке картины контурных полос поверхности кратера (рисунок 2.2 а) относительная погрешность определения их смещения была 10 % (значительно превышала погрешность определения углов), что позволило определять глубину h1 при получении топограммы (рисунок 2.2 б) с абсолютной погшрешностью, не превышающей 25 мкм. На рисунке 2.3 представлено объемное (истинное (а) и инвертированное (б)) изображение того же кратера. Из рисунка 2.3 сразу видно, что кратер не только не симметричен, но и имеет весьма сложную форму. Рассчитанный по топограмме (рисунок 2.2 б) объём кратера V= 0,4 мм3 при максимальной глубине h= 0,3 мм. При замене его цилиндром той же глубины (модель плоского источника) объём получался бы существенно большим (0,9 мм3), как и при замене гиперболическим параболоидом (1,0 мм3). Если же моделирование проводить, опираясь на объём, 
 а).
а).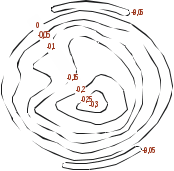 б).
б).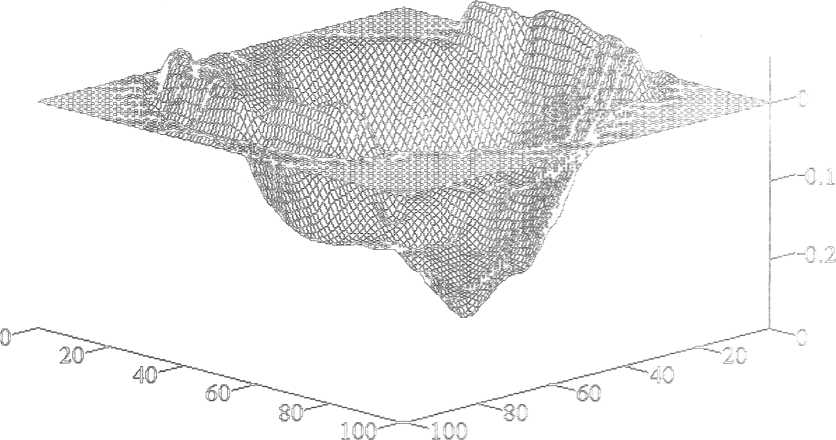
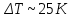 ). Существенно, что при подаче через 20 мкс 2-го лазерного пичка временная зависимость Δ
). Существенно, что при подаче через 20 мкс 2-го лазерного пичка временная зависимость Δ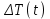 хорошо согласуются с полученными аналитически в рамках модели плоского теплового источника с тем же диаметром d и с
хорошо согласуются с полученными аналитически в рамках модели плоского теплового источника с тем же диаметром d и с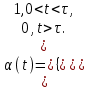 (2.4)
(2.4) 6 Дж при n > 6) до подачи следующего пичка металл не успевает кристаллизоваться и, вероятно,
6 Дж при n > 6) до подачи следующего пичка металл не успевает кристаллизоваться и, вероятно, 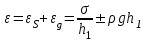 (2.6)
(2.6)