Реферат. Объемы тел вращения. Реферат Объёмы тел вращения. Реферат Объёмы тел вращения
 Скачать 3.95 Mb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ПЕНЗЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Кафедра «Математическое образование» Направление подготовки 44.03.01 Педагогическое образование Профиль подготовки Математика РЕФЕРАТ «Объёмы тел вращения» Выполнила: Яганина А.А гр. 15ФПМ-1 Проверила: Климова Татьяна Романовна Пенза, 2018 Тела вращения Тела вращения — объёмные тела, возникающие при вращении плоской геометрической фигуры, ограниченной кривой, вокруг оси, лежащей в той же плоскости Цилиндр Цилиндр — тело образованное вращением прямоугольника вокруг его стороны. На рисунке (1) изображен цилиндр, образованный вращением прямоугольника  вокруг  . - ось цилиндра . Стороны  и описывают равные круги, лежащие в параллельных плоскостях, их называют основаниями цилиндра. Радиусы кругов называют радиусами цилиндра. Сторона описывает поверхность, которую называют боковой поверхностью цилиндра. Отрезки боковой поверхности, равные и параллельные , называют образующими цилиндра.Высота цилиндра — отрезок, перпендикулярный основаниям, концы которого принадлежат основаниям. 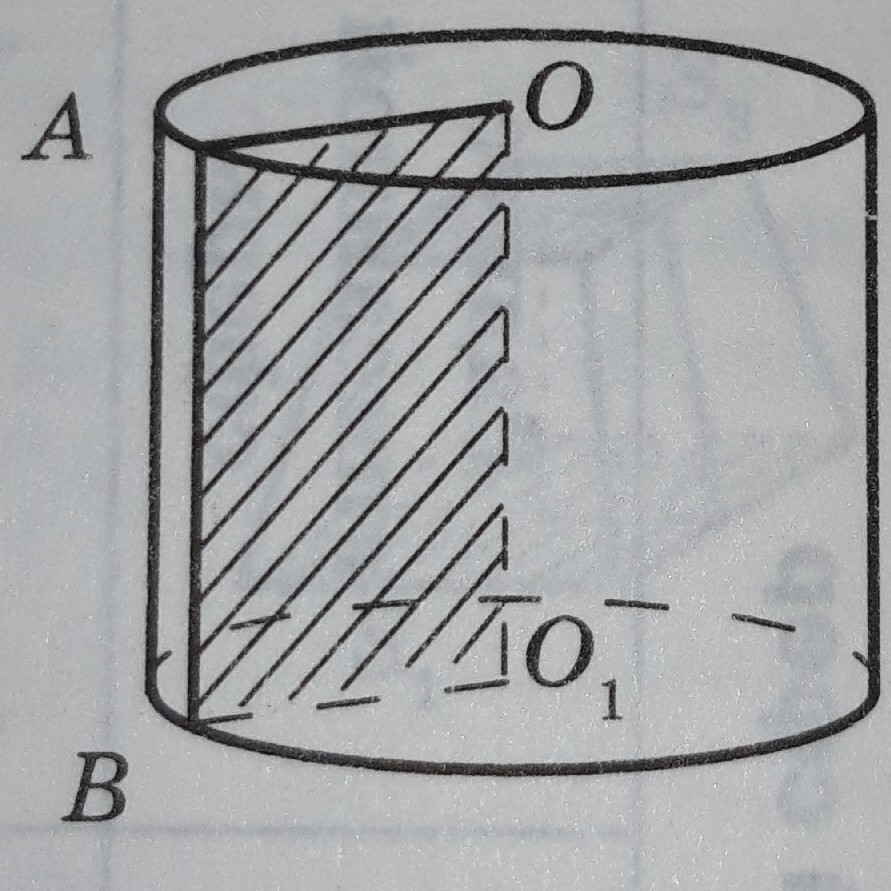 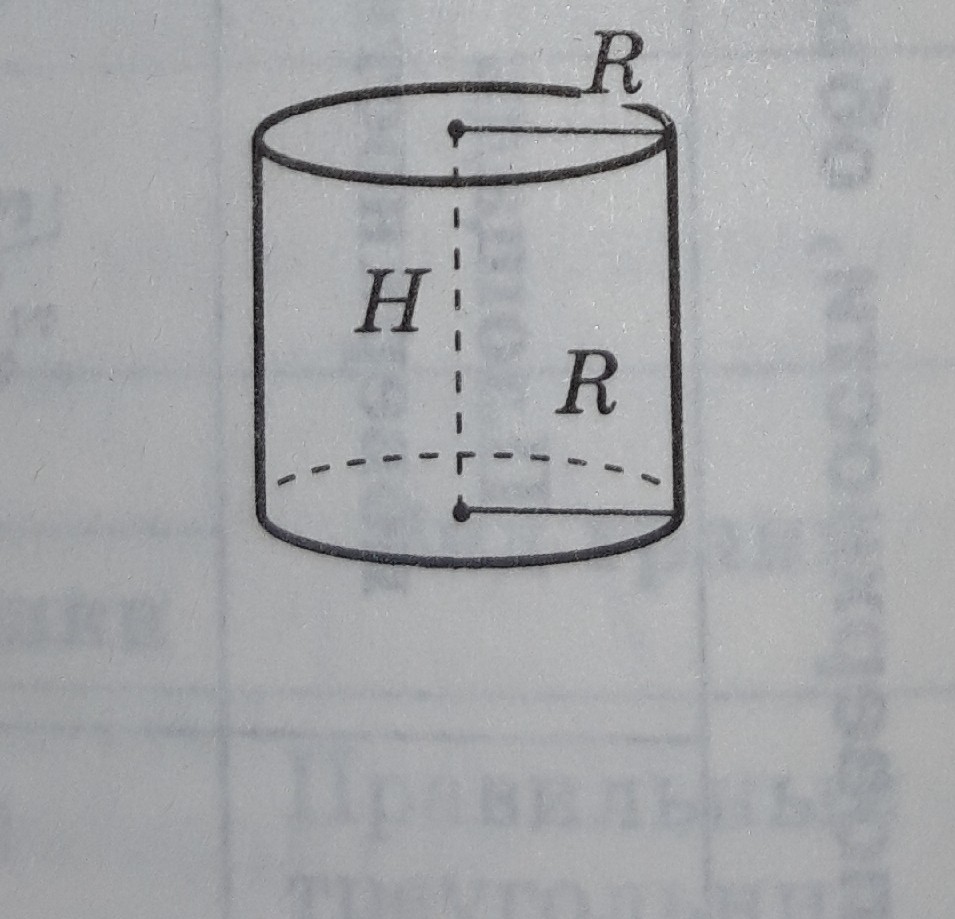 Рисунок (1) Рисунок 2 Площадь поверхности цилиндра Площадь поверхности цилиндра равна сумме площади боковой поверхности и площади основания.  ,  , где R — радиус основания цилиндра, Н — высота. Площадь боковой поверхности вычисляется по формуле:  Объем цилиндра Объём цилиндра равен произведению площади основания на высоту  , где R — радиус основания цилиндра, Н — высота. Конус Конус — тело, образованное вращением прямоугольного треугольника вокруг одного из его катетов. На рисунке (3) изображен конус, образованный вращением прямоугольного треугольника SAO вокруг катета SO. SO — ось конуса. Гипотенуза SA описывает боковую поверхность конуса, а катет AO — круг — основание конуса. Радиус этого круга называют радиусом конуса; точку S, отрезок SA, отрезок SO, прямую SO называют соответственно вершиной, образующей, высотой и осью конуса. 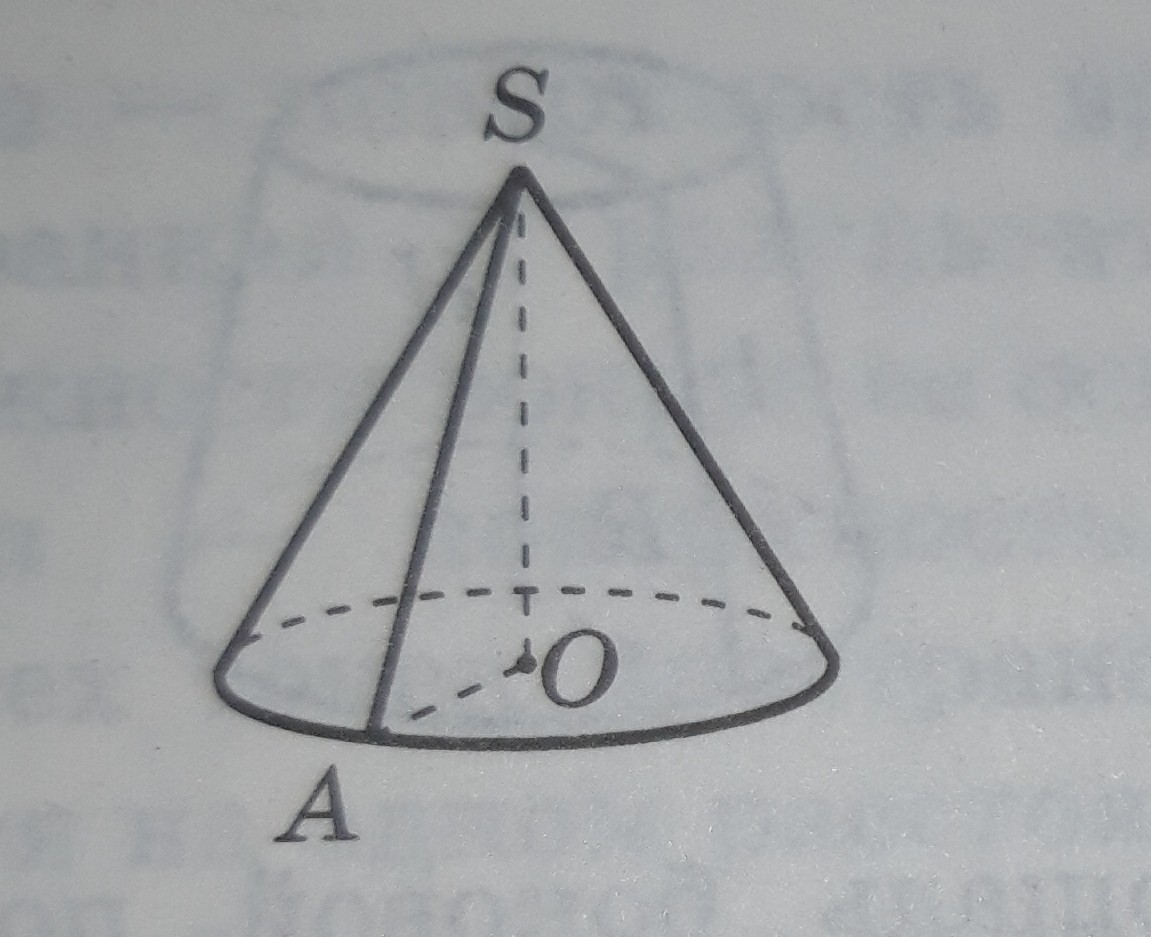 Рисунок 3 Площадь поверхности конуса Площадь боковой поверхности  ,где R — радиус основания конуса, l — образующая конуса. Площадь полной поверхности конуса ( площадь развертки ) 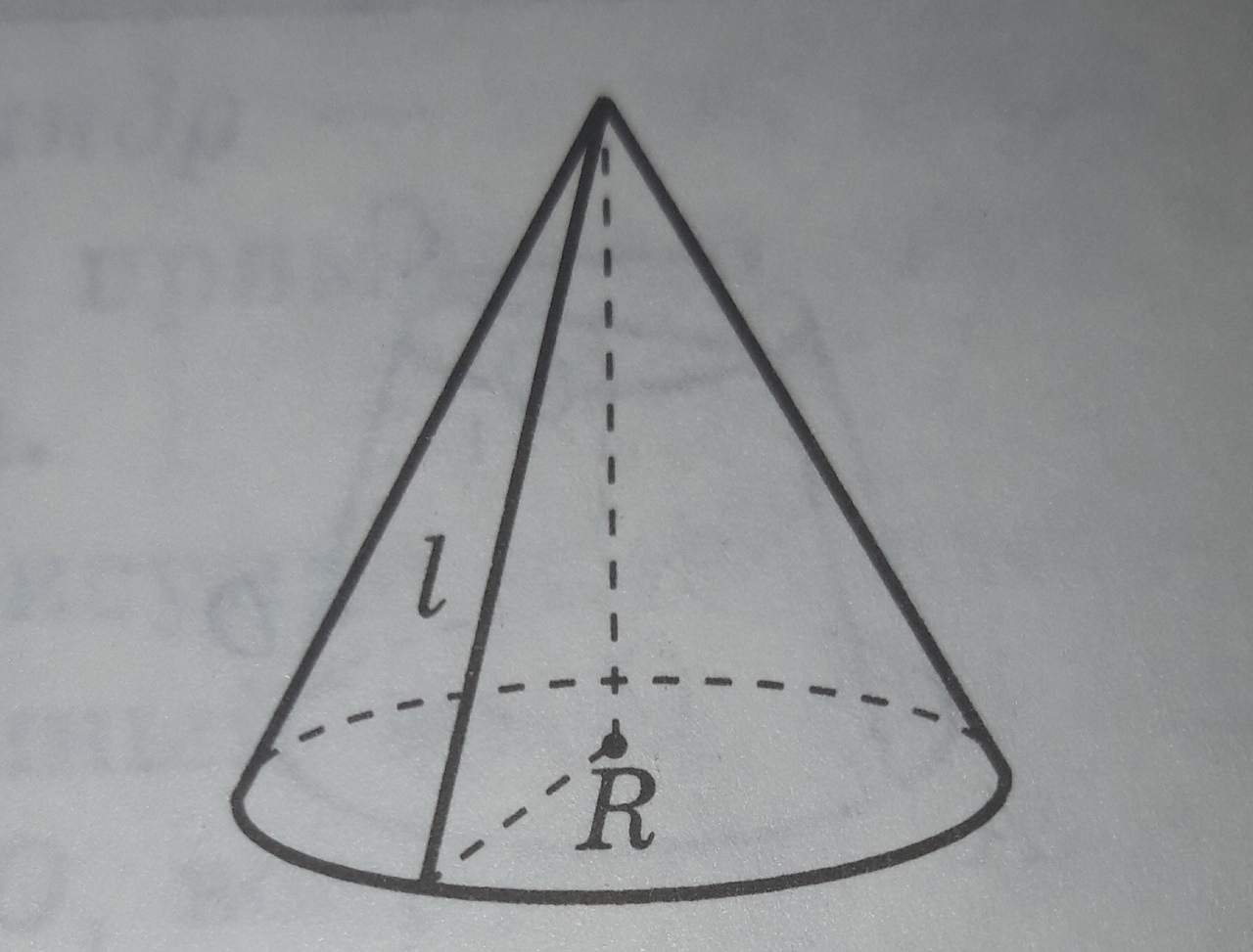 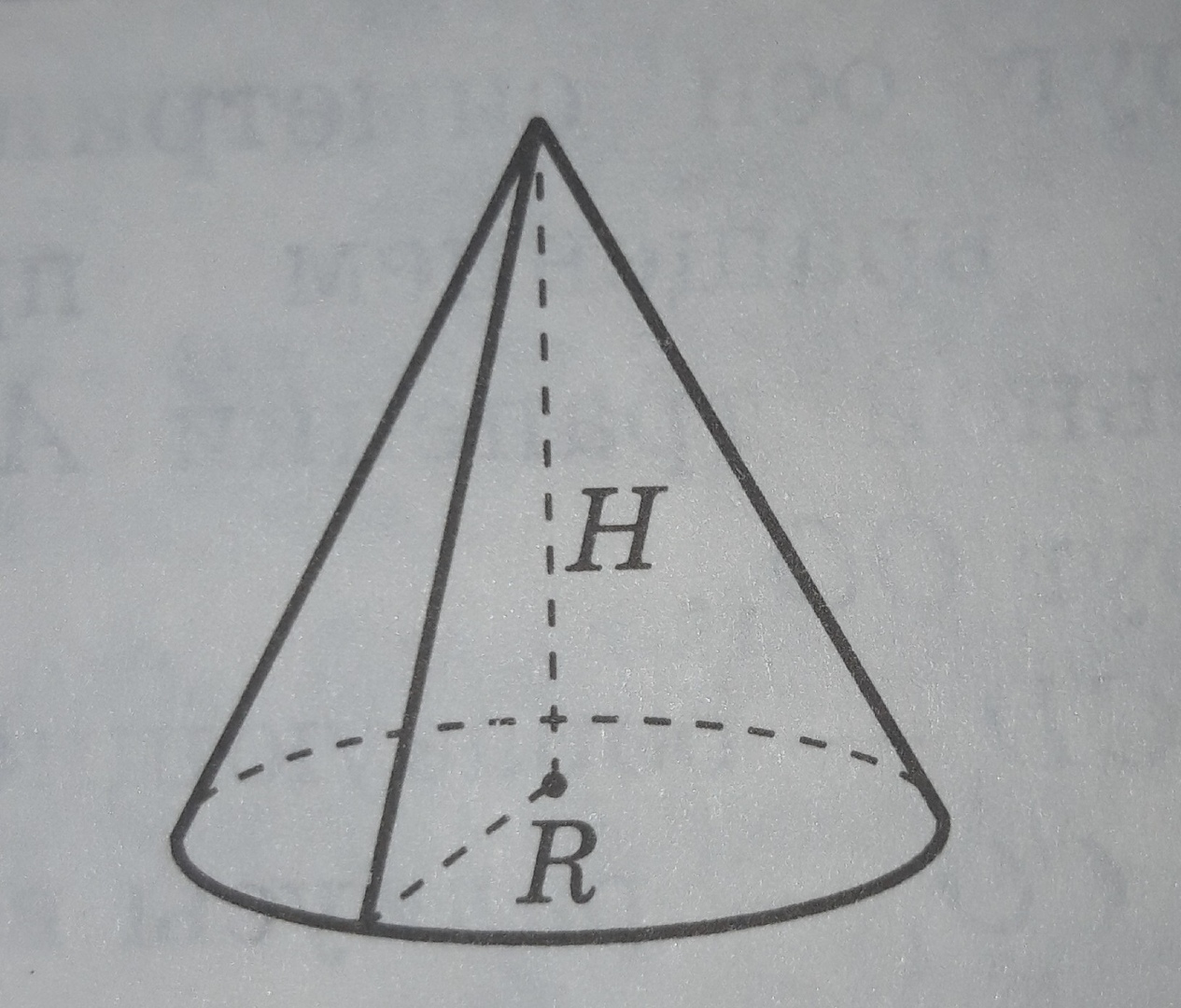  Объём конуса Объем конуса равен трети произведения площади основания на высоту конуса.  ,где R — радиус основания, Н — высота. Усеченный конус Усеченный конус — часть конуса, ограниченная его основанием и сечением, параллельным площади основания. Усеченный конус — тело вращения, образованное в результате вращения равнобедренной трапеции вокруг её оси симментрии или прямоугольной трапеции вокруг оси, содержащей боковую сторону, перпендикулярную основанию. На рисунке (6) изображен усеченный конус, образованный вращением равнобедренной трапеции  вокруг оси симметрии или вращением прямоугольной трапеции  вокруг . , - образующие;   - радиусы верхнего основания;AO, OD — радиусы нижнего основания . Высота усеченного конуса — расстояние между основаниями. 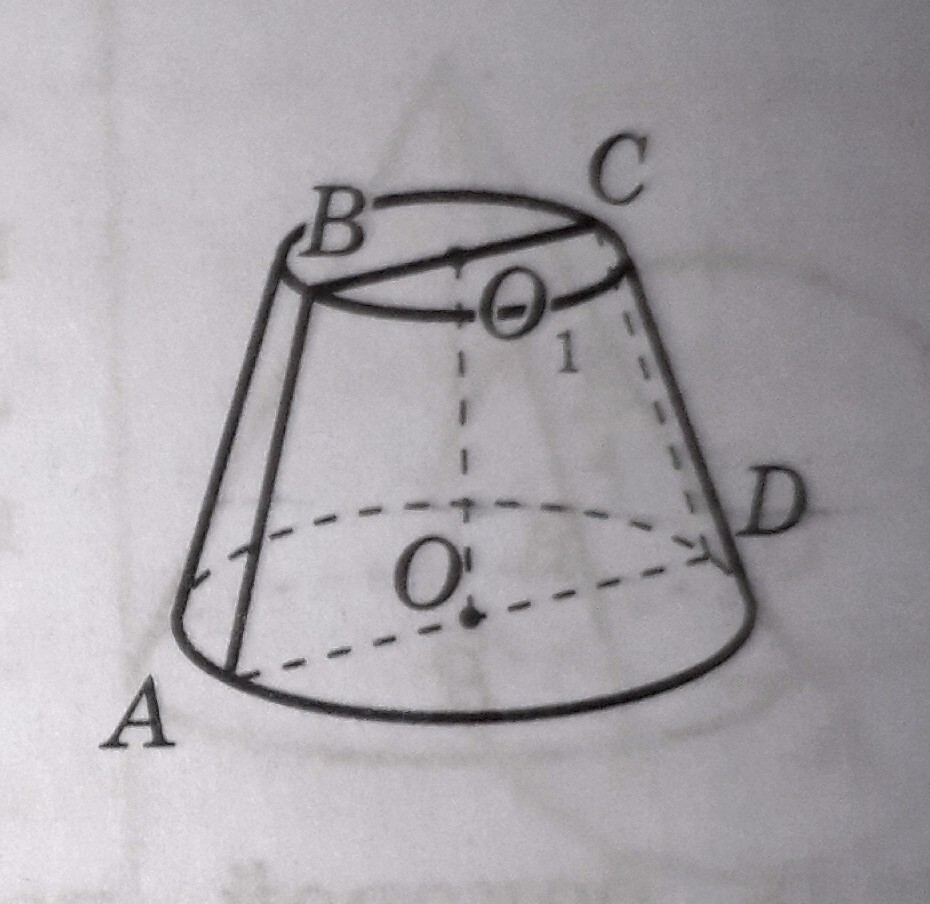- высота Рисунок 6 Площадь поверхности усечённого конуса Площадь боковой поверхности  ,где R, r — радиусы оснований усеченного конуса, l — образующая усечённого конуса. Площадь полной поверхности конуса  ,где 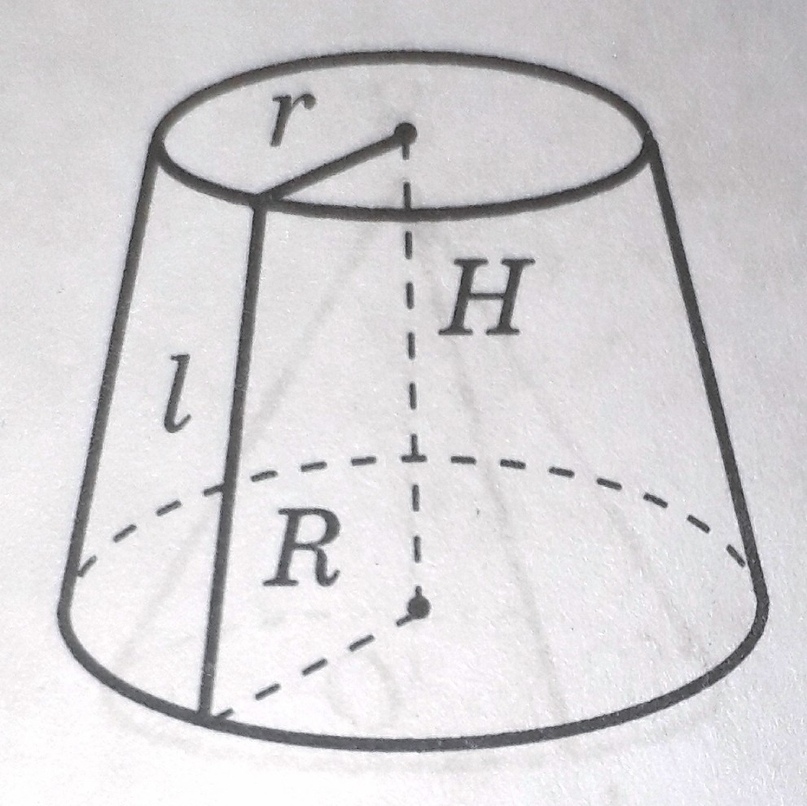 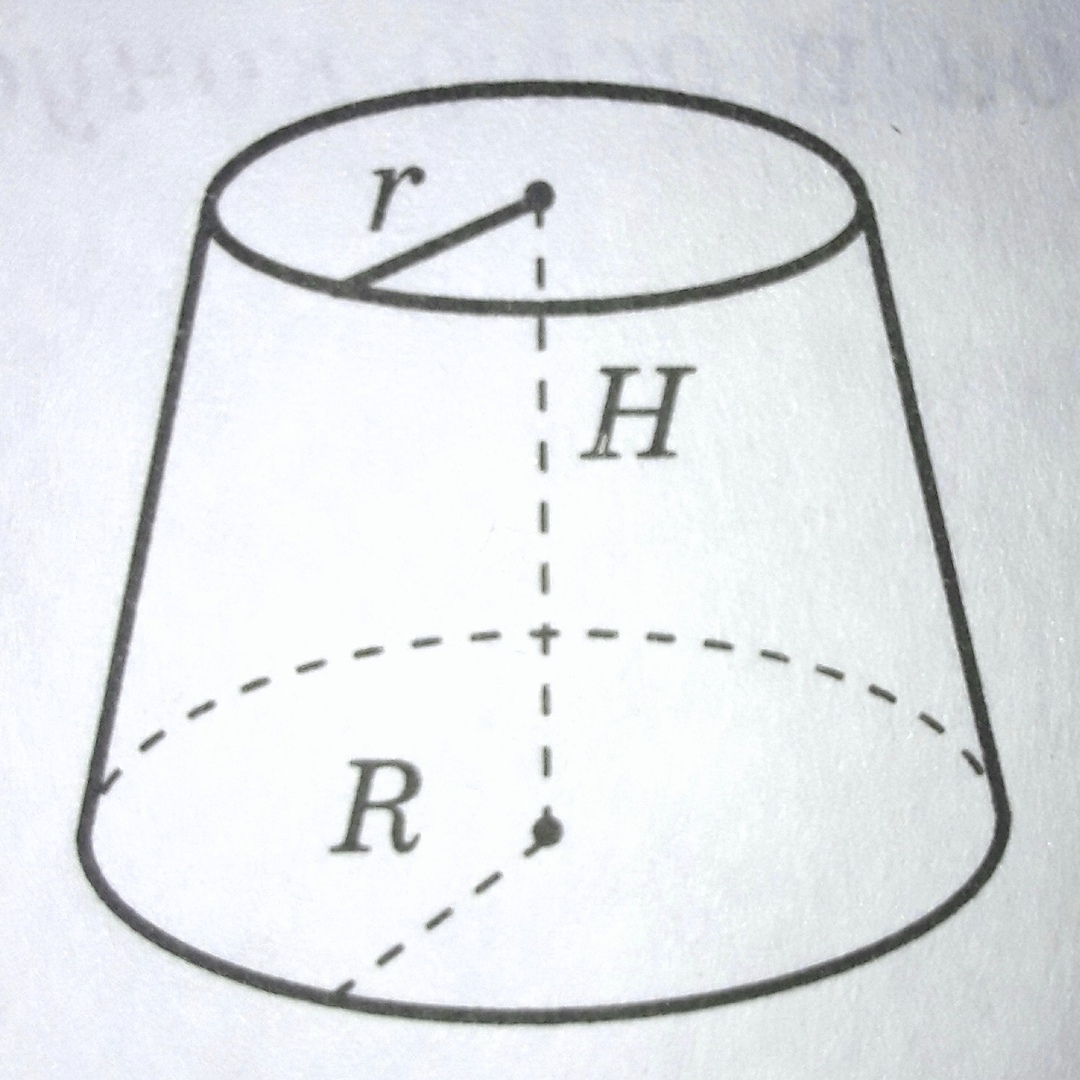, - площади оснований; R, r — радиусы оснований, l — образующая.  Объём усечённого конуса  , где R — радиусы оснований, Н — высота.Шар Шар — тело вращения, образованное в результате вращения полукруга вокруг прямой , содержащей диаметр, который ограничивает полукруг. Шар — тело, состоящее из всех точек пространства, находящихся на расстоянии, не большем данного (называемого радиусом) от данной точки (называемой центром) 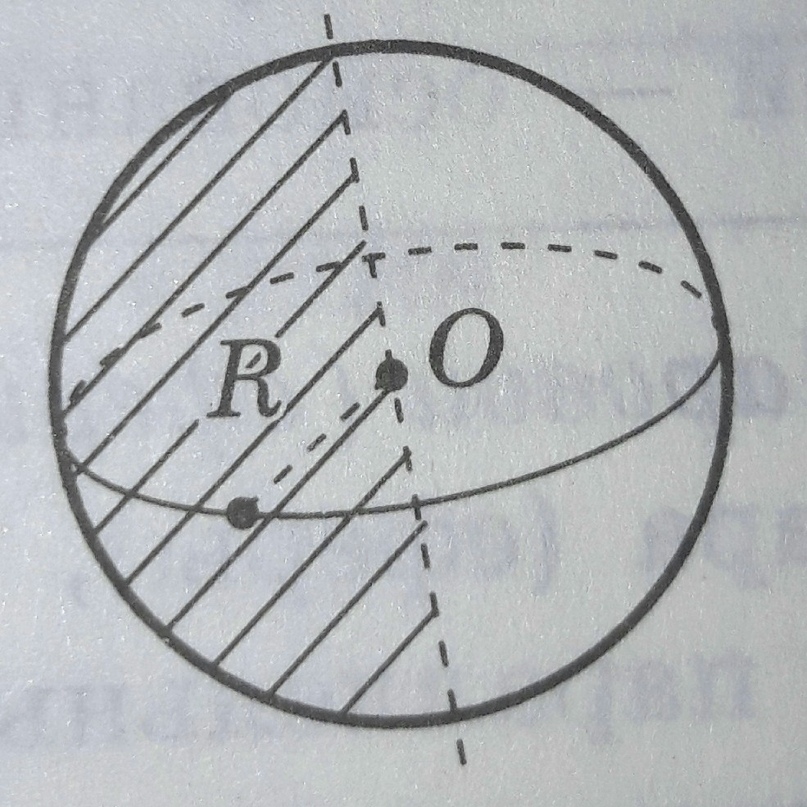 Объём шара Объём шара вычисляется по формуле  ,где R — радиус шара; d — диаметр шара.  Сфера Сфера — поверхность вращения, образованная в результате вращения окружности вокруг её оси симметрии. Сфера — поверхность, состоящая из всех точек пространства, находящихся на одном расстоянии (называемом радиусом) от данной точки (называемой центром). Диаметр сферы — отрезок, соединяющий две точки сферы и проходящий через ее центр. 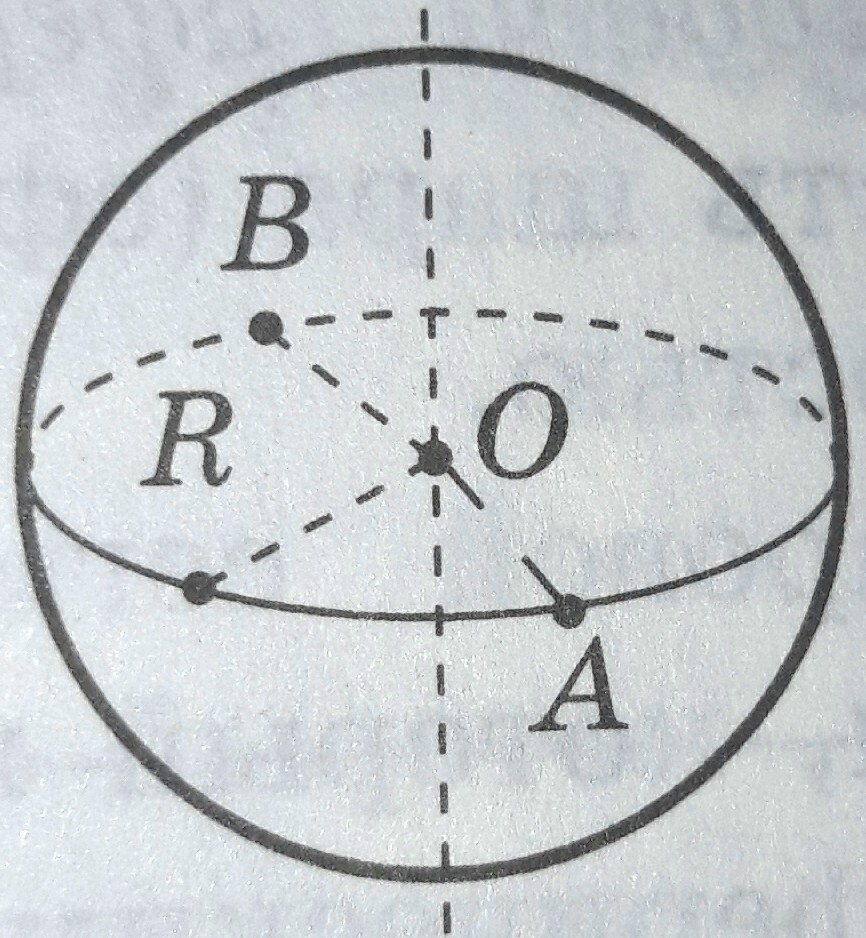 Площадь сферы Площадь сферы вычисляется по формуле  ,где R — радиус сферы; d — диаметр сферы. 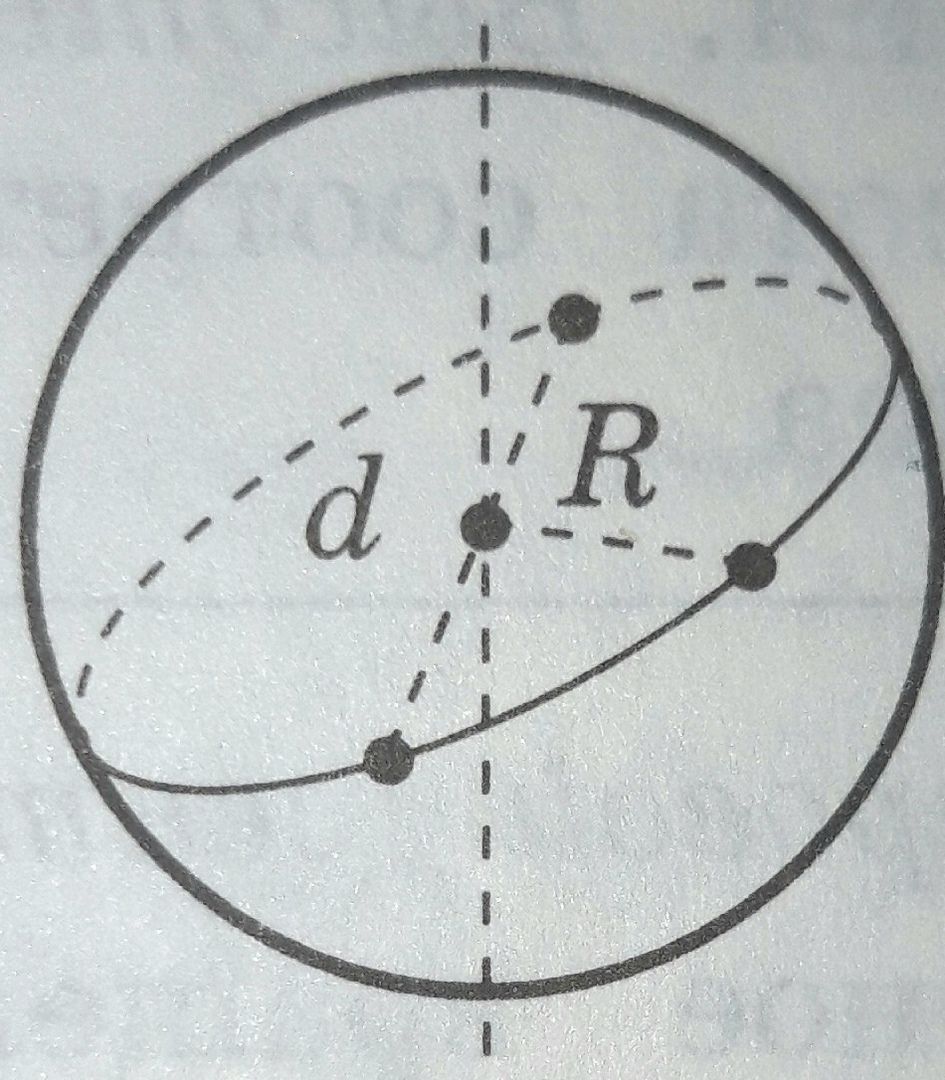 Шаровой сектор. Шаровой сегмент. Шаровой слой Шаровой сегмент Шаровой сегмент — часть шара, отсекаемая плоскостью. Круг, получающийся в сечении, называется основанием каждого из этих сегментов. Высота шарового сегмента — отрезок диаметра шара, перпендикулярного основанию шарового сегмента, один конец которого принадлежит сфере, а другой — основанию сегмента. 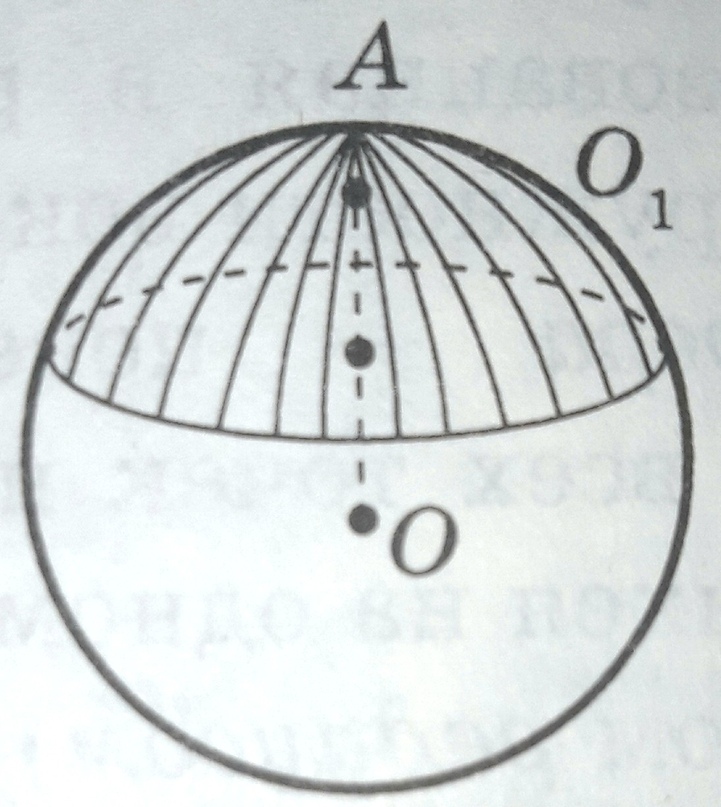  Площадь поверхности шарового сегмента   Объём шарового сегмента  Шаровой сектор Шаровой сектор — тело, образованное вращением кругового сектора вокруг оси, проходящей через центр. Высота шарового сектора — высота части его сферической поверхности. 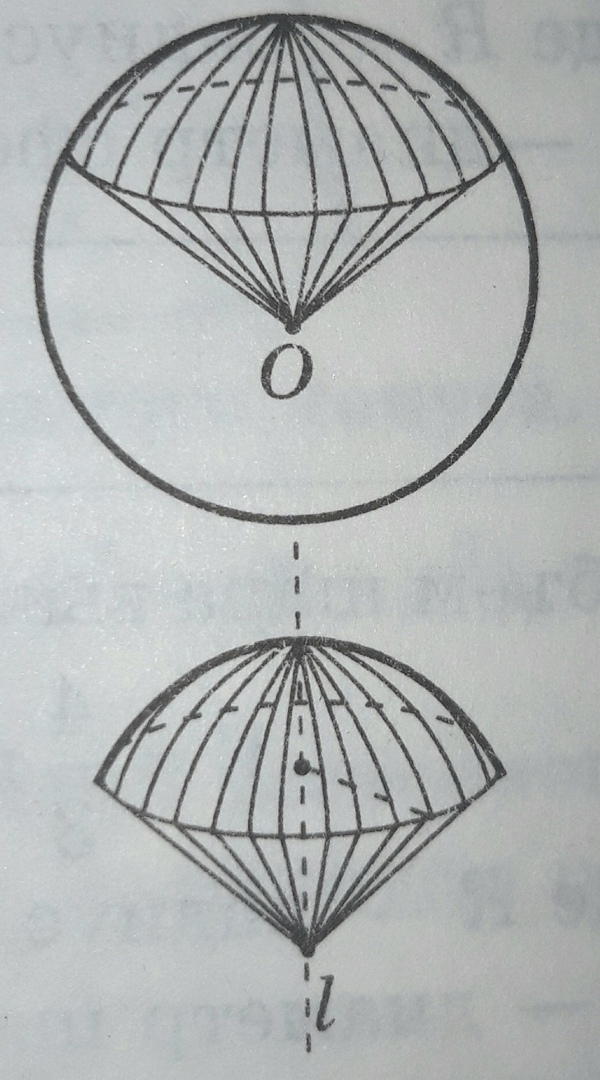 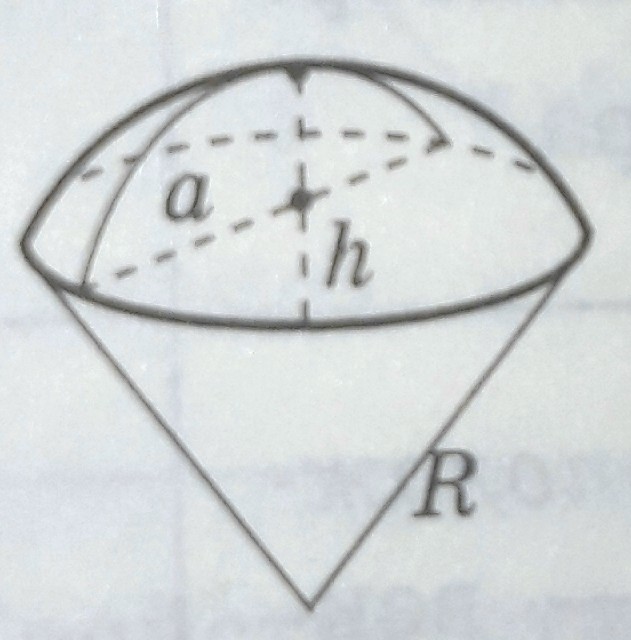 Площадь поверхности шарового сектора  , Объём шарового сектора  Шаровой слой Шаровой пояс — часть шара, расположенная между параллельными плоскостями, пересекающими шар. Шаровой пояс ограничен двумя кругами, называемыми основаниями. Высота шарового слоя — перпендикуляр, проведенный из точки одного основания к плоскости другого основания. 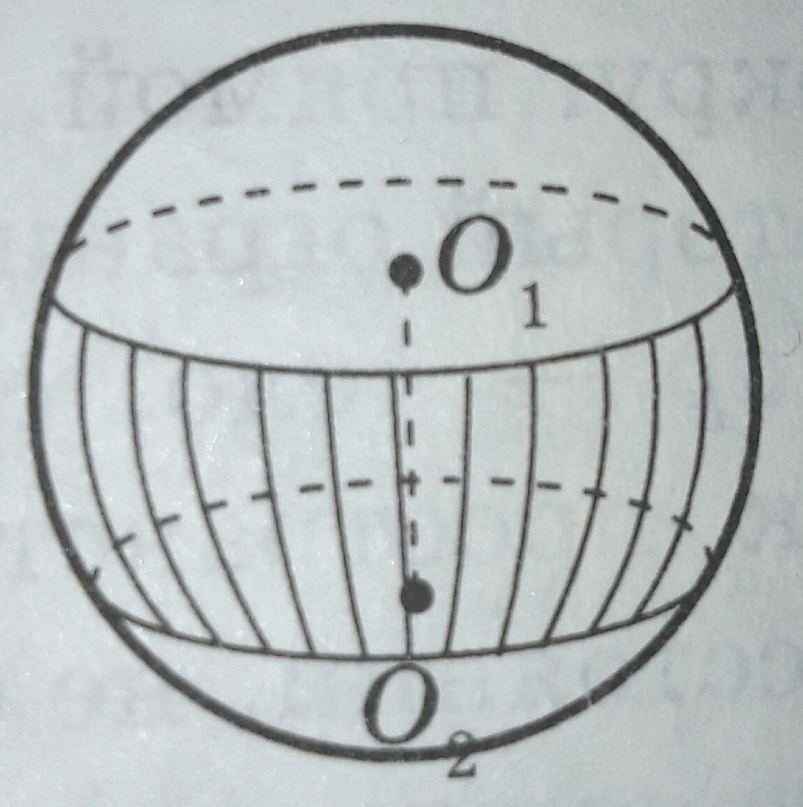 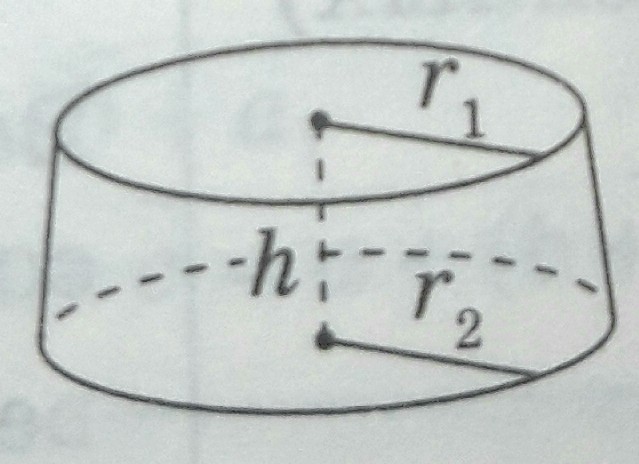 Площадь поверхности шарового пояса  Объём шарового пояса  Задания № 14, содержащиеся в ЕГЭ Задача №1. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки A, B и С, а на окружности другого основания — точка  , причём  — образующая цилиндра, а  — диаметр основания. Известно,что угол , , .а) Докажите,что угол между прямыми  и  равен 60° .б) Найдите объём цилиндра. Решение. 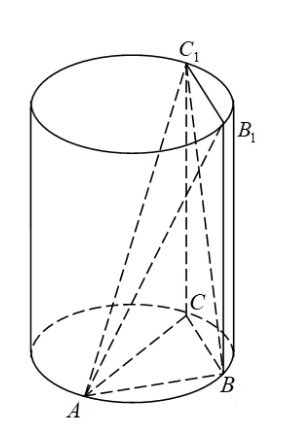 а) Пусть —  — образующая цилиндра. Тогда  — прямоугольник, поэтому угол между прямыми и равен углу .Угол ABC опирается на диаметр основания цилиндра, поэтому он прямой. Значит, прямая  , параллельная прямой , перпендикулярная прямым и . Таким образом, прямая перпендикулярна плоскости , а значит, угол прямой.В прямоугольном треугольнике : , .Значит,  .б) Отрезок AC является диаметром основания цилиндра. Значит,площадь основания цилиндра равна  .Следовательно, объём цилиндра равен  Ответ: б)  Задача №2 В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки A, B и C, а на окружности другого основания — точка  , причём — образующая цилиндра, а AC — диаметр основания. Известно,что , угол , , .а)Докажите,что угол между прямыми  и равен 45°.б)Найдите объём цилиндра. Решение. а) Пусть  — образующая цилиндра. Тогда — прямоугольник, поэтому угол между прямыми и равен углу .Угол ABC опирается на диаметр основания цилиндра, поэтому он прямой. Значит, прямая  , параллельная прямой , перпендикулярная прямым и Таким образом, прямая перпендикулярна плоскости , а значит, угол  прямой.В прямоугольном треугольнике : , .Значит, угол  .б) Отрезок AC является диаметром основания цилиндра. Значит,площадь основания цилиндра равна  Следовательно, объём цилиндра равен  Ответ: б) 4π Задача №3 Три образующие конуса попарно перпендикулярны, а длина каждого из них равна  . Найдите 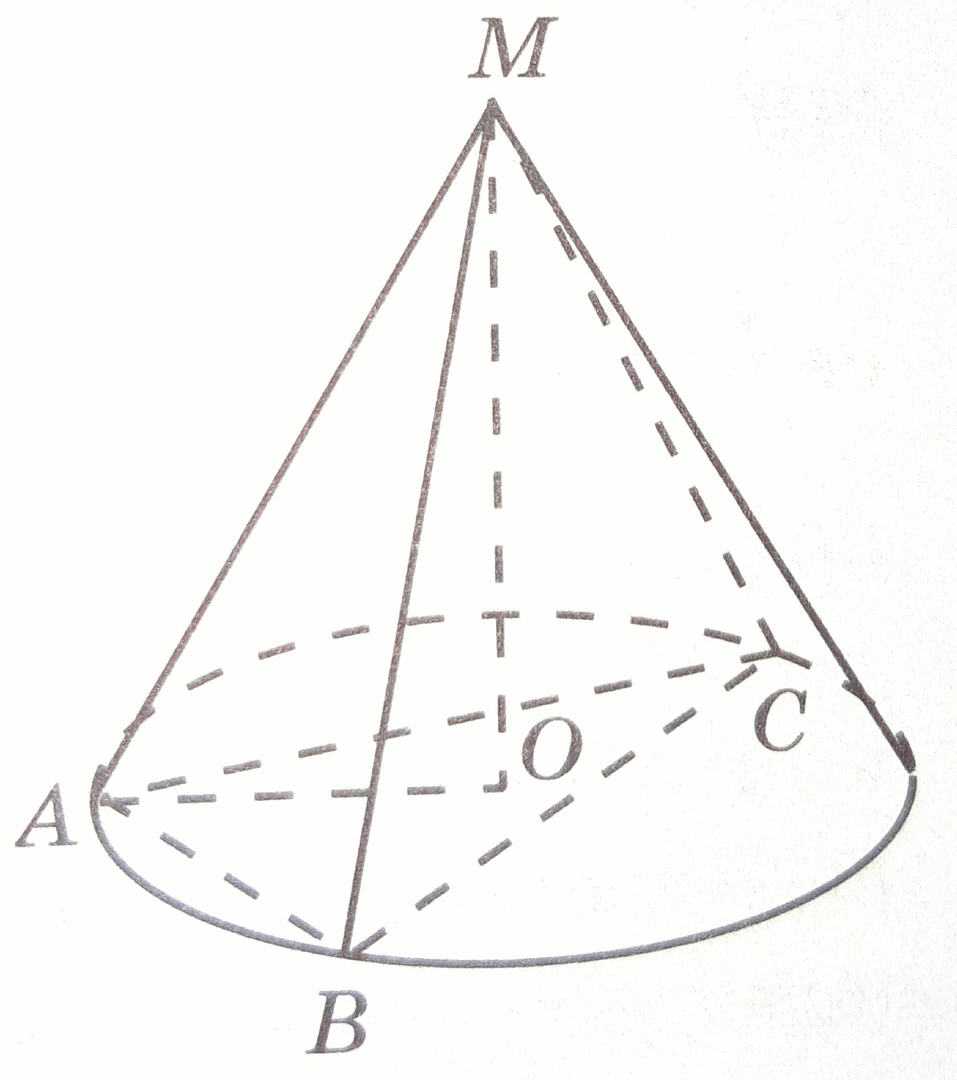объём конуса.Решение:  Пусть в конусе с вершиной М и центром основания О образующие АМ, ВМ и СМ попарно перпендикулярны. Следовательно треугольники АМВ, ВМС и СМА прямоугольные и равнобедренные, катеты которых соответственно равны. Поэтому это треугольники равны и, следовательно, равны их гипотенузы, т.е. АВ=ВС=СА. Поскольку по условию АМ=ВМ=СМ= , то АВ=ВС=СА=АМ = .Следовательно, треугольник АВС равносторонний со стороной, равной  . Поэтому радиус R конуса, равный радиусу окружности, описанной около равностороннего треугольника ABC, равен . Отсюда высота Н конуса может быть найдена из прямоугольного треугольника АОМ:  . Объём V конуса найдем по формуле  Ответ: 18π Задача №4 В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки  и , причем — образующая цилиндра, а отрезок пересекает ось цилиндра.а) Докажите, что угол  прямой.б) Найдите площадь боковой поверхности цилиндра, если AB = 20,  , Решение. а) Рассмотрим плоскость, проходящую через ось цилиндра и прямую . Обозначим точку пересечения этой плоскости и окружности основания цилиндра, содержащую точку А, через точку С. Тогда — образующая цилиндра. Отрезок АС пересекает ось цилиндра. Значит, он проходит через центр окружности основания цилиндра, то есть является ее диаметром. Следовательно угол АВС прямой.Прямая является образующей цилиндра, поэтому она перпендикулярна прямой АВ. Таким образом, прямая АВ перпендикулярна плоскости  а значит, угол прямой.б) Отрезок AC является диаметром основания цилиндра. Значит, длина окружности основания цилиндра равна  Следовательно, площадь боковой поверхности цилиндра равна  Ответ: б) 435 π |