Методы определения гранулометрического состава. Реферат По дисциплине Физика пласта (наименование учебной дисциплины согласно учебному плану)
 Скачать 1.45 Mb. Скачать 1.45 Mb.
|
|
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ  МИНИСТЕРСТВО науки и высшего ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования «САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ» Кафедра разработки и эксплуатации нефтяных и газовых месторождений Реферат По дисциплине Физика пласта (наименование учебной дисциплины согласно учебному плану) Тема работы: Методы определения гранулометрического состава Выполнил: студент гр. НГС 19 Выхристюк М.С. (шифр группы) (подпись) (Ф.И.О.) Оценка: Дата: Проверил руководитель работы: Сайченко Л.А. (должность) (подпись) (Ф.И.О.) Санкт-Петербург 2022 ОглавлениеВведение 4 Гранулометрический (механический) состав пород. 5 Ситовой 6 Седиментационный (оптический) 12 Седиментационный (весовой) 21 Гранулометрический анализ с помощью сканирующего электронного микроскопа 26 Заключение 29 Список использованной литературы 30 ВведениеГранулометрическим (механическим) составом породы называют количественное содержание в породе частиц различного размера, выраженное в весовых процентах. Гранулометрический анализ позволяет оценить степень дисперсности минеральных частиц, слагающих горную породу. Пески и слабосцементированные песчаники легко подвергается разделению зерен по фракциям. Сцементированные разности гранитных коллекторов изучают по шлифам под микроскопом. Иногда прибегают к дезинтеграции (разрушению) коллектора до зерен. От размеров частиц гранулярной среды зависит количество нефти, остающейся в пласте после завершения процесса разработки в виде пленок, покрывающих поверхность зерен или цементирующих компонентов среды, или в форме капиллярно удержанной нефти. Так же гранулометрическим состав может является причиной, осложняющей эксплуатацию скважины. Анализ размера частиц позволяет подобрать оптимальные фильтры, необходимые, для сдерживания механических примесей, поднимающихся вместе с добываемой продукцией, и предотвращения размыва породы вокруг скважины. Для улучшения понимания гидродинамических процессов и совершенствования технологий, необходимы создания новых методов, обеспечивающих анализ размеров частиц во всем диапазоне образца породы. Кроме того, физические принципы анализа должны коррелировать с физическими основами образования осадочных пород. Гранулометрический (механический) состав пород.Пласты, сложенные песками, состоят из разнообразных по размерам зерен неправильной формы. Количественное (массовое) содержание в породе частиц различной величины принято называть гранулометрическим (механическим) составом, от которого зависят многие свойства пористой среды: проницаемость, пористость, удельная поверхность, капиллярные свойства и т.д. По механическому составу можно судить о геологических и палеогеографических условиях отложения пород залежи. Поэтому начальным этапом исследований при изучении генезиса осадочных пород может быть гранулометрический анализ их. Так как размеры частиц песков обуславливают общую величину их поверхности, контактирующей с нефтью, от гранулометрического состава пород зависит количество нефти, остающейся в пласте после окончания его эксплуатации в виде пленок, покрывающих поверхность зерен. Гранулометрический состав песков важно знать в нефтепромысловой практике. Например, на основе механического анализа в процессе эксплуатации нефтяных месторождений для предотвращения поступления песка в скважину подбирают фильтры, устанавливаемые на забое [1]. Размер частиц пород изменяется от коллоидных частичек до галечника и валунов. Однако по результатам исследований размеры их для большинства нефтесодержащих пород колеблются в пределах 1 – 0,01 мм. Наряду с обычными зернистыми минералами в природе широко распространены глинистые и коллоидно-дисперсные минералы с размерами частиц меньше 0,1 мкм*(0,001 мм). Значительное количество их содержится в глинах, лёссах и других породах. В составе нефтесодержащих пород коллоидно-дисперсные минералы имеют подчиненное значение. Вместе с тем в следствие огромной величины их общей поверхности состав этих минералов влияет на процессы поглощения катионов (и анионов). От их количества в значительной степени зависит степень набухаемости горных пород в воде. В настоящее время имеются множество методов и способов определения гранулометрического состава породы. За последние десятилетия список дисперсных систем, применяемых для практических целей, все более и более расширяется. Поэтому необходимо определить те эффективные и подходящие методы, которые будут менее затратными и точными. Методы Прежде всего, необходимо рассмотреть простые и традиционные методы определения гранулометрического состава породы, выявить их основные принципы работы и рассмотреть их достоинства и недостатки. СитовойПервый метод, который будет рассмотрен – это ситовой. Большая часть технических сыпучих материалов представляют полидисперсные системы, частицы которых отличаются формой, размером и свойствами. Можно выделить наиболее фундаментальные характеристики, которые необходимо учитывать и регламентировать при описании движения сыпучих материалов, такие как размер и форма частиц, а также гранулометрический состав. Для определения содержания фракций частиц размером от 0,05 до 10 мм. Прибор для ситового анализа представляет собой несложную конструкцию. Под действием вращением вибраторов, создаются колебания. Набор которого состоит из 5 сит. Размеры отверстий сит - 2,0 мм; 1,0 мм; 0,5 мм; 0,25 мм; 0,094 мм. Сущность метода заключается в просеивании стандартной пробы через набор вибрирующих горизонтально расположенных сит с нормировано уменьшающимся характерным размером отверстий и в определении массы частиц каждого фракционного класса, задержавшегося на сите. Применительно к методу ситового анализа гранулометрического состава пробы полидисперсного материала его аналитическое описание при отсутствии учета реального содержания частиц каждой фракции в пробе представляется проблематичным. Для аналитического описания гранулометрического состава полидисперсных материалов, подвергшихся измельчению, используют или закон логарифмического нормального распределения (1) 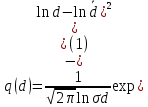 или закон нормального распределения Гаусса (2) 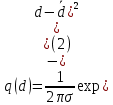 где – среднее квадратичное отклонение размера от статистического среднемассового размера; d – текущий (непрерывный) эквивалентный размер частиц, мкм; d – среднестатистический среднемассовый размер, мкм. Для проверки адекватности аналитического описания гранулометрического состава полидисперсного продукта проведены экспериментальные исследования состава измельченного в планетарной шаровой мельнице сыпучего материала методом ситового анализа. В качестве твердого зернистого материала использовалось пшено с начальной крупностью зерна 2,07 мм. В табл. 1 представлены основные технологические параметры режима измельчения. Рассев проб измельченного материала проводился на виброситах «УРЛ». Диапазон изменения калибра ячеек набора из пяти сит составлял 0,106 – 0,264 мм. Результаты исследований усреднялись по трем параллельным опытам и сведены в табл. 2. Таблица 1. Основные технологические параметры режима измельчения в планетарной шаровой мельнице «Активатор-2SL»
Таблица 2. Основные технологические параметры режима измельчения в планетарной шаровой мельнице «Активатор-2SL»
Обработка результатов исследований. На рис. 1 представлены гистограммы экспериментального распределения поверхностного и фракционного состава частиц после помола. Результаты рассева показывают преобладание в пробах мелких частиц, размером менее 1мм. 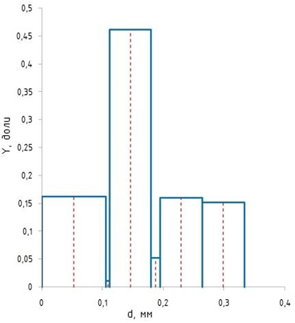 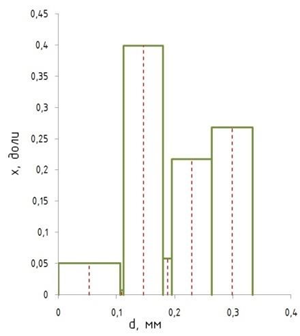 а б Рис. 1. Гистограмма экспериментального распределения состава частиц после помола: а - поверхностный; б – гранулометрический. На рис. 2 представлена гистограмма экспериментального распределения частиц полидисперсного материала в пробе и графики аналитического описания их законом нормального распределения Гаусса (1) и логарифмического нормального распределения (2). 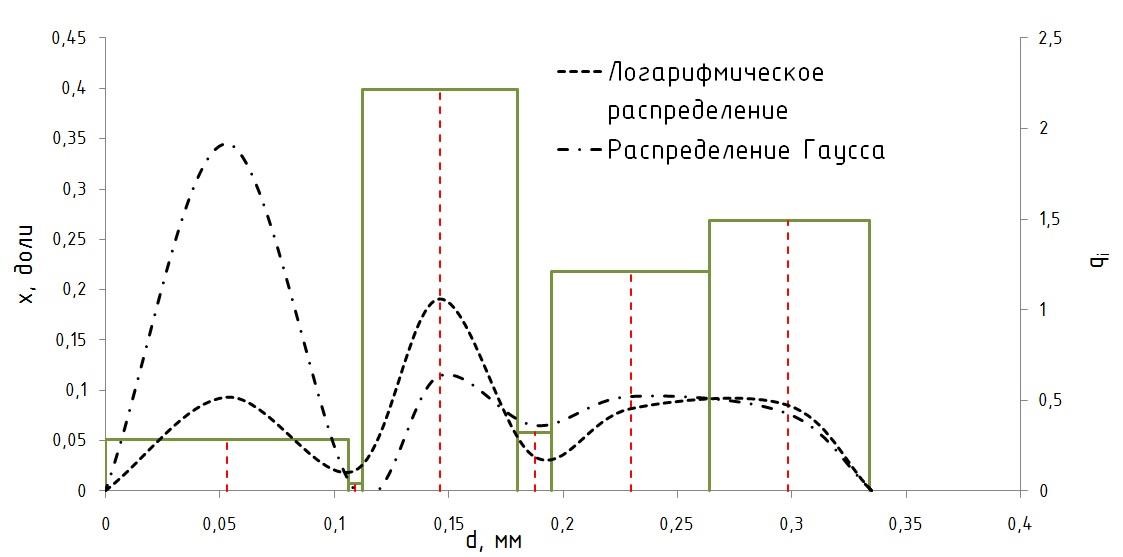 Рис. 2. Гистограмма экспериментального распределения частиц полидисперсного материала в пробе и графики аналитического описания их законом нормального распределения Гаусса и логарифмического нормального распределения. Адекватность математической модели доказывалась по критерию Фишера. Допускаемый разброс значений в трех параллельных опытах составил в среднем 19% для закона логарифмического нормального распределения и 32% - для закона нормального распределения Гаусса. При расчёте значения критерия Фишера уровень значимости выбран 0,05. Стандартное отклонение среднемассового состава q=f(d) для нормального распределения Гаусса в два раза больше, чем для логарифмического нормального распределения [2]. Таким образом, проведенный анализ показал, что при значительном преобладании в пробе мелких частиц (менее 1 мм) для аналитического описания гранулометрического состава полидисперсных материалов целесообразно использовать закон логарифмического нормального распределения. Седиментационный (оптический)Следующий метод  седиментационный (или седиментометрический), который проводится для фракций частиц размером менее 0,05 мм. Разделение таких коллоидно-дисперсных частиц по фракциям основано на различной скорости осаждения частиц разного размера в вязкой жидкости. Его точность во многом определяется точностью метода измерения количества осаждающихся примесей, например, путём измерения общей массы осевших частиц или оценки ослабления луча света после прохождения пробы с примесями. седиментационный (или седиментометрический), который проводится для фракций частиц размером менее 0,05 мм. Разделение таких коллоидно-дисперсных частиц по фракциям основано на различной скорости осаждения частиц разного размера в вязкой жидкости. Его точность во многом определяется точностью метода измерения количества осаждающихся примесей, например, путём измерения общей массы осевших частиц или оценки ослабления луча света после прохождения пробы с примесями.Модель осаждения примесей для прибора седиментационного анализа на основе обработки видеоинформации. Седиментационный анализ своей эффективностью, простотой занимает одно из первых мест среди методов оценки параметров механических примесей в технологических жидкостях. Совершенствование этих методов и разработка эффективных альтернатив повышает точность седиментационного анализа, расширяет сферу его применения и даёт более детальное представление о характере загрязнённости жидкости. Рассмотрим метод измерения количества осаждающихся примесей с использованием анализа видеоизображения процесса седиментации даваемого датчиком видеонаблюдения, в качестве которого может выступать web-kaMepa. На рис. 3 представлена принципиальная схема такого прибора осуществляющего седиментационный анализ с обработкой видеоинформации на ЭВМ. Осаждение механических примесей СОЖ в приборе рис. 3, при условии их начального равномерного распределения по объёму. Из теории обтекания жидкостью твердого тела известно, что сила действия потока жидкости на тело определяется характером обтекания, который математически выражается числом Рейнольдса R. Поток, обтекающий осаждающиеся частицы можно считать ламинарным, соответствующим малым числам Рейнольдса R<10. В таком случае сила сопротивления осаждению частиц со стороны жидкости для шарообразных частиц определяется законом Стокса (3): 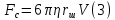 где — 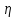 параметр вязкости среды, параметр вязкости среды, 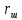 — радиус шара, — радиус шара, 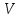 — скорость осаждения. Для расчёта силы сопротивления жидкости для реальных частиц шлама, которые по форме отличаются от идеального шара, вводится седиментационный радиус частиц 1%., который соответствует диаметру сферы, имеющей скорость оседания и плотность частицы шлама. Хотя является обобщённой характеристикой формы частицы, он позволяет достаточно точно описывать распределение частиц по их радиусам, вследствие малого размера, большого количества и случайности формы частиц. — скорость осаждения. Для расчёта силы сопротивления жидкости для реальных частиц шлама, которые по форме отличаются от идеального шара, вводится седиментационный радиус частиц 1%., который соответствует диаметру сферы, имеющей скорость оседания и плотность частицы шлама. Хотя является обобщённой характеристикой формы частицы, он позволяет достаточно точно описывать распределение частиц по их радиусам, вследствие малого размера, большого количества и случайности формы частиц.Как это показано на рис. 3 на частицу в процессе седиментации помимо силы сопротивления осаждению со стороны жидкости, действует ещё сила тяжести и выталкивающая сила Архимеда. 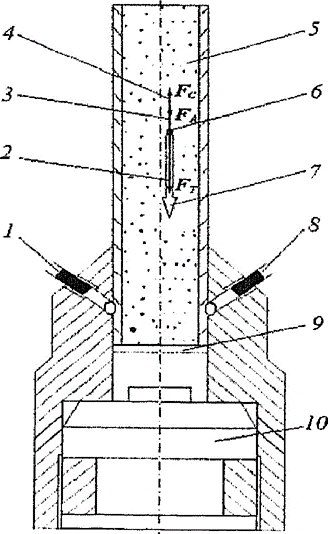 Рис. 3 Схема прибора, осуществляющего седиментационный анализ с использованием ЭВМ. 1,8 — светодиоды; 2,3,4 — соответственно силы тяжести, Архимеда и сопротивления осаждению•, 5 — СОЖ; 6 — частица примесей; 7 — направление осаждения; 9 — стекло; 10 — видеокамера. Сила тяжести для частицы массой 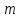 и радиусом и радиусом 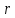 будет (4): будет (4):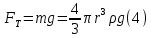 где 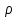 — плотность материала механических примесей, — плотность материала механических примесей, 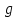 =9,8 м/с ускорение свободного падения. Сила Архимеда для СОЖ с плотностью =9,8 м/с ускорение свободного падения. Сила Архимеда для СОЖ с плотностью 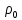 (5): (5):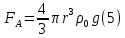 Пропорциональность силы сопротивления движению частиц их скорости осаждения, а также вязкость СОЖ, за пренебрежимо малое время приводят к достижению частицами постоянных скоростей седиментации. Движение частицы с постоянной скоростью, как это следует из законов Ньютона, возможно в случае равновесия силы тяжести, Архимеда и сопротивления (6): 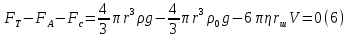 Откуда найдём скорость осаждения частицы 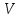 (7): (7):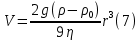 Обозначим 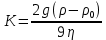 Время необходимое для впадения на дно пробы всех частиц радиусом r равно времени осаждения на дно пробы частицы примеси этого же радиуса к, которая располагалась в начальный момент времени в самой высокой точки пробы на высоте h. Используя введённое обозначение Время необходимое для впадения на дно пробы всех частиц радиусом r равно времени осаждения на дно пробы частицы примеси этого же радиуса к, которая располагалась в начальный момент времени в самой высокой точки пробы на высоте h. Используя введённое обозначение 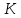 и (7) выразим это время (8): и (7) выразим это время (8):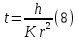 После осаждения всех частиц радиусом r их проекции на дно пробы покроют площадь (9): 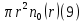 где 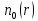 — дифференциальная функция распределения частиц в пробе по их радиусам — дифференциальная функция распределения частиц в пробе по их радиусам 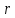 , интегририруемая при , интегририруемая при 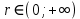 и непрерывная, по крайней мере, при и непрерывная, по крайней мере, при 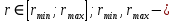 соответственно наименьший и наибольший радиус частиц находящихся в пробе. соответственно наименьший и наибольший радиус частиц находящихся в пробе.Проинтегрировав по переменной 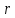 (9) от частиц наименьшего радиуса до частиц наибольшего радиуса найдём площадь, создаваемуо проекциями всех частиц в пробе. (9) от частиц наименьшего радиуса до частиц наибольшего радиуса найдём площадь, создаваемуо проекциями всех частиц в пробе.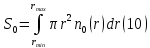 Возьмём из неё площадь проекций частиц, достигающих в ходе осаждения в момент времени 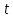 дна пробы. Для этого выделим в пробе СОЖ область, бесконечно близкую к уже осевшим на дно пробы частицам, но не захватывающую их, и представляющую собой элементарный цилиндр высотой дна пробы. Для этого выделим в пробе СОЖ область, бесконечно близкую к уже осевшим на дно пробы частицам, но не захватывающую их, и представляющую собой элементарный цилиндр высотой 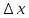 и площадью и площадью 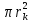 , где , где 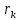 , — радиус трубы, содержащей пробу СОЖ. В этой области располагаются частицы примесей, которые в следующие моменты времени осядут на дно пробы и дадут прирост площади, занимаемой уже осевшими частицами. Количество частиц в указанном элементарном объёме уменьшается со временем, за счёт выпадения частиц в порядке уменьшения их радиусов. Обозначим , — радиус трубы, содержащей пробу СОЖ. В этой области располагаются частицы примесей, которые в следующие моменты времени осядут на дно пробы и дадут прирост площади, занимаемой уже осевшими частицами. Количество частиц в указанном элементарном объёме уменьшается со временем, за счёт выпадения частиц в порядке уменьшения их радиусов. Обозначим 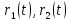 — соответственно минимальный и максимальный радиус частиц, находящихся в области элементарного объёма, тогда общая площадь их проекций на дно пробы будет (11): — соответственно минимальный и максимальный радиус частиц, находящихся в области элементарного объёма, тогда общая площадь их проекций на дно пробы будет (11):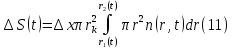 где 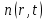 — дифференциальная функция распределения частиц примесей по их радиусам в области указанного элементарного объёма в момент времени — дифференциальная функция распределения частиц примесей по их радиусам в области указанного элементарного объёма в момент времени 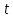 . .Особенностью процесса осаждения, лежащей в основе седиментационного анализа, является различное время осаждения частиц разных радиусов (8). Это позволяет выделить в процессе осаждения три этапа в зависимости от изменения AS( 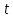 ): ):До момента времени 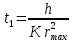 , число частиц , число частиц 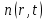 осаждающихся на дно в момент времени осаждающихся на дно в момент времени 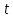 для любого радиуса для любого радиуса 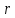 (12): (12):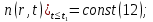 В промежутке времени от 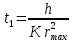 до момента до момента 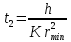 , число частиц , число частиц 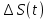 монотонно уменьшается за счёт постепенного выпадения в осадок частиц примесей. Выпадение происходит, начиная с крупных частиц примесей, самых тяжёлых и заканчивая частицами малыми радиусами; монотонно уменьшается за счёт постепенного выпадения в осадок частиц примесей. Выпадение происходит, начиная с крупных частиц примесей, самых тяжёлых и заканчивая частицами малыми радиусами;После момента времени 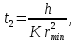 поступление частиц всех радиусов на дно пробы прекращается (13): поступление частиц всех радиусов на дно пробы прекращается (13):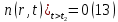 На рис.4 три этапа показаны в их временной последовательности. 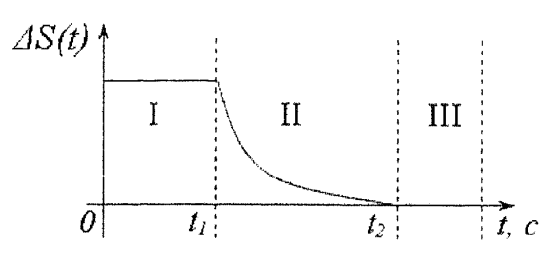 Рис. 4 Показаны три этапа в поступлении на дно пробы частиц примесей. Нужна дифференциальная функция распределения числа частиц 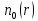 для этапа 2, а затем, найденная зависимость будет справедлива для этапов 1 и 3. Выражение для роста площади с течением времени, которую занимают проекции частиц на дно пробы осевших на него к моменту времени для этапа 2, а затем, найденная зависимость будет справедлива для этапов 1 и 3. Выражение для роста площади с течением времени, которую занимают проекции частиц на дно пробы осевших на него к моменту времени 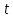 . .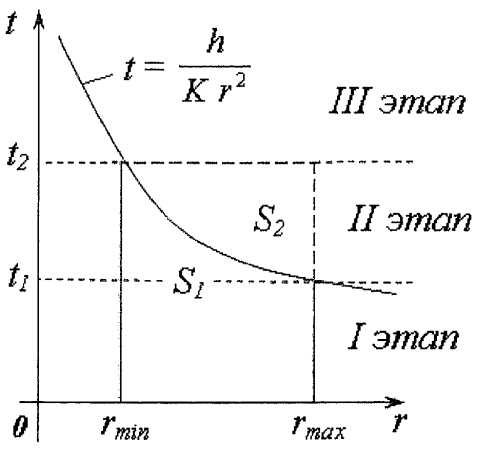 Рис.5 Показана зависимость времени (необходимого на выпадение в осадок групп частиц одинаковых размеров) от радиуса (который имеет осаждающаяся группа частиц). На рис. 5 отображен процесс седиментации в декартовой координатной плоскости, образованной осями времени  и радиусов частиц примесей и радиусов частиц примесей  . В этой плоскости, частицы, осевшие на дно пробы, соответствуют множеству . В этой плоскости, частицы, осевшие на дно пробы, соответствуют множеству 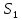 . Множеству . Множеству 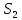 отвечают такие пары отвечают такие пары 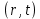 , соответствующие которым группы частиц с радиусом , соответствующие которым группы частиц с радиусом 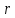 к моменту времени к моменту времени 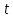 полностью выпали в осадок на дно пробы. Для нахождения общей площади проекций осевших частиц необходимо взять двойной интеграл по области полностью выпали в осадок на дно пробы. Для нахождения общей площади проекций осевших частиц необходимо взять двойной интеграл по области 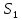 от функции от функции 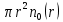 . Для большей наглядности представим . Для большей наглядности представим 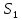 как как 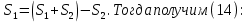 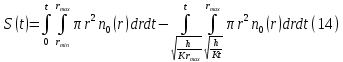 где 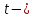 переменная интегрирования. переменная интегрирования.Упростим уменьшаемое в (14), подсчитав интеграл, зависящий от времени, обратив внимание, что подинтеграљное выражение от времени не зависит (15): 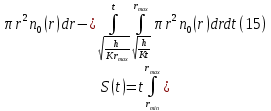 Продифференцируем (15) по времени 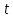 (16): (16):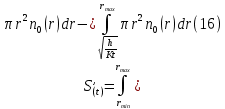 Найдем вторую производную (16) по времени (17): 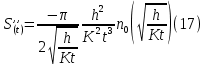 Отсюда можно выразить начальное количество частиц радиуса 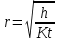 в пробе (18): в пробе (18):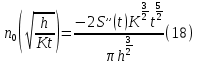 Выражение (18) представляет собой параметрически заданную функцию. Теперь формула (18) верна на этапах 1 и 3. На этапе 3 согласно (13) поступление частиц на дно пробы не происходит и следовательно, 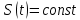 , а , а 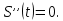 По выражению (18) получим, что число частиц для радиусов соответствующих этому периоду времени тоже будет равно По выражению (18) получим, что число частиц для радиусов соответствующих этому периоду времени тоже будет равно  . В этом случае (16) даёт правильный результат. . В этом случае (16) даёт правильный результат.На этапе 1 рост площади от времени. которую занимают проекции частиц на дно пробы осевших на него к моменту времени 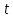 можно представить следующей зависимостью (19): можно представить следующей зависимостью (19):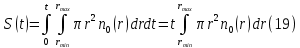 Вторая производная от (19) по времени будет (20): 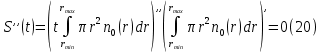 Таким образом, число частиц для радиусов, соответствующих этому периоду времени и в этом случае будет равно согласно (18). Следовательно, на этапах 1 и 3 формула (18) даёт правильный результат, как и на этапе 2. Проверка на адекватность результатов эксперимента Анализ процесса осаждения предварительно равномерно размешанного в СОЖ шлифовального шлама. Параметры шлама, его масса и распределение числа частиц по их радиусам, были определены до его смешивания СОЖ путём разделения его на фракции. Каждая фракция состояла из частиц с радиусами из последовательных диапазонов, что достигалось поочерёдным просеиванием первоначальной смеси части через сита с всё меньшими пропускными размерами решётки. Так как плотность шлама известна, то, зная средний радиус частиц в каждой фракции можно определить и число находящихся в ней частиц. Совокупность данных по всем фракциям даёт приблизительное распределение числа частиц по их радиусам, которое показано на рис. 7 кривой 1. 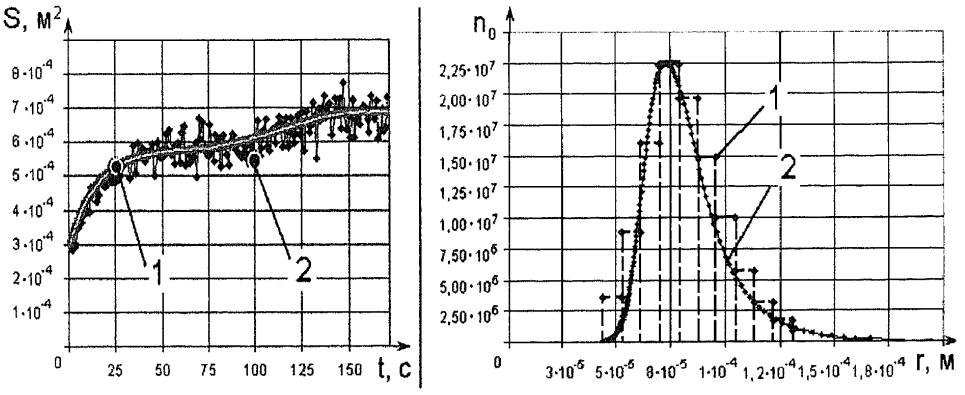 Рис. 6 Обработка информации, поступающей с видеокамеры. Кривая (1) получена аппроксимацией покадровых данных (2) видеокамеры.  Рис. 7 Заданное перед экспериментом (1) и полученное (2) после обработки моделью кривой осаждения (Рис. 6) распределение примесей по их радиусам. Обработав данные с видеокамеры, получили график осаждения примесей (кривая 2, рис.6). Кривая осаждения аппроксимировалась методом наименьших квадратов полиномами Чебышева 5-й степени, используя предварительное логарифмирование значений. В результате было получено распределение примесей (кривая 2, рис.7) [3]. Таким образом, использование видеоизображения осаждения примесей позволяет устанавливать их распределение по радиусам. Седиментационный (весовой)Разделение частиц по фракциям происходит вследствие различия скоростей оседания зерен неодинакового размера в вязкой жидкости. По формуле Стокса скорость осаждения в жидкости частиц сферической формы (21) 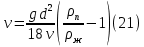 где 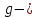 ускорение силы тяжести; ускорение силы тяжести;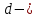 диаметр частиц; диаметр частиц;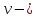 кинематическая вязкость; кинематическая вязкость;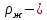 плотность жидкости; плотность жидкости;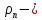 плотность вещества частицы. плотность вещества частицы.Формула (21) справедлива при свободном нестесненном движении зерен; чтобы концентрация частиц не влияла на скорость их осаждения в дисперсной среде, массовое содержание твердой фазы в суспензии не должно превышать 1%. Использование формулы Стокса при седиментационном (гравиметрическим) анализе можно рассмотреть на примере пипеточного метода. Из фракции песка, прошедшего через сито с наименьшими отверстиями, отбирают 10 г песка и перемешивают его с водой в цилиндре емкостью 1 л, помещенном в баню (рис. 8). В цилиндр вставляется пипетка 2, глубина спуска ее кончика 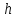 составляет примерно 30 см. составляет примерно 30 см.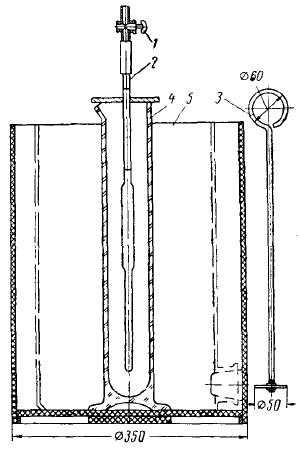 Рис. 8 Седиментометр. 1 -стеклянный кран, 2 – пипетка, 3 – мешалка, 4 – градуированный цилиндр, 5 – стеклянный термостат. Допустим, что необходимо определить в песке количество частиц диаметром меньше 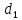 ,. Для этого при помощи формулы (21) вычисляют время ,. Для этого при помощи формулы (21) вычисляют время 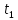 , падения частиц размером , падения частиц размером 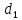 , до глубины спуска пипетки , до глубины спуска пипетки 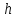 . Очевидно, с глубины . Очевидно, с глубины 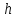 через время через время 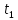 , в пипетку проникнут только те частицы, диаметр которых меньше , в пипетку проникнут только те частицы, диаметр которых меньше 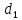 , так как к этому времени после начала их осаждения более крупные зерна расположатся ниже кончика пипетки. Высушив содержимое пипетки, определяют количество находящихся в суспензии частиц диаметром менее или более , так как к этому времени после начала их осаждения более крупные зерна расположатся ниже кончика пипетки. Высушив содержимое пипетки, определяют количество находящихся в суспензии частиц диаметром менее или более 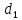 . Это легко сделать, так как масса всей навеси . Это легко сделать, так как масса всей навеси 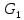 , объем отобранной суспензии , объем отобранной суспензии 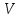 , масса сухого остатка в ней , масса сухого остатка в ней 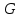 и объем жидкости и объем жидкости 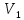 , в цилиндре известны. Очевидно, процентное содержание в породе отобранных пипеткой фракций (т. е. частиц диаметром меньше, чем , в цилиндре известны. Очевидно, процентное содержание в породе отобранных пипеткой фракций (т. е. частиц диаметром меньше, чем 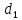 ) будет (22) ) будет (22)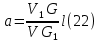 где  процент фракции, прошедший через мелкое сито. процент фракции, прошедший через мелкое сито.Отбирая последующие пробы через другие интервалы времени от начала отстаивания, суспензия точно так же определяют содержание более мелких фракций [1]. Скорость осаждения частиц суспензии монотонно уменьшается с ростом их объемной концентрации за счет повышения эффективной вязкости среды (рис. 9). Для равномерно распределенных в виде кубической решетки монодисперсных сферических частиц объемная концентрация  связана с их диаметром связана с их диаметром 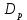 и расстоянием между центрами частиц и расстоянием между центрами частиц 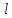 простым соотношением (23) простым соотношением (23)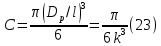 где 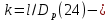 безразмерное расстояние между центрами частиц. безразмерное расстояние между центрами частиц.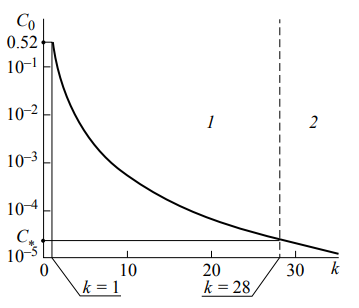 Рис. 9 Зависимость объемной концентрации облака частиц от расстояния между их центрами: 1 – режим частично продуваемого облака; 2 – режим продуваемого облака. На основе анализа ряда приближенных решений стоксовского обтекания частиц и результатов опубликованных экспериментальных данных получены обобщенные критериальные зависимости для коэффициента сопротивления частиц в диапазонах значений числа Рейнольдса 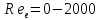 и объемной концентрации и объемной концентрации 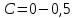 . Число Рейнольдса рассчитывалось по параметрам одиночной частицы с использованием эффективного коэффициента динамической вязкости суспензии . Число Рейнольдса рассчитывалось по параметрам одиночной частицы с использованием эффективного коэффициента динамической вязкости суспензии 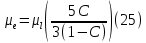 , где , где 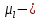 коэффициент динамической вязкости жидкости. коэффициент динамической вязкости жидкости.В отличие от случая нестратифицировнной суспензии, скорость осаждения облака частиц с увеличением их объемной концентрации, как правило, возрастает и превышает скорость осаждения отдельной изолированной частицы. В соответствии с классификацией [5] можно выделить три режима осаждения совокупности частиц (облака): режимы продуваемого, непродуваемого и частично продуваемого облака. В режиме продуваемого облака расстояние между частицами велико, гидродинамическим взаимодействием между частицами можно пренебречь; центр масс облака частиц движется со скоростью одиночной частицы из этого облака. При движении в режиме непродуваемого облака частицы располагаются достаточно близко относительно друг друга – толщина пограничного слоя дисперсионной среды превышает расстояние между частицами. При осаждении системы частиц увлекается вся среда внутри этой системы, и группа частиц движется как единое целое. При этом закономерности движения облака частиц подобны движению равнообъемного шара или тела другой формы. Наряду с поступательным движением облака в нем возникает циркуляция, сохраняющая его форму и размер. Наиболее сложным режимом осаждения является режим частично продуваемого облака (промежуточный режим). В этом случае поток дисперсионной среды частично обтекает систему частиц и частично проходит сквозь нее. При этом возмущения потока за счет взаимодействия с соседними частицами могут вызывать различные вихревые течения, которые будут ускорять или замедлять движение системы частиц. На рис. 10 приведены фотографии движения облака стальных частиц в зависимости от времени для разных размеров частиц, составляющих облако. Из рис. 10 следует, что по мере увеличения числа Стокса продолжительность каждой из стадий гравитационного осаждения совокупности частиц уменьшается, и облако разрушается быстрее. 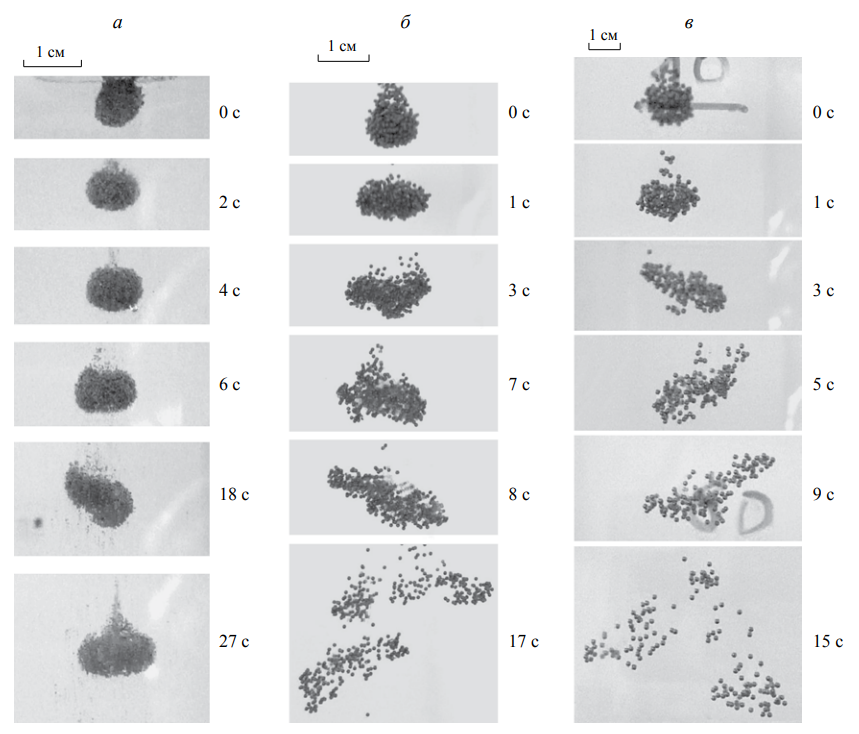 Рис. 10 Фотографии гравитационного осаждения совокупности частиц в глицерине: а – Dp = 0.2 мм, Dc = 6.8 мм, Reс = 0.2, Stk = 0.3; б – Dp = 0.7 мм, Dc= 9.7 мм, Reс = 0.5, Stk = 0.7; в – Dp = 1.3 мм, Dc = 14.4 мм, Reс= 0.8, Stk = 1.1 Проанализированы экспериментальные данные по изменению скорости осаждения системы частиц в зависимости от времени и пройденного расстояния. Обнаружено, что снижение скорости облака частиц в процессе осаждения зависит от начальной концентрации (Рис. 11)[4]. 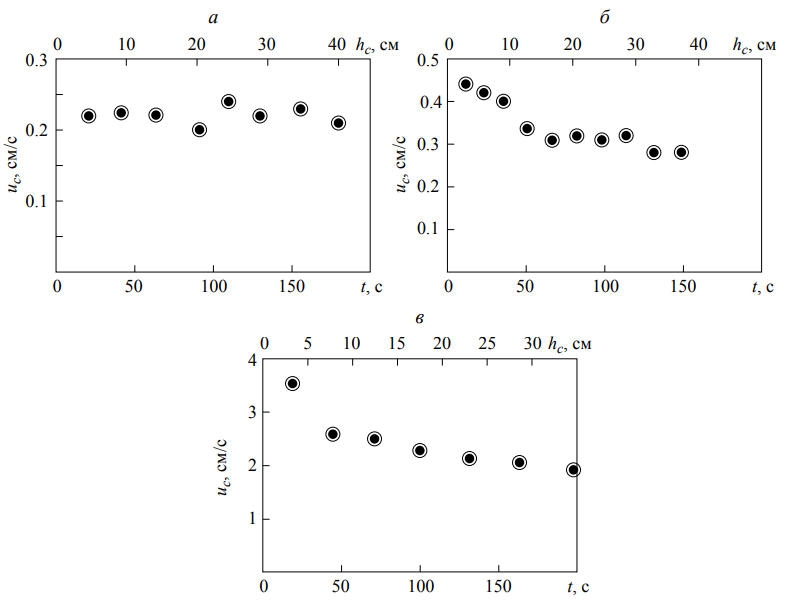 Рис. 11 Зависимость скорости осаждения совокупности частиц от времени и пройденного расстояния (Dp = 0.7 мм): а – C0= 6.8 · 10–4, Dс = 40 мм, Reс = 0.08; б – С0 = 1.3 · 10–3, Dс = 38.6 мм, Reс = 0.12; в– С0= 0.08; Dс = 12.7 мм, Reс = 0.4 Результаты экспериментального исследования процесса гравитационного осаждения консолидированной системы твердых сферических частиц позволяют сделать следующие выводы: Показано, что процесс осаждения облака частиц можно разделить на четыре стадии: стадия движения сфероида, стадия формирования и движения сфероида, стадия деформации сфероида и стадия распада сфероида. Получить обобщенные эмпирические зависимости для коэффициента сопротивления облака частиц от безразмерного комплекса Коэффициент сопротивления облака частиц уменьшается по мере увеличения начальной концентрации совокупности частиц. Следовательно, с увеличением объемной концентрации частиц скорость гравитационного осаждения облака при фиксированном значении числа Рейнольдса увеличивается. Гранулометрический анализ с помощью сканирующего электронного микроскопаНаиболее точным и показательным анализом гранулометрического состава являются более современные методы. Рассмотрим на примере сканирующего электронного микроскопа. Гранулометрический анализ с помощью данного прибора подразумевает оценку образца по изображениям, полученным с электронного микроскопа. На микроскопе можно определить размер частиц с разрешающей способностью при использовании детектора вторичных электронов от 0,003 мкм. Схема работы представлена ниже рис. 12. 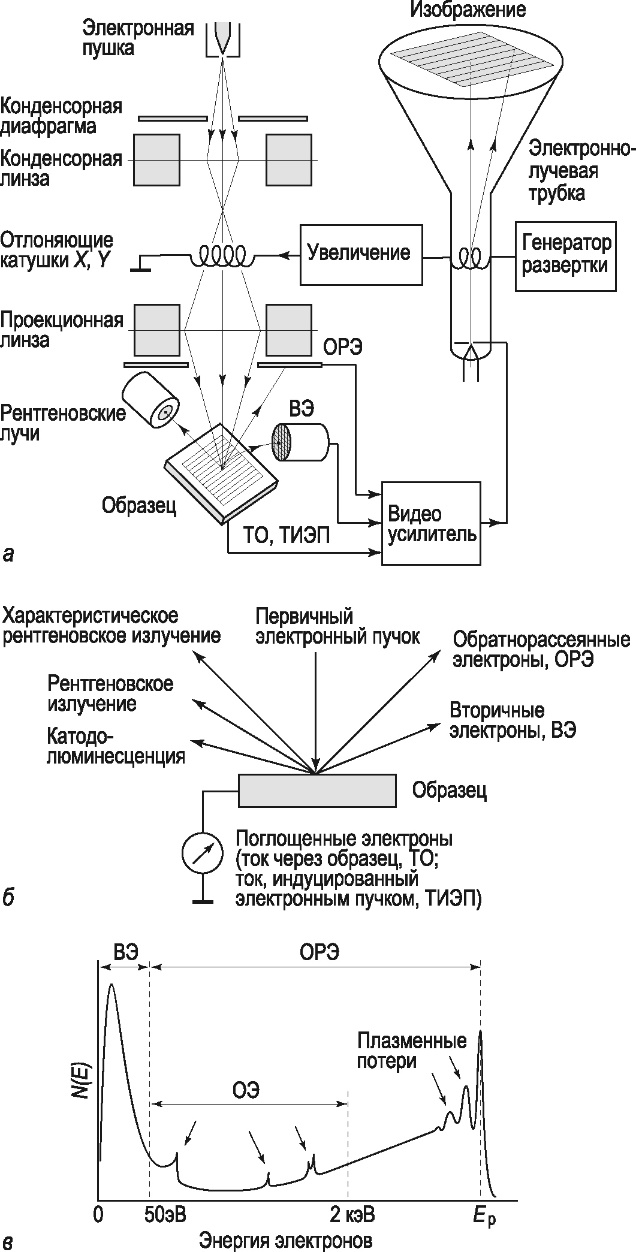 Рис. 12 Принцип работы сканирующего электронного микроскопа. Пучок электронов с первичной энергией около 1-10 кэВ фокусируется системой линз в пятно диаметром 1-10 нм на поверхности исследуемого образца. Сфокусированный пучок сканируется по поверхности с помощью системы отклоняющих катушек синхронно с электронным пучком в видеотрубке, которая используется в качестве оптического дисплея. В сканирующем электронном микроскопе используется детектированные различных сигналов, включая вторичные электроны, обратно рассеянные электроны, рентгеновские излучение и ток через образец. Сканирующий электронный микроскоп позволяет рассматривать детально размеры частиц (рис. 13) (прибор вычисляет за небольшой срок времени их объемное содержание), работать с мельчайшими частицами.   Рис. 13 Фотография образца в масштабе 1:100 мкм В основе метода лазерной дифрактометрии лежит принцип отклонения лазерного луча на разные углы при отражении от частиц разного размера. Затем на основе обработки и анализа интерференционной картины делаются выводы о гранулометрическом составе. К достоинствам лазерной дифрактометрии можно отнести высокую скорость получения результатов, их хорошие сходимость и воспроизводимость. На данный момент этот метод достаточно хорошо автоматизирован В качестве сравнения работы лазерной дифрактометрии и ситового метода можно провести небольшое исследование на примере пылеватого песка (табл. 3). Нетрудно увидеть, что разница в полученных результатах достаточна существенна. Опыт показывает, что чем более мелкими фракциями представлен песок, тем более значительна разница между результатами испытаний указанными методами. Таблица 3– Сравнение гранулометрического состава пылеватого песка, определенного разными методами. 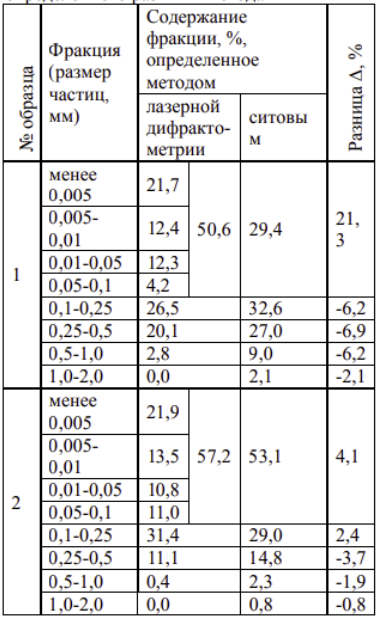 Более простым и менее точным является ситовой метод. Сито - простое по установке, и не является дорогостоящим прибором. Его удобно использовать, где высокая точность не влияет на результат. Современные способы определения гранулометрического состава обладают высокой точностью и позволяют оценивать свойства и обусловленное ими поведение грунта по многим параметрам. ЗаключениеДля определения гранулометрического состава дисперсных материалов используются множество методов, причем обработка результатов измерений проводится с помощью ряда аппроксимационных зависимостей. В данном реферате подробно рассмотрены основные анализы гранулометрического состава: ситовой, седиментационный (оптический), седиментационный (весовой), гранулометрический анализ с помощью сканирующего электронного микроскопа. Каждый из которых, имеет свои преимущества и недостатки. Список использованной литературыГиматудинов Ш.К. Физика нефтяного и газового пласта. - М.: Недра, 1971. Исследования гранулометрического состава полидисперсного продукта методом ситового анализа О.И. Дроздова, А.А. Бобыкин, А.А. Шагарова Издание: XXXII Международная научная конференция «Математические методы в технике и технологиях» - ММТТ-32, 2019, T. 2 ISSN 2587-9049 Модель осаждения примесей для прибора седиментационного анализа на основе обработки видеоинформации, журнал: известия высших учебных заведений. машиностроение Полянсков Ю.В., Евсеев А.Н., Поройков В.А., 2008, 73-80 Архипов В.А., Усанина А.С., Режимы осаждения консолидированной системы твердых сферических частиц, Известия Российской академии наук. Механика жидкости и газа. 2017. № 5. С. 74-85. Фукс Н.А. Механика аэрозолей. М.: Изд-во АН СССР, 1955. 531 с. Измайлова Г.Р., Латифуллин А.Ф. Cравнение традиционных и инновационных методов определения гранулометрического состава породы, В сборнике: Материалы 48-й Всероссийской научно-технической конференции молодых ученых, аспирантов и студентов с международным участием. 2021. С. 217-221. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
