ИРПП. Реферат ИРПП. Реферат по дисциплине "Инженерная реология пищевых продуктов" на тему "

• Название: Реферат по дисциплине "Инженерная реология пищевых продуктов" на тему "
• Дата: 27.06.2022
• Размер: 0.72 Mb.
• Имя файла: Реферат ИРПП.docx
• Тип: Реферат; #617541

Министерство науки и высшего образования РФ

Казанский национальный иследовательский технологический университет

Кафедра Пищевой инженерии

малых предприяти

Реферат

по дисциплине: “Инженерная реология пищевых продуктов”

на тему:

“ Реологические модели простых «идеальных» тел.”

Выполнил:

ст. группы 621-М7

Мухшулов У.Х.

Проверил: д.к.б.н.

Юнусов Э.Ш.

Оглавление

Введение

Основные уравнения напряжений и деформаций «идеальных» тел

Реологические модели сложных реальных тел.

Основные нелинейные эмпирические уравнения напряжений и деформаций для реальных пищевых масс (продуктов)

Применение реологических моделей для описания свойств реальных пищевых масс (продуктов)

Основные структурно-механические свойства пищевых продуктов

Структурно-механические характеристики пищевых продуктов как объективный показатель воздействия

Введение

Реология (от греч. ρέω - теку и λογος - учение) - наука о текучести и деформации сплошных сред (например, обычных вязких жидкостей и жидкостей аномальной вязкости, суспензий и др.)

Термин "реология" ввел американский ученый Юджин Бингам, которому принадлежат важные исследования реологических жидкостей и дисперсных систем. Официально термин "реология" принят на 3-м симпозиуме по пластичности (1929, США), однако, отдельные положения реологии как науки были установлены задолго до этого.

Основные уравнения напряжений и деформаций «идеальных» тел

Для моделирования поведения сложного реологического тела в зависимости от свойств его компонентов в инженерной реологии используются комбинации в различных сочетаниях рассмотренных выше простых идеальных тел, каждое из которых обладает только одним физико-механическим свойством.

Модели простых идеальных тел можно комбинировать, располагая их параллельно, последовательно, смешанно (параллельно и последовательно). В комбинациях число простых элементов может быть разное - два, три, четыре и более, достигая 10-20. Однако практика показывает, что применение в моделях свыше трех, четырех элементов значительно усложняет возможности визуального наблюдения за поведением тел при одновременном изменении такого количества его свойств. Поэтому, чаще всего применяются сложные модели, в которых количество элементов составляет не более трех, четырех.

Для параллельного соединения элементов принимается, что деформация упругого элемента равна деформации вязкого элемента, а суммарное напряжение равно сумме напряжений упругого и вязкого элементов.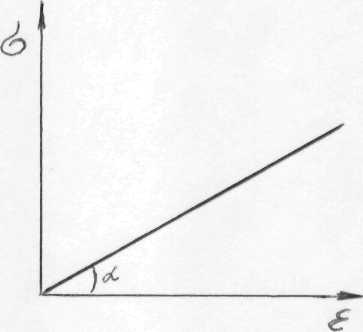




Механическая модель «идеально» упругого тела. Такой моделью представляется упругое тело Гука и изображается в виде пружины (рис. 2.2).

а б

Рис. 2.2. Механическая модель тела Гука

Данная модель характеризуется тем, что при приложении мгновенной нагрузки пружина сжимается, а после снятия возвращается в исходное положение. При этом понимается, что деформации возникают непосредственно после приложения нагрузки и скорость ее распространения практически мгновенна.

Ее поведение описывается законом Гука, основным уравнением которого являются выражения вида:

• 
  при растяжении-сжатии:  ;
  

• 
  при сдвиге:  . (2.11)
  

Зависимость напряжения от деформации (  или  ) принято показывать в виде реограммы т.е. в виде графика (рис. 2.2, б).

Механическая модель «идеально» вязкого тела. Такой моделью представляется вязкое тело Ньютона и изображается в виде цилиндра с жидкостью и поршня с отверстиями (демпфера), через отверстия которого может протекать жидкость (рис. 2.3). При перемещении поршня жидкость через отверстия протекает из одной части цилиндра в другую. При этом перемещение поршня не свободно, а зависит от сопротивления жидкости, т.е. ее вязкости.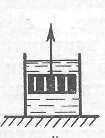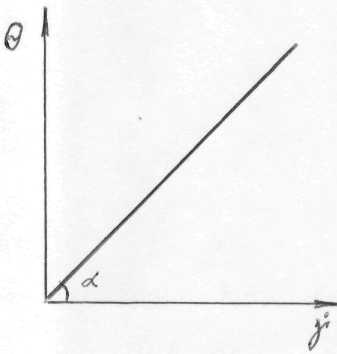




 Поведение модели характеризуется тем, что при приложении мгновенной нагрузки она ведет себя, как абсолютно твердое тело, так как жидкость не способна мгновенно перетечь через отверстия поршня. Если к модели приложить нагрузку и выдерживать под ней или нагрузку прикладывать постепенно, то поршень будет перемещаться в цилиндре в результате протекания жидкости через отверстия. При этом скорость его перемещения зависит от вязкости жидкости, которой он наполнен.

а б

Рис. 2.3 Механическая модель тела Ньютона

Ее поведение описывается законом Ньютона. Основным уравнением, описывающим поведение модели является уравнение вида:

• 
  при продольном смещении:  ,
  

• 
  при сдвиге:  . (2.12)
  

Графическая зависимость 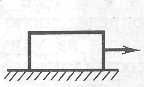 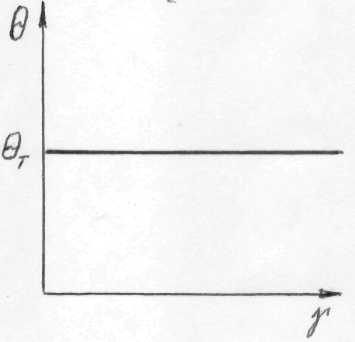 представлена на рис. 2.3 б.




Механическая модель «идеально» пластичного тела. Такой моделью представлено пластичное тело Сен-Венана и изображается в виде пары трения скольжения (рис. 2.4).

а б

Рис. 2.4 Механическая модель тела Сен-Венана

Модель характеризуется тем, что при приложении нагрузки менее критической величины, она остается неподвижной, т.е. никаким изменениям не подвергается. И в случае достижения нагрузки некоторой критической величины происходит смещение одного элемента относительно другого, при этом элемент может перемещаться с любой скоростью.

Ее поведение описывается основным уравнением вида:

, (2.13)

где   - предел текучести материала, т.е. критическая величина напряжения при котором материал начинает течь необратимо, Па.

Графическая зависимость   представлена на рис. 2.4 б.

На практике механические модели «идеальных» тел и их основные уравнения используются для описания поведения, свойств реальных пищевых материалов, жидкостей, которые достаточно близки по свойствам к ним. Однако, в большинстве это невозможно по причине того, что пищевые материалы представляют собой достаточно сложные композиции, которые одновременно могут обладать двумя, тремя и более свойствами.

2.4. Реологические модели сложных реальных тел.

Основные уравнения сложных реологических тел

Основными сложными моделями широко используемыми для моделирования реальных пищевых продуктов, в том числе мясных, являются: модель упруго-вязкого тела (тело Максвелла), модель упруго-вязкого тела (тело Фойгта-Кельвина), модель упруго-пластичного тела, модель вязко-пластич-ного тела (Шведова-Бингама) и др.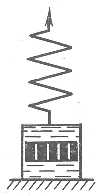

Механическая модель вязко-упругого тела с релаксацией деформаций (тела Максвелла). Механическая модель вязко-упругого релаксирующего тела Максвелла (рис. 2.5) представляет последовательное соединение элементов Гука с модулем упругости   и Ньютона с вязкостью  . На оба элемента действует одинаковое напряжение  . Для последовательного соединения элементов считается, что полная скорость деформации тела равна сумме скоростей ее элементов и каждый элемент передает полную нагрузку.

Рис. 2.5. Механическая модель тела Максвелла

Поведение модели. Если к модели приложить мгновенную нагрузку и сразу снять, то успевает отреагировать только пружина, которая растянется и сожмется, а поршень не успевает сдвинутся. В этом случае модель ведет себя как упругое тело. Если после приложения нагрузки продолжать поддерживать растяжение пружины постоянным, то она релаксирует, т.е. сжимается, перемещая поршень, до тех пор, пока полностью не вернется к своему первоначальному состоянию. В этом случае модель ведет себя, почти как ньютовская жидкость.

Для упругого элемента скорость деформации определяется из закона Гука  , а для вязкого из закона Ньютона  .

Складывая скорости упругой и вязкой деформаций и проведя математические действия, получаем основное реологическое уравнение для тела Максвелла вида:

 или  . (2.14)

Механическая модель вязко-упругого тела с релаксаций напряжений (тела Фойгта-Кельвина). Механическая модель вязко-упругого тела Фойгта- Кельвина (рис. 2.6 ) представляет параллельное соединение элементов Гука с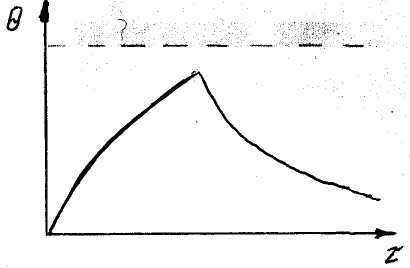




модулем упругости 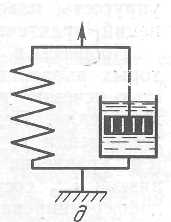  и Ньютона с вязкостью  .

 б

Рис. 2.6 Механическая модель тела Фойгта-Кельвина

Поведение модели. Если к модели приложить нагрузку мгновенно и снять, модель остается неподвижной, т.е. она ведет себя, как абсолютно твердое тело. Если к модели приложить нагрузку и ее удерживать постоянной, то под действием растягивающего усилия пружина удлиняется, и одновременно перемещается поршень в жидкости. При этом движение поршня связано с вязким сопротивлением жидкости, ввиду чего полное растяжение пружины наступает не сразу. После снятия нагрузки, пружина сжимается до первоначальной длины, но это требует времени вследствие вязкого сопротивления жидкости.

Поведение модели описывается основным уравнением Фойгта-Кель-вина вида

. (2.15)

Если предположить, что деформация постоянна, то  =0, при этом наблюдается процесс рассасывания, релаксации напряжений, причем при  =0 напряжение равно какому-то начальному значению  . При интегрировании уравнения в пределах от   до   и времени от 0 до   получают уравнение вида

 или  . (2.16)

Если в этом уравнении выражение   обозначить через  , то уравнение примет вид

, (2.17)

где   - период релаксации, сек.

Данное уравнение называют экспоненциальным уравнением релаксации напряжений.

Период релаксации характеризует быстроту процесса перехода системы из неравновесного термодинамического состояния, вызванного внешним воздействием, в состояние термодинамического равновесия. За этот период напряжение убывает в 2,7 раза.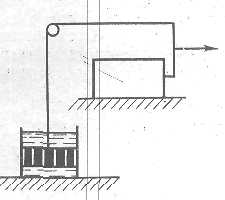




Механическая модель вязко-пластичного тела Шведова-Бингама. Механическая модель (рис. 2.7) представляет параллельное соединение элементов Ньютона с вязкостью   и Сен-Венана с пределом текучести  .

Рис. 2.7 Механическая модель вязко-пластичного тела Шведова-Бингама.

Поведение модели. Если при приложении нагрузки в модели возникают напряжения выражающиеся неравенством 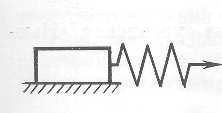 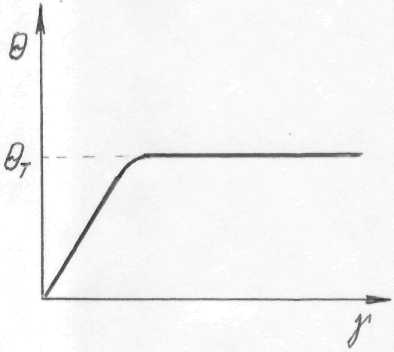, то тело ведет себя как абсолютно твердое недеформируемое. В противоположном случае, когда  , механическая модель описывается основным реологическим уравнением вида:

 или  . (2.18)




Механическая модель упруго-пластичного тела. Механическая модель упруго-пластичного тела (рис. 2.8) представляет последовательное соединение упругого элемента Гука с модулем упругости   и  пластического элемента Сен-Венана с пределом текучести  .

а б

Рис. 2.8. Механическая модель упруго-пластичного тела

Поведение модели. При приложении нагрузки меньше критической величины происходит только растяжение пружины, а пара трения скольжения остается неподвижной, т.е. модель ведет себя, как упругое тело. В случае превышения нагрузки выше критической, происходит перемещение одного элемента пластичного тела относительно другого, при этом пружина остается в том же растянутом состоянии, в котором находилась в момент достижения нагрузки критической величины, т.е. модель ведет себя, как пластичное тело.

При   механическая модель упруго-пластичного тела описывается основным реологическим уравнением Гука имеющего вид  .

При  , механическая модель описывается основным реологическим уравнением Сен-Венана имеющего вид  .

2.5. Основные нелинейные эмпирические уравнения напряжений и деформаций для реальных пищевых масс (продуктов)

В связи с тем, что нередко классические реологические модели не позволяют достаточно точно описать кривую течения материала, в реологии широко используются различные эмпирические и полуэмпирические уравнения, полученные экспериментальным путем. Среди множества уравнений, предлагаемых для описания течения пищевых масс, широко используются два основных уравнения - уравнение Шульмана и уравнение Гершеля-Балкли.

Первое уравнение: уравнение Шульмана, которое имеет вид

= , (2.19)

где а, b - коэффициенты, определяемые экспериментально.

При значениях а = b = 2 это уравнение превращается в уравнение Кэссона, вида

. (2.20)

Второе уравнение: уравнение Гершеля-Балкли, которое имеет вид:

, (2.21)

где   - коэффициент, пропорциональный вязкости при градиенте скорости, равном единице, Па·с^п; п - индекс течения.

Данное уравнение при  =0 приобретает вид степенного уравнения Освальда де Вале

. (2.22)

При п = 1 уравнение приобретает вид уравнения Шведова-Бингама.

Приведенные математические зависимости широко используются для описания поведения пищевых продуктов в различных условиях деформирования при приложении нормальных и касательных напряжений.

2.6. Применение реологических моделей для описания свойств реальных пищевых масс (продуктов)

Представленные выше механические модели широко используются для моделирования и описания свойств реальных пищевых продуктов.

Для моделирования свойств мясных фаршей для вареных колбас рекомендуется механическая модель Шведова-Бингама (см. рис. 2.7). Так, например, при моделирования поведения двух и более приготовленных образцов фаршей, отличающихся хотя бы одним показателем, например вязкостью, наглядно видно, что при приложении нагрузки одной и той же величины, более существенной деформации подвергнется образец, имеющий наименьшую вязкость. А в случае, например, полной потери пластичности материал переходит в состояние вязкого материала, не способного удерживать свою форму, т.е. будет просто растекаться. С помощью данной модели можно исследовать поведение мясных фаршей например, при добавлении воды, различных добавок или оценить механическое воздействие на структуру продукта и т.д.

Для описания поведения цельной мышечной ткани мяса может применяться механическая модель Максвелла. Для описания других материалов могут применяться другие механические модели, рассмотренные выше.

Как показывает практика, применение механических моделей для описания поведения материалов с двумя элементами дают недостаточно точные результаты, которые могут значительно отличаться от результатов, полученных с помощью экспериментальных кривых реограмм. Поэтому с целью повышения точности предлагаются модели, состоящие из трех или четырех элементов простых моделей.

Так, например, для описания поведения материалов, обладающих одновременно упруго-пластично-вязкими свойствами, предлагается механическая модель, состоящая из двух упругих тел, пластичного и вязкого, которая представлена на рис. 2.9 а.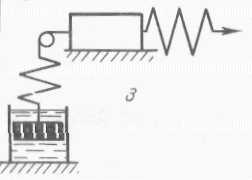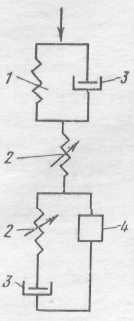

 а б

Рис. 2.9. Механические модели реальных пищевых материалов:

а) - механическая модель продуктов типа мясных фаршей, б) – механическая модель неразрушенной мышечной ткани мяса: 1 - линейно-упругий элемент; 2 - нелинейно-упругий элемент; 3 - вязкий элемент;

4 - элемент, фиксирующий определенное значение деформации.

Данная модель более точно описывает поведение материалов типа мясные фарши, тесто и др., которые обладают одновременно тремя свойствами - упругими, пластичными и вязкими.

Для более точного описания поведения неразрушенной мышечной ткани мяса предлагается механическая модель, представленная на рис. 2.9 б.

Структура неразрушенной мышечной ткани мяса, сложная по своему строению, представлена в виде мышечных волокон, связанных пространственной соединительной пленкой. Все промежутки структуры заполнены тканевой жидкостью: слабо и сильносвязанной влагой. По характеру и прочности связи между частицами мышечную ткань можно отнести частично к конденсационно-кристаллизационным структурам. Подобные структуры обладают рядом свойств твердых тел, но в то же время эластичны, пластичны и т.д., что необходимо учитывать при выборе наиболее целесообразных способов и режимов технологической обработки.

Общая деформация механической модели складывается из нелинейно-упругой с модулем упругости   (последовательно включенный элемент (2), эластичной с модулем упругости   и вязкостью  ₁ (параллельно соединенные элементы (1) и (3)) и пластической с нелинейным модулем упругости  , вязкостью   и фиксатором (последовательно соединенные элементы (2), (3) и параллельно с ними фиксатор - элемент (4).

Данная механическая модель позволяет моделировать деформационные изменения мяса при осевом сжатии. Модель описывается нелинейным дифференциальным реологическим уравнением второго порядка.

Кроме рассмотренных механических моделей, предлагаются и другие для конкретных материалов, познакомиться с которыми можно в специальной литературе.

Тема 3. Основные структурно-механические свойства пищевых продуктов

3.1. Структурно-механические характеристики пищевых продуктов как объективный показатель воздействия. Основные свойства пищевых материалов

3.2. Сдвиговые свойства пищевых материалов

З.3. Компрессионные свойства пищевых материалов

3.4. Поверхностные свойства пищевых материалов

З.5. Влияние технологических факторов на структурно-механические свойства пищевых материалов: температуры, влагосодержания, давления, степени измельчения, продолжительности измельчения и др.

3.1. Структурно-механические характеристики пищевых продуктов как объективный показатель воздействия

Согласно ГОСТу 15.467-79, под качеством продукции понимают совокупность свойств продукции, обуславливающих ее пригодность удовлетворять определенные потребности в соответствии с ее назначением. Наиболее полное представление о качестве продукта дают свойства, определяемые его структурой.

Структура - внутреннее строение продукта и характер взаимодействия между отдельными ее элементами (частицами), которую определяют химический состав, биохимические показатели, температура, дисперсность, агрегатное состояние и ряд технологических факторов.

Для проведения общей оценки качества продукта используется комплекс его свойств: химических, биологических, физических, электрофизических, оптических и др. Среди них комплекс физических свойств, так называемые структурно-механические, предопределяют поведение продуктов в самых разнообразных технологических процессах и энергетических полях. Они являются качественно внешним выражением внутренней сущности объектов, т.е. определяют агрегатное состояние, дисперсность, строение, структуру и вид взаимодействий внутри продукта. В количественном отношении структурно-механические свойства представляют в виде характеристик, т.е. значений, соответствующих физических величин в виде принятых для них единиц измерения. Числовые значения представляют как отношение значения физической величины к единице ее измерения, т.е. безразмерным числам.

Структурно-механические характеристики (СМХ) качественно и количественно определяют поведение продукта в условиях напряженного состояния и позволяют связать между собой напряжения, деформации или скорости деформаций в процессе приложения усилий. Они не являются «чистыми» константами материала и зависят от формы и размеров тела, скорости нагружения, состояния поверхности, воздействия окружающей среды, температуры, структуры и множества других факторов. При известных величинах характеристик можно вычислить значения напряжений и деформаций и в итоге получить необходимые параметры процесса или аппарата, выполнить прочностные и технологические расчеты. То есть, структурно-механические характеристики пищевых материалов выступают как объективный показатель какого-либо воздействия. Кроме того, свойство продукта как объективная реальность позволяет охарактеризовать его качество.

Основные структурно-механические свойства пищевых материалов. Структурно-механические свойства по виду приложения силы (нагрузки, напряжения) к продукту, разделяют на три связанные между собой группы: сдвиговые, компрессионные и поверхностные.

К основным сдвиговым реологическим свойствам материалов относятся -предельное напряжение сдвига   , Па·с, эффективная вязкость  , Па·с, пластическая вязкость  , Па·с, период релаксации  , с.

Они представляют группу свойств, которые наиболее полно отражают внутреннюю сущность материала (объекта) и поэтому их принято считать основными. С их помощью рассчитывают течение материалов в технологических трубопроводах, рабочих органах машин и аппаратов, определяют необходимые усилия для перемещения продукта. Кроме того, они позволяют судить о качестве продукта и степени его обработки, т.е. дают возможность обосновать оптимальные технологические и механические условия процесса, а приборное оснащение позволяет их контролировать и регулировать, обеспечивая постоянное и стабильное качество.

К основным компрессионным (объемным) свойствам материалов относятся: модуль упругости первого рода  , Па; модуль упругости второго рода G, Па, равновесный модуль  , Па; период релаксации деформации при постоянном напряжении  ; с, относительная деформация  ; объемная относительная деформация  ; плотность ρ, кг/м .

Эти характеристики используются для расчета процессов шприцевания, формования, дозирования, транспортирования по трубопроводам и др., а также для оценки качества продуктов.

К основным поверхностным свойствам относятся - адгезия   Па, липкость  , Па, коэффициент внешнего трения  .

Они характеризуют усилие при взаимодействии материалов между поверхностями контакта (адгезию) при нормальном отрыве или сдвиге, которое определяют методом отрыва. При этом, отрыв пищевых материалов друг от друга может быть адгезионным, когезионным и адгезионно-когезионным (смешанным).

Заключение

С проблемами реологии приходится сталкиваться при разработке технологий различных производственных процессов, при проектных работах и ​​конструкторских расчетах для учета поведения различных материалов (особенно при высоких температурах): полимеров, композиционных материалов, бетонов, силикатов, пищевых продуктов и др.

Методы реологии стали применяться для целей оперативного управления технологическими процессами. При этом осуществляется непрерывное или периодическое определение одной или нескольких реологических свойств сырья и (или) продукта по заданной программе и с использованием обратной связи проводится корректировка до заданных пределов параметров сырья, процесса или дозировку входящих ингредиентов.

Методы реологии используют в металлургическом и полимерном производстве, горном деле, при гидравлическом транспортировании и др. отраслях.

Список литературы

1 Рейнер М. реологии. Пер. с англ. М.: Наука, 1965. - 224 с.

2 Шульман 3. П. Беседы о реофизике. Минск: Наука и техника, 1976. - 96с.

3 Виноградов Г. В. реологии полимеров. М.: Химия, 1977. - 440c.