Анализ выживаемости. Реферат по дисциплине Медицинская информатика
 Скачать 334.27 Kb.
|
|
Министерство образования и науки Российской Федерации ФГБОУ ВПО Факультет Кафедра Реферат по дисциплине «Медицинская информатика» «Анализ выживаемости» Выполнил: Принял: Проверил: 2019 г. ОглавлениеВведение. 3 Вычислительные методы 4 Модель для неупорядоченных событий 4 Модели для упорядоченных событий 7 Список использованных источников 11 Введение Данные по многочисленным отказам либо многомерной выживаемости нередко встречаются в биомедицинских и иных анализах. Данные эти появляются в исследовании времени до появления нескольких событий для 1-го объекта, либо времени до появления схожих событий для связанных объектов (к примеру, для членов семьи либо одноклассников). В таких исследованиях критические события коррелированы друг с другом, нарушая требование независимости традиционного анализа выживаемости. Отличают 2 принципиальных варианта: решающие события рассматриваются для одного объекта в конкретном порядке (к примеру, спад болезни) и решающие события различных видов, которые исключается полагать самостоятельными: к примеру, побочные эффекты в одной группе по лечению (treatment). Простой подход к разбору таких данных – изучить время до первого события, пренебрегая другими результаты. Традиционно такой подход неадекватен и приводит к утрате дополнительной информации, поэтому в последнее время становятся популярны 2 подхода: модели с уязвимостью (frailty models) и модели с поправкой на корреляции факторов. В 1-ой модели ассоциация между событиями реализуется как вероятностный момент с известным видом распределения, как правило гамма со средним 1 и неизвестной дисперсией, она не будет рассмотрена. Во 2-ом подходе зависимости между критическими событиями исключены из модели, заместо этого и применяется корреляция оценок. Чаще всего применяются оценки, извлеченные из модели пропорциональных рисков Кокса. Вычислительные методы Пусть  ,  – время события и цензурирования для k-го типа событий и i-го объекта (события и объекты понимаются в обоих смыслах).Введем  и  ,  - вектор регрессионных коэффициентовИнтенсивность будет равна:  ,в первом и:  .во втором случае. Целевые коэффициенты оцениваются методом максимума правдоподобия.Модель для неупорядоченных событий События одного типа Пример В качестве образца смоделируем исследование эффективности фотокоагуляции при лечении диабетической ретинопатии. Сходственные задачи появляются при исследовании семейных болезней. У любого из подопытных из группы риска один случайно отобранный глаз был подвержен фотокоагуляции (воздействию), 2-ой глаз оставлен в контрольной группе. Цель исследования – выявить, что профилактика ощутимо воздействует на болезнь и увеличивает время до утраты зрения. 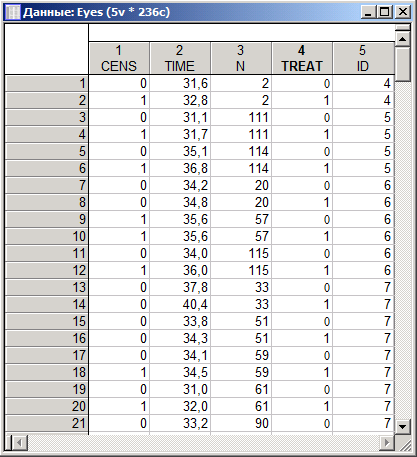 Рисунок 1 – Данные для исследования эффективности фотокоагуляции при лечении диабетической ретинопатии Переменная ID указывает на семью испытуемого, TREAT – на тип глаза («контрольный» или «исследуемый»), N – номер пациента, CENS – индикатор цензурирования. На любого больного в таблице приводится по 2 строки: «проверочный» глаз (TREAT = 0) и «проверяемый» (TREAT = 1); в переменной CENS отмечено случилось ли разрушение сетчатой оболочки глазного яблока к времени окончания обследования, в переменной TIME показано время (в годах), которое клиент был на учете вплоть до наступления мероприятия, N – личный номер больного, ID – личный номер семьи. Задача состоит в том, чтобы представить, что утрата зрения глазом, на который оказано воздействие, начинается позднее, нежели у глаза в отсутствии терапевтического лечения. Воспользуемся регрессионной моделью Кокса с периодами жизни, причинами и цензурированием: 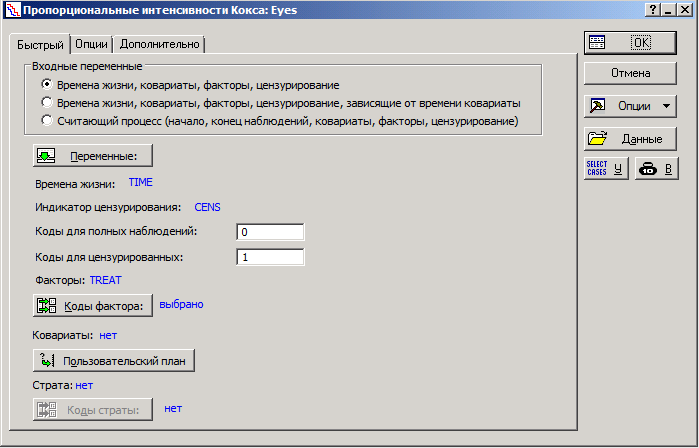 Рисунок 2 – Пропорциональные интенсивности Кокса Переменную ID используем для оценки вариаций и воспользуемся оценкой правдоподобия по Эфрону: 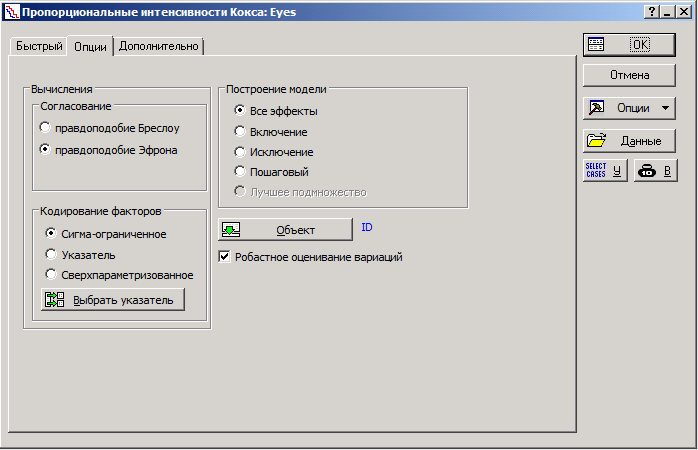 Рисунок 3 – Оценка правдоподобия по Эфрону Графики функции выживаемости выглядят следующим образом (красный – контроль, синий – лечение): 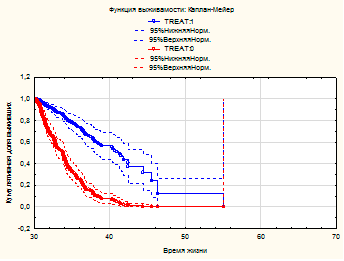 Рисунок 4 – Графики функции выживаемости Модели для упорядоченных событий Для событий, появляющихся только в строго определенном порядке (рекуррентные события) используют другие модели: AG (Андерсена-Гилла) В данной модели для любого объекта обязано быть по одному наблюдению на любое мероприятие либо временной промежуток. В случае если случилось одно мероприятие, то наблюдений обязано быть два: одно для мероприятия и одно для промежутка после данного мероприятия. Схема подразумевает, что базовые функции риска равны для абсолютно всех мероприятий. Пример В этом и последующих примерах будут изучаться результаты лечения псориаза с помощью снятия стресса. 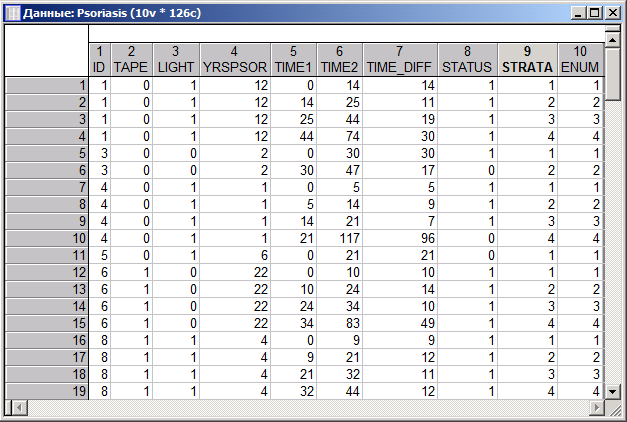 Рисунок 5 – Данные результата лечения псориаза В окне «Регрессионные модели Кокса» выберем «Считающий процесс»:  Рисунок 6 –«Считающий процесс» в окне «Регрессионные модели Кокса» Зададим переменные анализа: 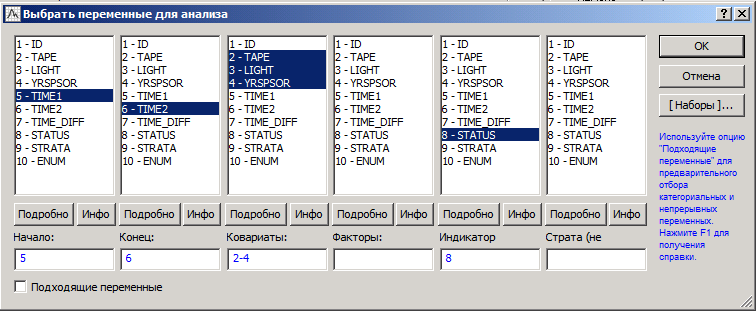 Рисунок 7 – Задание переменных анализа Вариации будут оцениваться по каждому пациенту (переменная ID): 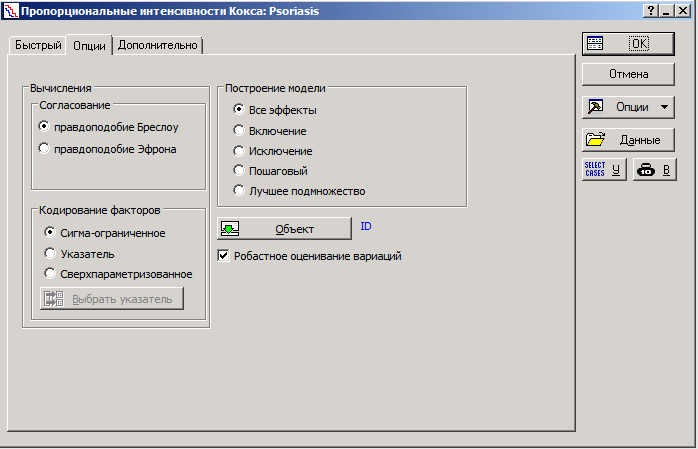 Рисунок 8 – Пропорциональные интенсивности Кокса в анализе лечения псориаза Итоговые оценки параметров в таком случае выглядят следующим образом: 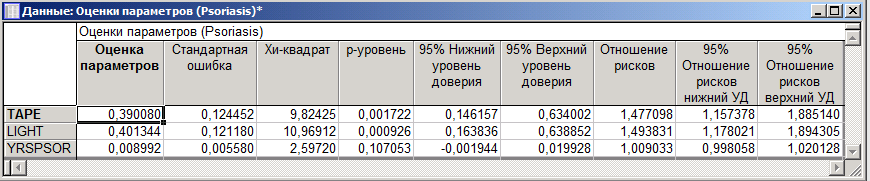 Рисунок 9 – Итоговые оценки параметров Следующие две модели – «условные» (события в них стратифицированы по порядку (первое, второе, ...), для каждой страты – своя базовая функция) PWP-CT (Прентнис, Вильямс и Петерсон, используются номинальные значения времени) 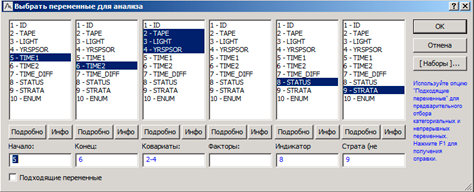 Рисунок 10 – Выбор переменных для анализа Для использования этой модели переключите «Входные переменные» на «Считающий процесс»: Рисунок 11 – Переключение на «Считающий процесс» PWP-GT (Прентнис, Вильямс и Петерсон, используются значения временных интервалов Для использования этой модели переключите «Входные переменные» на «Времена жизни, ковариаты, факторы, цензурирование»:  Рисунок 12 – Переключение на «Времена жизни, ковариаты, факторы, цензурирование» Переменные выбираются аналогично: 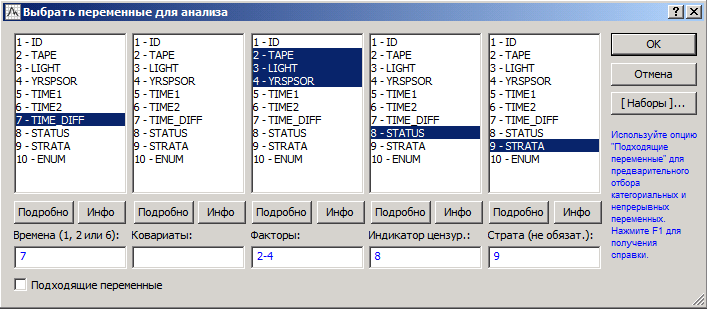 Рисунок 13 – Выбор переменных для анализа WLW (Вей, Лин и Вайсфельд) Схема полагает любое событие единичным процессом и игнорирует связи между распорядком событий – для ее использования нужно располагать данными по любому объекту и событию. В случае если у больного, к примеру, зафиксировано лишь 2 события, а в общей сложности их не более 4, то нужно причислить события 3 и 4, случившиеся в тот же момент, что и событие 2. Список использованных источников Интернет ресурс: «Множественный анализ выживаемости в STATISTICA: модели и примеры в медицинских исследованиях» http://statsoft.ru/solutions/ExamplesBase/branches/detail.php?ELEMENT_ID=942&sphrase_id=77337 |