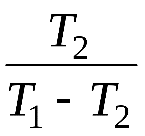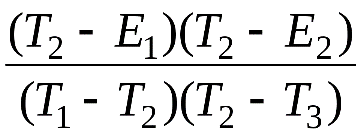Метрологическое обеспечение динамических измерений. реферат. Реферат по дисциплине Метрологическое обеспечение динамических измерений
 Скачать 285 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИСКОЙ ФЕДЕРАЦИИ Федеральное Государственное бюджетное учреждение высшего образования Реферат по дисциплине: Метрологическое обеспечение динамических измерений На тему: 1.Классификация методов обработки динамических характеристик СИ. Метод предварительной оценки и контроля динамических характеристик СИ. 2. Аппроксимация экспериментальной переходной характеристики конечным числом показателей функции. Обучающийся группы: Руководитель: Содержание Введение……………………………………………………………………...........3 1. Классификация методов обработки динамических характеристик СИ.........4 2. Метод предварительной оценки и контроля динамических характеристик СИ…………………………………………………………………………….…….9 3. Аппроксимация экспериментальной переходной характеристики конечным числом показателей функции……………………………………………...……11 Заключение…………………………………………………………………….…20 Список литературы………………………………………………………………21 Введение Метрологическое обеспечение (МО) - это установление и применение научных и организационных основ, технических средств, правил и норм, необходимых для достижения единства и требуемой точности измерений. Научной основой МО является метрология. Организационной основой МО выступает метрологическая служба РФ, состоящая из государственной и ведомственных метрологических служб, базирующихся на основных положениях законодательной метрологии. Нормативно-правовую основу МО составляют комплекс правил, требований и норм, установленных в стандартах и нормативных документах по стандартизации в РФ. Динамическое измерение – это измерение, при котором средства измерений используют в динамическом режиме, т. е. при изменении условий (факторов) за время проведения измерительного эксперимента, которые влияют на результат измерения (оценку измеряемой величины) Цели работы: Описать классификацию методов обработки динамических характеристик СИ. Что является методом предварительной оценки и контроля динамических характеристик СИ. Аппроксимация экспериментальной переходной характеристики конечным числом показателей функции. Классификация методов обработки динамических характеристик СИ Как известно под методом определения динамической характеристики СИ подразумевается совокупность приемов использования средств измерений, средств обработки данных и алгоритмов обработки, позволяющих определить динамическую характеристику исследуемого СИ и оценить точность ее определения. При этом различают прямые и косвенныеметоды определения. Прямой метод определения ДХ СИ реализуется с помощью испытательных сигналов, достаточно близких по форме к характеристическим, причем оценками значений искомой характеристики служат масштабно преобразованные (приведенные) параметры выходного сигнала СИ. Прямым методом можно определить четыре динамические характеристики из числа полных ДХ СИ, по названиям которых даны названия соответствующим методам. 1. Прямой метод определения приведенной переходной характеристикиСИ с помощью ступенчатого испытательного сигнала, при котором искомую характеристику получают путем деления мгновенных значений выходного сигнала на его установившееся значение. 2. Прямой метод определения приведенной импульсной характеристики СИ с помощью импульсного стандартного сигнала, при котором искомую характеристику получают путем деления мгновенных значений выходного сигнала на значение интеграла от него. 3. Прямой метод определения приведенной амплитудно-частотной характеристикиСИ с помощью гармонических стандартных испытательных сигналов, при котором искомую характеристику получают путем деления амплитуд установившихся выходных сигналов на амплитуды соответствующих входных сигналов и статический коэффициент преобразования СИ. 4. Прямой метод определения фазово-частотной характеристики СИ с помощью гармонических стандартных испытательных сигналов, при котором искомую характеристику получают как разность моментов времени, соответствующих испытательных сигналов, умноженную на их круговую частоту. Косвенный метод определения ДХ СИ использует нахождение искомой характеристики на основании известной зависимости между этой характеристикой, испытательным сигналом и откликом на него исследуемого СИ. К косвенному методу относятся структурно-параметрический и параметрический методы определения полной ДХ СИ. Структурно-параметрический метод определения полной ДХ СИ предусматривает нахождение аналитического выражения (структуры) и коэффициентов (параметров) искомой характеристики. Параметрический метод определения полной динамической характеристики СИ направлен на нахождение коэффициентов (параметров) известного аналитического выражения (известной структуры) искомой характеристики. Если использовать приведенные термины и определения применительно к типовым динамическим моделям СИ, (то их структурой является соответствующая передаточная функция, а коэффициентами (параметрами) – их постоянные времени и степень успокоения (для колебательного СИ). На рисунке представлена модель методов определения динамических характеристик СИ, иллюстрирующая связи между отдельными процедурами, приемами и объектами без указаний процессов на детальном уровне. Как видно из рисунка методы определения ДХ СИ делятся на экспериментальные, аналитические и комбинированные – экспериментально-теоретические. Экспериментальные методы реализуются с помощью прямых методов определения ДХ СИ и требуют использования системы или установки для проведения соответствующего эксперимента. 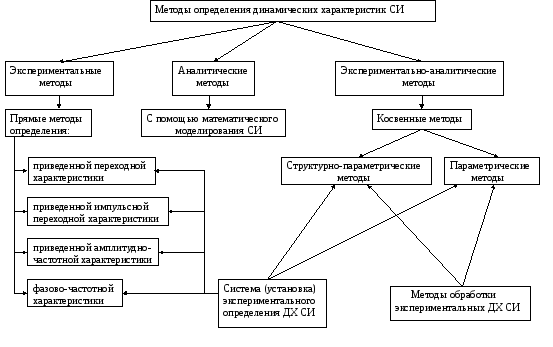 Аналитические методы предусматривают построение или разработку математической модели процессов, происходящих в СИ во время измерения. Как правило, это система дифференциальных уравнений, порядок которой зависит от степени детализации описания процессов, происходящих в СИ. Причем, не следует смешивать математические модели процессов, используемые в аналитических методах определения ДХ СИ, с динамическими моделями СИ, приведенных в таблице. Динамические модели СИ по структуре, наименованию и числу регламентированы ГОСТ 8.508, а математические модели могут быть сколь угодно сложными (сложность ограничена только возможностями исследования их с помощью ЭВМ) и построенными на самых различных принципах. Примерами принципов построения математических моделей являются электротепловое, электрогидравлическое, пневмоэлектрическое и т. п. моделирование. Приведенные принципы моделирования используют так называемый метод аналогий, когда исследуемые явления заменяются изучением аналогичных явлений, так как часто их исследование оказывается проще. Сходство аналогичных явлений заключаются в одинаковом характере протекания всех процессов. Математически аналогичные явления описываются формально одинаковыми дифференциальными уравнениями и условиями однозначности, однако физическое содержание и размерность входящих в них величин различны. Для реализации аналитических методов определения ДХ СИ наличия математических моделей недостаточно. Необходимо также иметь методики исследования этих моделей и алгоритмы получения из них нормируемых ДХ. Преимуществами аналитических методов определения ДХ СИ является относительно малые затраты на получение нормируемых ДХ исследуемого СИ, так как не нужно использовать испытательное оборудование (как правило, дорогостоящего и требующего наличия квалифицированного персонала), и не обязательно иметь реальный образец исследуемого СИ (достаточно чертежа конструкции СИ). Основным недостатками аналитических методов является невысокая точность и достоверность определения ДХ СИ, вызванная невозможностью полного математического описания всех физических процессов, происходящих в исследуемом СИ в процессе его эксплуатации. Поэтому аналитические методы применяются в основном для прогнозирования ДХ средства измерения на этапе его разработки и проектирования и (или) исследования поведения ДХ в зависимости от вносимых конструктивных изменений. От указанных недостатков свободны экспериментально-аналитические методы определения ДХ СИ, которые используют соответствующее испытательное оборудование (систему или установку для экспериментального определения ДХ СИ) и методы (методики) обработки экспериментальных ДХ. Экспериментально-аналитические методы относятся к косвенным методам определения ДХ СИ и являются наиболее широко применяемыми на практике. Метод предварительной оценки и контроля динамических характеристик СИ. Данный метод приведен в ГОСТ 8.508 и относится к структурно-параметрическим методам. В соответствии с данным стандартом устанавливают вид и порядок (т. е. структуру) динамической модели линейных стационарных СИ не выше второго  .Структуру динамической модели СИ определяют с помощью оценки вспомогательных параметров, функционально связанных с коэффициентами полных динамических характеристик. Для оценки вспомогательных параметров с ГИС на вход ИСИ подают кусочно-постоянный испытательный сигнал, изменяющий свои значения через интервал времени  , и считывают выходной сигнал в моменты времени .Для инерционных СИ порядка не выше второго значения выходного сигнала в моменты времени  связаны со значениями этого сигнала в предыдущие моменты времени, а также со значениями входного сигнала через вспомогательные параметры уравнением ,где  - вспомогательные параметры.Вспомогательные параметры оценивают по специальной методике и алгоритму обработки результатов эксперимента и затем используют для установления вида дифференциального уравнения ИСИ в последовательности, приведенной на рисунке. Кроме того, оценивают средние квадратические отклонения вспомогательных параметров, а именно , которые используют при проверке выполнений условий на значения вспомогательных параметров. Например, , если нуль попадает в интервал , и , если единица попадает в интервал .После установления структуры динамической модели ИСИ определяют значения входящих в нее параметров и оценивают точность их определения. Как видно из рисунка, данный метод позволяет определить структуру не всех, а только восьми динамических моделей СИ из пятнадцати, образующих типовые динамические модели. Кроме того, не приводятся расчетные формулы для определения параметров динамических моделей СИ, что создает дополнительные трудности реализации на практике данного метода.  Аппроксимация экспериментальной переходной характеристики конечным числом показателей функции. Данный метод может являться структурно-параметрическим или параметрическим в зависимости от исходных данных и последовательности его реализации. Приведем математическое обоснование метода. Если ставиться задача приближения функции 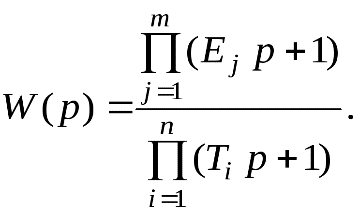 на некотором интервале времени переходного процесса суммой конечного числа экспоненциальных членов, то в случае отсутствия кратных корней передаточная функция ИСИ будет иметь следующий вид Из условий физической реализуемости СИ постоянные времени  и должны быть вещественными и положительными, а порядок числителя выражения не должен превышать порядок знаменателя, т. е. .При этом уравнение переходной функции имеет вид  , где  - весовой коэффициент соответствующей показательной функции.Рассмотрим на конкретных примерах реализацию метода аппроксимации переходной характеристики конечным числом показательных функций. Простейшим случаем является передаточная функция ИСИ второго порядка, т. е. с  =2, для поиска постоянных времени которой производится следующая последовательность действий.1. Вводится вспомогательная функция  .2. Из зарегистрированной переходной характеристики ИСИ выбирают четыре равноотстоящих по времени 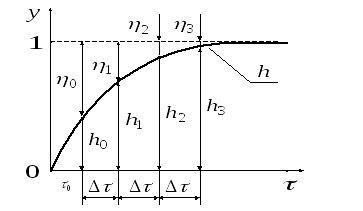 значения и формируют таблицу отсчетов.
3. Решается система из двух уравнение относительно 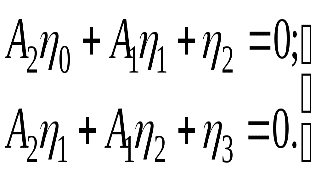 и вида 4. Находятся корни  и квадратного уравнения: Для продолжения вычислений необходимо чтобы корни  были вещественными и положительными, а также удовлетворяли условию 5. Вычисляются постоянные времени по формуле 6. Решается относительно неизвестных  система уравнений вида 7. Находятся весовые коэффициенты переходной функции по формуле  .Задача упрощается, если за время первого отсчета  принять время , тогда величины будут равны искомым весовым коэффициентам.Нахождение значений постоянных времени числителя передаточной функции производится по выражениям, вид которых зависит от значения  .В таблице приведены формулы связи постоянных времени с весовыми коэффициентами для различных значений .
Поскольку числовые значения постоянных времени и весовых коэффициентов уже вычислены соответственно в п. 5 и п. 7, то по данным таблицы определяют значения постоянных времени при заданном значении или путем последовательного перебора значений , если оно не было задано.Из числа типовых динамических моделей СИ передаточной функции при  соответствуют динамические модели (структуры) № 3, № 4, № 5 и № 6.Если структура динамической модели конкретного ИСИ неизвестна, то данный метод реализуется путем последовательного перебора в порядке усложнения указанных моделей и определения значений соответствующих параметров до тех пор, пока фактическая погрешность установленных динамических характеристик станет меньше заданной. В этом случае метод аппроксимации переходной характеристики конечным числом показательных функций будет называться структурно-параметрическим. Если же структура динамической модели ИСИ известна и определяются только значения постоянных времени, то данный метод будет являться параметрическим. При =3 поиск постоянных времени передаточной функции ИСИ по данному методу производится в той же последовательности, что и для =2, однако расчетные формулы имеют несколько более сложный вид. Рассмотрим эту последовательность действий.1. Вводится вспомогательная функция .2. Из зарегистрированной переходной характеристики ИСИ выбирают шесть равноотстоящих по времени значения и формируют таблицу отсчетов.Таблица 4.3
3. Решается система из трех уравнение относительно 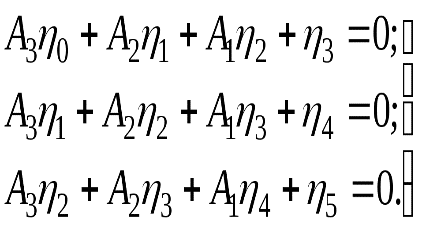, и вида 4. Находятся корни , и кубического уравнения: Для продолжения вычислений необходимо чтобы корни были вещественными и положительными, а также удовлетворяли условию 5. Вычисляются постоянные времени по формуле 6. Решается относительно неизвестных 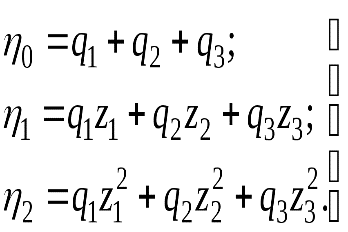система уравнений вида 7. Находятся весовые коэффициенты переходной функции по формуле .Задача упрощается, если за время первого отсчета принять время , тогда величины будут равны искомым весовым коэффициентам.Нахождение значений постоянных времени числителя передаточной функции производится по выражениям, вид которых зависит от значения .В таблице приведены формулы связи постоянных времени с весовыми коэффициентами для различных значений .Как было отмечено выше, типовые динамические модели СИ имеют порядок не выше второго, т. е.  . Однако некоторые СИ должны нормироваться по условиям применения динамическими моделями более сложных порядков. Примерами таких СИ являются датчики температур газовых потоков, используемых при исследованиях, испытаниях и эксплуатации изделий авиационной техники. В соответствии с ОСТ 1 00418 их динамические модели могут иметь порядок до .
Поскольку числовые значения постоянных времени и весовых коэффициентов уже вычислены соответственно в п. 5 и п. 7, то по данным таблицы определяют значения постоянных времени при заданном значении или путем последовательного перебора значений , если оно не было задано.Дальнейшие примеры аппроксимации на большее число понятен. Если необходимо найти постоянных времени передаточной функции ИСИ вида, то необходимо иметь не менее равноотстоящих отсчетов из переходной характеристики, т. е. .Если при вычислениях корни не получились вещественными и положительными, а также не удовлетворяют условию , то дальнейшие вычисления следует прекратить и необходимо произвести следующие процедуры:а) повторить заново расчеты, изменив при этом и (или) ;б) более тщательно произвести отсчеты , возможно они были получены с недопустимо большой погрешностью;в) произвести операции сглаживания или фильтрации помех в экспериментальных данных, из которых составляется таблица отсчетов; г) перейти к другой структуре динамической модели ИСИ. Основным недостаткам данного метода является высокая чувствительность к погрешностям, с которыми определяются отсчеты из переходной характеристики и значения и . Поэтому перед началом применения данного метода необходимо производить процедуры уменьшения погрешностей в отсчетах, особенно при использования метода для больших значений .Вторым недостатком является аппроксимация переходной характеристики переходной функцией вида только на интервале времени от до . Вне данного интервала времени переходного процесса поведение функции относительно переходной характеристики неопределенно.К недостаткам можно также отнести ограниченный класс динамических моделей ИСИ, на который распространяется данный метод. Преимуществами метода являются достаточная простота математических формул и возможность автоматизации процесса определения постоянных времени ИСИ. Область применения данного метода – определение параметров динамически моделей ИСИ при  .Заключение В ходе работы описал классификацию методов обработки динамических характеристик СИ. Дал определение и разьяснение методу предварительной оценки и контроля динамических характеристик СИ. Подробно описал аппроксимацию экспериментальной переходной характеристики конечным числом показателей функции. Список используемой литературы 5 ОСТ 1 00418-81. Метод и средства определения динамических характеристик датчиков температур газовых потоков. Грановский В.А. Динамические измерения: Основы метрологического обеспечения. – Л.: Энергоатомиздат. Ленингр. отд-ние, 1984. Каратаев Р.Н., Гогин В.А. Метрология: Учебное пособие. Казань: Изд-во Казан. гос. техн. ун-та, 2004. МИ 1951-88. Динамические измерения. Термины и определения | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
