критерий пирсона. Критерий Пирсона. Реферат по дисциплине Метрология и средства измерений Тема Критерий Пирсона

• Название: Реферат по дисциплине Метрология и средства измерений Тема Критерий Пирсона
• Анкор: критерий пирсона
• Дата: 19.02.2023
• Размер: 77.32 Kb.
• Имя файла: Критерий Пирсона.docx
• Тип: Реферат; #945131

Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Магнитогорский государственный технический университет им. Г.И.Носова»

(ФГБОУ ВО «МГТУ им. Г. И. Носова»)


Институт энергетики и автоматизированных систем

Кафедра автоматизированных систем управления


РЕФЕРАТ

по дисциплине «Метрология и средства измерений»

Тема: Критерий Пирсона


Выполнил: студент гр. АТСб-20

Бузмаков М.А.

Проверил: старший преподаватель кафедры АСУ

Самарина И.Г.


Магнитогорск, 2022

СОДЕРЖАНИЕ

ВВЕДЕНИЕ 3

1 ОБЩИЕ ПОНЯТИЯ КРИТЕРИЯ СОГЛАСИЯ 4

ЗАКЛЮЧЕНИЕ 8

ВВЕДЕНИЕ

Создание сложных систем, обладающих высокими показателями эффективности и надежности возможны лишь при условии получения исходных данных о параметрах элементов, узлов и частей этих систем. Между тем, надежность закладывается при проектировании, обеспечивается при изготовлении и поддерживается в эксплуатации. На каждом из этапов необходимо оценивать фактическую надежность, для этого требуются экспериментальные данные, которые можно получить при испытаниях на надежность.

Испытания на надежность — это определение показателей надежности объекта на основании непрерывного наблюдения за состоянием его работоспособности в условиях, предписанных методикой испытаний. Они являются обязательным видом испытаний при изготовлении изделий и при приемке их от заводов-изготовителей. Методики проведения таких испытаний регламентируются Государственными и отраслевыми стандартами.

Испытания на надежность могут дать объективную информацию о надежности объекта с учетом влияющих при его работе факторов. Вместе с тем испытания на надежность имеют и отрицательные стороны: они требуют больших затрат времени, средств, а также в процессе испытаний расходуется значительная часть ресурса.

Чтобы испытания на надежность были менее трудоемкими и менее дорогостоящими, применяют специальные приемы:

1) использование таких режимов, которые приводят к ускорению процесса возникновения отказов;

2) прогнозирование отказов по изменению тех или иных параметров объекта;

3) использование предварительной информации о надежности испытуемого изделия, а также принципа накопления информации, полученной из разных источников.

Исходными данными, которые подвергаются обработке, являются время наработки на отказ, время наработки на восстановление и число отказов однотипных элементов. После того, как такой материал собран, его обработка позволяет установить законы распределения показателей надежности: вероятность безотказной работы, интенсивность отказов, среднее время наработки на отказ.

До решения основных задач на основе опытных данных для анализа надежности целесообразно сначала проверить, с помощью статистического критерия согласия, на соответствие выбранного теоретического распределения эмпирическому распределению, построенному на основании проведенных испытаний.

1 ОБЩИЕ ПОНЯТИЯ КРИТЕРИЯ СОГЛАСИЯ

В математической статистике часто выделяют особый раздел, в котором рассматривается проверка гипотез. В теории надежности наиболее часто используются критерии согласия − критерий Пирсона ( 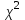) или критерий Колмогорова.

Статистическая гипотеза представляет собой некоторое предположение о законе распределения случайной величины, формулируемое на основе выборки. Она применяется для того, чтобы использовать, полученную при выборке информацию, для суждения о законе распределения случайной величины. Обычно статистическая гипотеза проверяется с помощью критериев согласия, которые позволяют оценить соответствие того или иного теоретического закона распределения некоторому эмпирическому ряду распределения.

Критерием согласия называется случайная величина 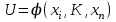(1):
, (1)
где х_i – значение выборки, которая позволяет принять или отклонить гипотезу о предполагаемом законе распределения.

Гипотезу, которая утверждает, что различие между сравниваемыми характеристиками отсутствует, а наблюдаемые отклонения объясняются лишь случайными колебаниями в выборках, то на их основании производится сравнение, которое называют основной гипотезой и обозначают Н₀. Наряду с основной гипотезой рассматривают и альтернативную (конкурирующую, противоречащую) ей гипотезу Н₁. Если нулевая гипотеза будет отвергнута, то будет иметь место альтернативная гипотеза.

Различают простые и сложные гипотезы. Гипотезу называют простой, если она однозначно характеризует параметр распределения случайной величины.

Сложной называют гипотезу, которая состоит из конечного или бесконечного множества простых гипотез.

Проверка гипотезы основывается на вычислении некоторой случайной величины – критерия, точное или приближенное распределение которого известно. Обозначим эту величину через z, ее значение является функцией от элементов выборки z = z(x₁, x₂, …, x_n). Процедура проверки гипотезы предписывает каждому значению критерия одно из двух решений – принять или отвергнуть гипотезу. Тем самым все выборочное пространство и соответственно множество значений критерия делятся на два непересекающихся подмножества S₀ и S₁. Если значение критерия z попадает в область S₀, то гипотеза принимается, а если в область S₁, – гипотеза отклоняется. Множество S₀ называется областью принятия гипотезы или областью допустимых значений, а множество S₁ – областью отклонения гипотезы или критической областью.

Принятие или отклонение гипотезы Н₀ по случайной выборке соответствует истине с некоторой вероятностью, но возможны два рода ошибок. Ошибка первого рода возникает с вероятностью α тогда, когда отвергается верная гипотеза Н₀ и принимается конкурирующая гипотеза Н₁. Ошибка второго рода возникает с вероятностью β в том случае, когда принимается неверная гипотеза Н₀, в то время как справедлива конкурирующая гипотеза Н₁. Доверительная вероятность – это вероятность не совершить ошибку первого рода и принять верную гипотезу Н₀. Вероятность отвергнуть ложную гипотезу Н₀ называется мощностью критерия. Следовательно, при проверке гипотезы возможны четыре варианта исходов, указанных в таблице 1.
Таблица 1 – Проверка гипотез

Гипотеза Н0	Решение	Вероятность	Примечание
Верна	Принимается	1 – α	Доверительная вероятность
	Отвергается	α	Вероятность ошибки первого рода
Неверна	Принимается	β	Вероятность ошибки второго рода
	Отвергается	1 – β	Мощность критерия

Например, когда некоторая несмещенная оценка параметра q вычислена по выборке объема n, то эта оценка будет иметь плотность распределения f(q ), а Т – истинное значение оцениваемого параметра, указанного на рисунке 1.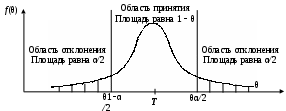


Рисунок 1 - Области и отклонение гипотезы
Если рассматривать гипотезу Н₀ о равенстве q = Т, то чтобы эту гипотезу отвергнуть, надо знать различие между q и Т и насколько оно велико.

Целесообразно полагать одинаковыми значения вероятности выхода параметра θ за нижний и верхний пределы интервала. Такое допущение позволяет минимизировать доверительный интервал, то есть повысить мощность критерия проверки. Суммарная вероятность того, что параметр θ выйдет за пределы интервала с границами θ _{1–α /2} и θ_α/2, составляет величину α. Надо выбрать эту величину настолько малой, чтобы выход ее за пределы интервала был маловероятен. Если оценка параметра попала в заданный интервал, то нет оснований подвергать сомнению проверяемую гипотезу, следовательно, гипотезу равенства q =Т можно принять. Но если после получения выборки окажется, что оценка выходит за установленные пределы, то в этом случае есть основания отвергнуть гипотезу Н₀. Отсюда следует, что вероятность допустить ошибку первого рода равна α (равна уровню значимости критерия).

Если предположить, что истинное значение параметра в действительности равно Т + d, то согласно гипотезе Н₀ о равенстве q =Т – вероятность того, что оценка параметра q попадет в область принятия гипотезы, составит b.

Область принятия гипотезы указана на рисунке 2.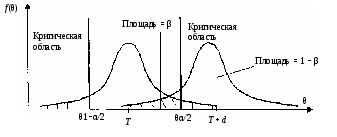


Рисунок 2 - Область принятия гипотезы
Аналогичные рассуждения можно провести для случая, когда истинное значение параметра равно Т – d.

Единственный способ уменьшить эти вероятности, состоит в увеличении объема выборки. При выборе критической области руководствуются правилом Неймана–Пирсона: следует так выбирать критическую область, чтобы вероятность α была мала, если гипотеза верна, и велика в противном случае.

На практике, если P < 0,1, то рекомендуется подыскать другой закон распределения. Рассмотрим применение названных критериев в теории надежности.

2 КРИТЕРИЙ СОГЛАСИЯ ПИРСОНА

Известный английский статистик К. Пирсон в 1900 году предложил для оценки расхождения между эмпирическими и теоретическими частотами критерий, который основан на определении величины хи-квадрат (χ²).

Алгоритм проверки гипотезы при помощи критерия согласия χ²:

1. Построить интервальный статистический ряд вероятностей и гистограмму.

2. По виду гистограммы выдвинуть гипотезу 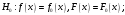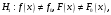(2):
(2)
где f₀(x), F₀(x) – плотность и функция гипотетического закона распределения.

3. Используя метод моментов или максимального правдоподобия, определить оценки неизвестных параметров 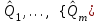гипотетического закона распределения.

4. Вычислить значение критерия по формуле 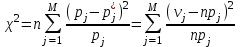(3):
, (3)
где p_j – теоретическая вероятность попадания случайной величины в j-й интервал при условии, что гипотеза H₀ верна 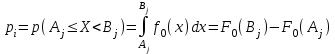(4):

. (4)

После вычисления всех вероятностей p_i проверить, выполняется ли контрольное соотношение .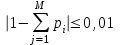

5. Из таблицы χ² (см. приложение 1, табл.1.1) выбирается значение 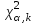, где α − заданный уровень значимости (α = 0,05 или 0,01), а k − число степеней свободы, определяемое по формуле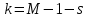 (5):
, (5)
где s – число параметров гипотетического закона распределения.

6. Если 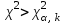, то гипотеза Н₀ отклоняется, в противном случае принимается.

ЗАКЛЮЧЕНИЕ

При исследовании надежности часто воз­никает необходимость идентификации закона распределения вероят­ностей, наибо­лее адекватно описывающего наблюдаемую случайную величину. В этой связи обычно последовательно решают две задачи: сначала оценивают па­раметры закона распределения, выбор которого определяется некото­рыми теоретическими или практическими соображениями, а затем с ис­поль­зова­нием какого-либо критерия (или критериев) согласия проверяется гипотеза о принадлежности наблюдаемой выборки найденному закону. При этом наиболее часто проверка согласия осуществляется по той же самой вы­борке, по которой вычислялись оценки параметров.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. https://skachatvs.com/31419/kriterii-soglasiya-kolmogorova-romanovskogo-pirsona-mizesa-shapiro-i

2. Надежность и эффективность в технике. Справочник в 10 т. (ред. совет: В.С. Авдуевский (пред.) и др. Т.1. Методология. Организация. Терминология) Под ред. А.И. Рембезы. - М.: Машиностроение, 1989. - 224 с.

3. Надежность и эффективность в технике. Справочник в 10 т./Ред. совет: В.С. Авдуевский (пред.) и др. Т.2. Математические методы в теории надежности и эффективности / Под ред. Б.В.Гнеденко. - М.: Машиностроение, 1987. - 280 с.

4. Надежность технических систем. Справочник / Ю.К.Беляев, В.А. Богатырев, В.В. Болотин и др. / Под ред. И.А.Ушакова - М.: Радио и связь, 1985. - 608 с.