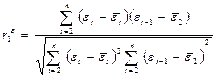АЛГОРИТМЫ ПОСТРОЯНИЕ ЛИНЕЙНЫХ ПО ПАРАМЕТРАМ МОДЕЛЕЙ. Реферат по дисциплине структура и алгоритмы обработки данных алгоритмы построяние линейных по параметрам моделей

• Название: Реферат по дисциплине структура и алгоритмы обработки данных алгоритмы построяние линейных по параметрам моделей
• Дата: 01.04.2022
• Размер: 136.84 Kb.
• Имя файла: АЛГОРИТМЫ ПОСТРОЯНИЕ ЛИНЕЙНЫХ ПО ПАРАМЕТРАМ МОДЕЛЕЙ.docx
• Тип: Реферат; #433664

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ

«МОСКОВСКИЙ ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ»

Кафедра управления и информатики

РЕФЕРАТ ПО ДИСЦИПЛИНЕ
СТРУКТУРА И АЛГОРИТМЫ ОБРАБОТКИ ДАННЫХ
«АЛГОРИТМЫ ПОСТРОЯНИЕ ЛИНЕЙНЫХ ПО ПАРАМЕТРАМ МОДЕЛЕЙ»

Аспирант кафедры УиИ:		Жарков А.П.
Шифр специальности:		05.13.01
Научный руководитель:		д.т.н., проф. Борисов В.В.
Преподаватель:		к. т. н., доц. Виноградова Н.А.

Москва, 2022

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ 3

1.ПОСТАНОВКА ЗАДАЧИ, СОСТАВ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ И ОСНОВНЫЕ МЕТОДЫ, И АЛГОРИТМЫ ЧИСЛЕННОГО ЛИНЕЙНОГО РЕГРЕССИОННОГО АНАЛИЗА 4

2.ПОСЛЕДСТВИЯ НАРУШЕНИЯ ПРЕДПОСЫЛОК РЕГРЕССИОННОГО АНАЛИЗА 6

3.ШАГОВЫЕ АЛГОРИТМЫ ВЫБОРА «НАИЛУЧШЕЙ МОДЕЛИ» 8

4.АНАЛИЗ КАЧЕСТВА МОДЕЛИ: КОЛИЧЕСТВО ПОКАЗАТЕЛЕЙ КАЧЕСТВА ДИСПЕРСНОГО АНАЛИЗА, АНАЛИЗ ОСТАТКОВ 11

ЗАКЛЮЧЕНИЕ 13

СПИСОК ЛИТЕРАТУРЫ 14

ВВЕДЕНИЕ

Цель освоения и написания реферата являеля: привести алгоритмы построения линейных по параметрам моделей.

Задачи:

- провести постановку задач, состав экспериментальных данных и основные методы, и алгоритмы численного линейного регрессионного анализа;

- выявить последствия нарушения предпосылок регрессионного анализа;

- описать шаговые алгоритмы выбора «наилучшей модели»;

- выполнить анализ качества модели: количественные показатели качества, элементы дисперсионного анализа, анализ остатков.

1. ПОСТАНОВКА ЗАДАЧИ, СОСТАВ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ И ОСНОВНЫЕ МЕТОДЫ, И АЛГОРИТМЫ ЧИСЛЕННОГО ЛИНЕЙНОГО РЕГРЕССИОННОГО АНАЛИЗА

Задача рекуррентного, или итеративного, оценивания может быть представлена как задача улучшения старой оценки. Наличие такой оценки означает использование некоторой модели (например, в виде программы для ЦВМ), Входной одной сигнал одновременно подается на объект и модель с настраиваемыми параметрами. Настройка параметров производится с помощью настраивающего устройства, на вход которого поступают выходные сигналы объекта и модели[1].

Основные методы, применяемые для численного линейного регрессивного анализа.

Метод наименьших квадратов (МНК) заключается в том, что сумма квадратов отклонений значений y от полученного уравнения регрессии — минимальное. Уравнение линейной регрессии имеет вид:

y=ax+b

a, b – коэффициенты линейного уравнения регрессии;

x – независимая переменная;

y – зависимая переменная.

Нахождения коэффициентов уравнения линейной регрессии через метод наименьших квадратов: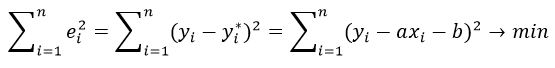



частные производные функции приравниваем к нулю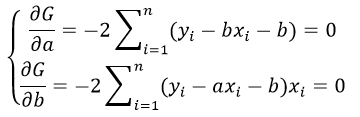



отсюда получаем систему линейных уравнений



Формулы определения коэффициента уравнения линейной регрессии: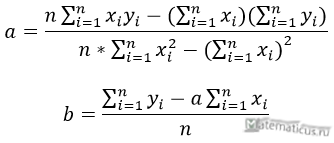



Метод максимального правдоподобия применяется для определения неизвестных коэффициентов модели регрессии и является альтернативой методу наименьших квадратов.

Суть данного метода состоит в максимизации функции правдоподобия или её логарифма. Общий вид функции правдоподобия: где– это геометрическая сумма, означающая перемножение вероятностей по всем возможным случаям внутри скобок.

Общий вид функции правдоподобия: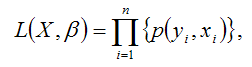

2. ПОСЛЕДСТВИЯ НАРУШЕНИЯ ПРЕДПОСЫЛОК РЕГРЕССИОННОГО АНАЛИЗА

Оптимизационный подход к проблемам управления и принятия решений. Исторически оптимизационные задачи возникли как способы описания и алгоритмизации проблемных ситуаций принятия решений. При этом из множества альтернатив выбора находится одна или несколько, при которых функционал задачи достигает своего максимума или минимума.

Последствия нарушения предпосылок регрессии проявляются в:

• 
  существенной смещенности оценок коэффициентов;
  
• 
  бессмысленности коэффициента корреляции.
  

Дисперсия уровней ряда остатков должна быть одинаковой для всех значений , или, иными словами, на всём протяжении наблюдений (свойство гомоскедастичности). Если это условие не соблюдается, имеет место гетероскедастичность. Гетероскедастичность приводит к тому, что коэффициенты регрессии не являются оценками с минимальной дисперсией, следовательно, они больше не являются наиболее эффективными коэффициентами[1].

Воздействие гетероскедастичности на оценку интервала прогнозирования и проверку гипотезы заключается в том, что хотя коэффициенты и не смещены, дисперсии и, следовательно, стандартные ошибки этих коэффициентов будут смещенными. Если смещение отрицательно, то оценочные стандартные ошибки будут меньше, чем они должны быть, а критерий проверки — больше, чем в реальности. Таким образом, можно прийти к выводу, что коэффициент значим, когда он таковым не является. И наоборот, если смещение положительно, то оценочные ошибки будут больше, чем они должны быть, а критерии проверки — меньше. Значит, возможно ошибочное принятие нулевой гипотезы. Гетероскедастичность подлежит устранению, однако рассмотрение этого вопроса остается за пределами данного пособия.

Для оценки гетероскедастичности при малом объеме выборки можно использовать метод Гольдфельда-Квандта, суть которого заключается в том, что необходимо:

• 
  расположить значения переменной в порядке возрастания;
  
• 
  разделить совокупность упорядоченных наблюдений на 2 группы;
  
• 
  по каждой группе наблюдений построить уравнения регрессии;
  

определить остаточные суммы квадратов для первой и второй групп по формулам:

(28)

рассчитать (в числителе должна быть большая сумма квадратов).

При выполнении гипотезы о гомоскедастичности критерий Fрасч будет удовлетворять F-критерию со степенями свободы для каждой остаточной суммы квадратов (где m – число оцениваемых параметров в уравнении регрессии).

Чем больше величина Fрасч превышает табличное значение F-критерия, тем больше нарушена предпосылка о равенстве дисперсий остаточных величин[2].

3. ШАГОВЫЕ АЛГОРИТМЫ ВЫБОРА «НАИЛУЧШЕЙ МОДЕЛИ»

Частный -критерий, предназначенный для включения фактора в модель, позволяет сравнить прирост факторной дисперсии за счет дополнительно включенного фактора с остаточной дисперсией, приходящейся на одну степень свободы по регрессионной модели в целом,

где , -доля вариации , объясненная регрессией за счет введения фактора ;

- доля остаточной вариации модели, включающей полный набор факторов.

Если числитель и знаменатель формулы умножить на , то получим отношение не долей, а отношение прироста факторной объясняющей суммы квадратов отклонений к остаточной сумме квадратов. Так как прирост факторной суммы квадратов обусловлен включением в модель одного фактора, число степеней свободы для него равно .

Для остаточной суммы квадратов . Фактическое значение частного -критерия сравнивается с табличным при некотором уровне значимости . Если наблюдаемый -критерий превышает табличное значение, то фактор признают значимым и оставляют в модели, если наблюдаемый -критерий меньше табличного, то фактор признается незначимым и принимается гипотеза .

Аналогичную процедуру можно применять и для усложнения модели путем решения вопроса о включении в нее нового фактора. В пакетах прикладных программ, например в пакете STATISTICA, реализованы как процедура включения, так и процедура исключения фактора из модели. Критические значения критериев для включения и исключения факторов и пользователь определяет самостоятельно.

В методе исключения анализ начинается с включения в регрессионную модель всех переменных. Затем для каждой переменной вычисляют частную -статистику и ту переменную, для которой -статистика минимальна, исключают из рассмотрения. Затем строят новую модель по оставшимся переменным и после вычисления частных -статистик вновь удаляют одну из переменных. И так до тех пор, пока не будет достигнуто заранее заданное число переменных в модели или все -статистики не станут больше заданного порога.

В методе включения начинают с построения модели, включающей лишь одну переменную, имеющую наибольший по абсолютной величине парный коэффициент корреляции с переменной выхода. Затем вычисляют частные -статистики для всех оставшихся переменных и включают в модель переменную с наибольшей -статистикой. Это эквивалентно включению переменной, имеющей наибольший частный коэффициент корреляции с переменной выхода. Процесс продолжают до тех пор, пока в модели не наберется определенное число переменных или -статистики не станут меньше заданного порога[3].

Преимуществами шаговых методов являются простота алгоритмов, автоматизация выбора наилучшей модели, быстрота вычислений; недостатком - раздельный анализ переменных (по отдельности переменные могут не являться значимыми, но их совместное использование может улучшить показатели регрессионной модели).

Более сложной процедурой является комбинация методов включения и исключения. Выбирают фиксированные пороговые уровни и и на каждом шаге рассматривают возможности добавить переменную, исключить переменную, заменить одну переменную другой, остановить процесс. На каждом шаге вычисляются -статистики переменных, величина и степень допустимой коррелированности переменных, вошедших в регрессионное уравнение.

Другой способ пошагового отбора факторов состоит в использовании скорректированного коэффициента детерминации, определяемого по формуле

В отличие от обычного коэффициента детерминации , который всегда увеличивается при добавлении новых факторов, скорректированный коэффициент детерминации может уменьшаться при добавлении новых переменных, не оказывающих существенного влияния на выходную переменную . Однако даже увеличение скорректированного коэффициента детерминации не всегда означает, что вводимый в модель фактор значим. Поэтому описанный выше метод шаговой регрессии, основанный на использовании и , предпочтительнее.

4. АНАЛИЗ КАЧЕСТВА МОДЕЛИ: КОЛИЧЕСТВО ПОКАЗАТЕЛЕЙ КАЧЕСТВА ДИСПЕРСНОГО АНАЛИЗА, АНАЛИЗ ОСТАТКОВ

Качество модели оценивается по адекватности и точности на основе анализа остатков регрессии. Анализ остатков позволяет получить представление о том, насколько хорошо подобрана сама модель и насколько правильно выбран метод оценки коэффициентов. Согласно общим предположениям регрессионного анализа, остатки должны «вести себя» как независимые (в действительности почти независимые), одинаково распределенные случайные величины. В классических методах регрессионного анализа предполагается нормальный закон распределения.

Исследование остатков полезно начинать с их графика. Нередко встречаются ситуации, когда остатки содержат тенденцию или подвержены циклическим колебаниям. В этом случае говорят о наличии автокорреляции остатков. Иногда автокорреляция связана с исходными данными и вызвана наличием ошибок измерения результативного признака. В других случаях автокорреляция указывает на наличие какой-то достаточно сильной зависимости, неучтенной в модели. Например, при подборе простой линейной зависимости график остатков может показать необходимость перехода к нелинейной модели или включения в модель периодических компонент.

Существуют два наиболее распространенных метода определения автокорреляции остатков:

1. построения графика зависимости остатков от времени и визуальное определение наличия или отсутствия автокорреляции;

2. использование критерия Дарбина–Уотсона и расчет величины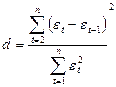



Таким образом, d это отношение суммы квадратов разностей последовательных значений остатков к остаточной сумме квадратов по модели регрессии.

Коэффициент автокорреляции остатков определяется по

Если в остатках существует полная положительная автокорреляция и r1 ε = 1, то d = 0. если в остатках полная отрицательная автокорреляция и r1 ε = -1, то d = 4.

Таким образом, величина d изменяется в переделах:

0£ d £ 4.

Алгоритм выявления автокорреляции остатков на основе критерия Дарбина–Уотсона следующий: выдвигается гипотеза Но об отсутствии автокорреляции остатков; альтернативные гипотезы Н1 и Н1* состоят соответственно в наличии положительной или отрицательной автокорреляции в остатках. Далее по специальным таблицам определяются Критические значения критерия Дарбина-Уотсона dL и du для заданного числа наблюдений n, числа независимых переменных модели k и уровня значимости g. По этим значениям числовой промежуток [0;4] разбивают на пять отрезков. Если фактическое значение критерия Дарбина-Уотсона попадает в зону неопределенности, то нельзя сделать окончательный вывод по этому критерию.

ЗАКЛЮЧЕНИЕ

В реферате были рассмотрены методы и алгоритмы численного линейного регрессионного анализа, приведены примеры формул расчета методов. Метод наименьших квадратов дает наилучшие (в определенном смысле) оценки параметров регрессии.

Выявлены последствия предпосылок регрессионного анализа такие как:

• 
  Существенное смещение оценок коэффициентов;
  
• 
  Бессмысленность коэффициента корреляции.
  

Рассмотрены шаговые алгоритмы выбора «наилучшей модели», так же выделены преимущества и недостатки шаговых алгоритма выбора.

Преимущества:

• 
  Простота алгоритмов
  
• 
  Автоматизация выбора наилучшей модели
  
• 
  Быстрота вычислений
  

Недостатки:

• 
  Раздельный анализ переменных
  

Сделаны выводы о выборе качества модели

СПИСОК ЛИТЕРАТУРЫ

1. Толчеев В.О. Современные методы обработки и анализа данных: Учебное пособие. М.: Издательский дом МЭИ, 2016.

2. Воскобойников Ю.Е. Регрессионный анализ в пакете MATHCAD+CD. − СПб.: Лань, 2021.

3. Теория информационных процессов и систем: учебник для вузов/ Б. Я. Советов и др. – М.: Академия, 2020.