Понятия логики. Реферат по философии. Понятия логики2. Реферат по философии Научный руководитель (личная подпись) (расшифровка)
 Скачать 271.03 Kb. Скачать 271.03 Kb.
|
|
МИНОБРНАУКИ _________________________________________ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Санкт-Петербургский государственный технологический институт (технический университет)» _________________________________________________________ Кафедра философии Бакалавриат Сидоров С.К. Специальность: 15.03.01 ПОНЯТИЯ ЛОГИКИ Реферат по философии Научный руководитель __________________ ________________________ (личная подпись) (расшифровка) Санкт-Петербург 2019 ПОНЯТИЯ ЛОГИКИ Скорее всего, немногие люди задумываются над тем, что они мыслят и рассуждают с помощью понятий. Понятия подобны воздуху: мы их не замечаем, но при этом не можем без них размышлять. Дело в том, что мышление человека отличается от психической деятельности животных, прежде всего тем, что он обладает способностью обобщенно мыслить о предметах, явлениях и процессах окружающего мира в форме понятий. Причем познание реальной действительности реализуется путем образования понятий и оперирования ими. С помощью понятий человек организует свое мышление в обобщенной образной форме. Само мышление при этом является отражением действительности посредством языка. С помощью языка мы можем обобщать предметы некоторого класса или общего вида и мысленнов ыделять их. Результатом таких обобщений являются именно понятия. Например, люди вообще, дома вообще, как понятия и т.д. Выделение осуществляется по определенной совокупности признаков, объединяющих данный класс предметов. Признаки — это то, в чем предметы сходны друг с другом или отличны друг от друга. Признаками являются свойства и отношения. Предметы могут быть тождественными по своим свойствам (например, сахар и мед сладкие), но могут и отличаться ими (мед сладкий, а полынь горькая). Признаком предметов может быть что угодно, имеющее отношение к ним. Любые свойства, черты, состояния предмета, которые характеризуют предмет и выделяют его среди других предметов. Признаками могут быть не только свойства, принадлежащие предмету. Но так же и те свойства, которые у предмета отсутствуют то же могут рассматриваться как объединяющий признак. Например, отсутствие билета у пассажира или оружия у преступника. Бесхозное имущество. Признак отсутствия хозяина. В образовании понятия всегда участвуют три компонента: Словосочетание (знак), Совокупность объектов, которые им обозначаются (значение), Некоторая идея или отличительный признак, связывающий данное слово с подпадающими под него объектами (смысл). Именно этот отличительный признак выступает сердцем понятия, потому что он связывает слово и объекты. В качестве примера можно привести понятие квадрата. «Квадрат» – это термин, отличительный признак – «правильный четырёхугольник, у которого равны все углы и стороны», объекты – множество геометрических фигур, обладающих этим признаком. Из всего множества геометрических фигур этот признак выделяет какую-то группу фигур, потому что они обладают набором каких-то особых признаков. Важно не путать понятие и слово, которым оно обозначается, так как иногда с одним словом могут связываться разные понятия в зависимости от того, что берётся в качестве отличительного признака. («коса» например или слово «классика») ХАРАКТЕРИСТИКИ ПОНЯТИЙ Основными характеристиками понятий является содержание и объем. Содержание понятия – это та совокупность отличительных признаков, на основании которой предметы выделяются из универсума и обобщаются в одну группу. Объём понятия – это совокупность всех предметов, которые обладают данным отличительным признаком. Важно отметить, что объём понятия всегда задаётся относительно некоторого универсума рассмотрения, то есть множества объектов, которые в принципе могут обладать теми или иными отличительными признаками. Универсумом рассмотрения могут быть люди, живые существа, числа, химические соединения, бытовые приборы, науки, пищевые продукты и т.д. Так понятие «слоны» задаётся на универсуме живых существ, понятие «физика» – на универсуме наук, понятие «чётные числа» – на универсуме чисел, понятие «сыр» – на универсуме пищевых продуктов. Содержание и объём понятия ложатся в основу разделения понятий на разные виды. КЛАССИФИКАЦИЯ ПОНЯТИЙ Понятия классифицируют по объему, по типу и по содержанию По объему понятия бывают: Пустые Не пустые В объеме пустых понятий не содержится ни одного элемента. Пример: слово «русалка». Слово такое есть, а соответствующего предмета нет, поскольку персонаж выдуманный. Или «сферический конь в вакууме». Не пустые понятия содержат в своем объеме хотя бы один элемент. Понятие «Картина «Джоконда» Леонардо Да Винчи» - содержит ровно один элемент. По типу понятия подразделяются на Собирательные Несобирательные Конкретные Абстрактные К собирательным понятиям относятся понятия, которые содержат в себе множества объектом. Пример «трудовой коллектив» - собирательное понятие. Несобирательные понятия относятся к единичным объектом и не содержат внутри себя множественности. Например «компьютер», «стол». Конкретными понятиями являются понятия, элементы объема которых можно представить конкретным образом «звезда», «натуральные числа». К абстрактным понятиям относятся те, которые отображают непредставимые характеристики или отношения «твердость», «легкость», «красота». По содержанию понятия бывают: Положительные Отрицательные Относительные Безотносительные Положительные понятия не содержат префикса отрицания, например, «число», а отрицательное понятие такой префикс содержит. Например, «нечетное число», «невероятность», «несвобода». Интересно, что бытовое понимание отрицательного понятия и логическое отрицательное понятие могут не совпадать. Так, например, понятие «преступление», «война», «разруха» и «голод» с бытовой точки зрения являются отрицательными понятиями, а в логике это понятия положительные, потому что не содержат в себе отрицания. Есть так же отрицательные понятия, которые не употребляются без отрицания, например, понятие «ненастье» и «ненависть». Они в логике так же считаются положительными, поскольку без префикса «не» не употребляются. Относительными понятиями являются те, которые содержат внутри себя какие-то отношения. Например парные понятия «покупатель - продавец», «ученик - учитель». Одно понятие без другого не существует, поэтому они относительные. Все остальные независимые понятия являются безотносительными. МЕТОДЫ ОБРАЗОВАНИЯ ПОНЯТИЙ Образование понятий связано с определенными действиями мышления, которые позволяют выделить у предметов определенные существенные признаки и обобщить их в одну группу, озаглавив эту группу каким – либо понятием. Эти методы следующие: Анализ, т.е. мысленное расчленение содержания предмета на составляющие его свойства или признаки. Сравнение, т.е. установление сходства и различия между предметами. Синтез - мысленное соединение признаков, свойств предмета, отражаемых содержанием понятия. Абстрагирование - выделение единства признаков, составляющих содержание понятия, из всей совокупности признаков предметов. Обобщение. Этот метод предполагает связь с абстрагированием (отвлечением) и по сути является единым двусторонним процессом. Допустим, мы имеем понятие «человек»; в результате абстрагирования получаются признаки, такие, как «способный к производству орудий труда», «способный мыслить», а в результате обобщения - общие понятия «животное», «организм». Действие выделения признаков определенного рода есть абстрагирование по отношению к этим выделяемым признакам; оно есть обобщение, если речь идет о более богатой совокупности признаков, которыми обладают различные виды предметов, соответствующие образуемому понятию. ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ БЫВАЮТ
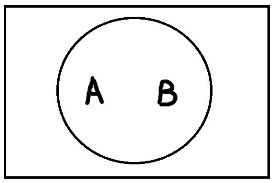
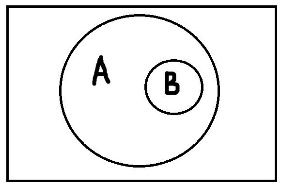
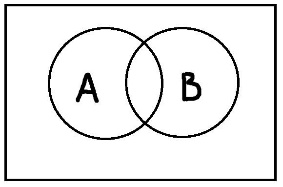
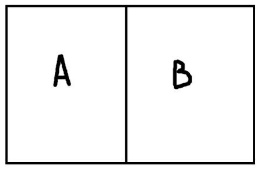
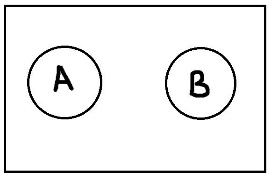
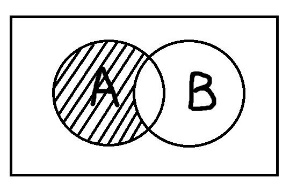
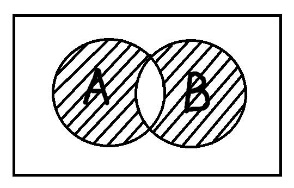
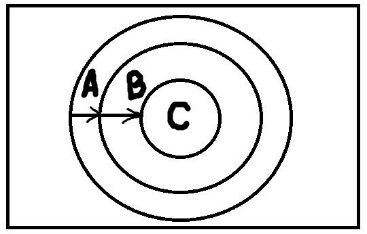
Понятия совместимы, если пересечение их объёмов непусто. Соответственно, если пересечение их объёмов пусто, то понятия несовместимы. Понятие А включается в понятие В, если каждый элемент объёма А также является элементом объёма В. Понятия находятся в отношении исчерпывания, если и только если каждый предмет из универсума рассмотрения является элементом объема либо первого, либо второго понятия. Комбинируя эти основные типы отношений можно получать производные отношения. Равнообъёмность – это отношение, при котором объёмы двух понятий полностью совпадают. Подчинение возникает тогда, когда объём одного понятия полностью входит в объём другого понятия. Пересечение – это отношение, при котором объёмы понятий пересекаются, но полностью не совпадают. Дополнительность – это такое отношение, когда два понятия пересекаются и при этом исчерпывают собой весь универсум рассмотрения. Отношение дополнительности существует, например, между понятиями «температура выше 0°С» и «температура ниже 30°С». Объёмы этих понятий пересекаются, и при этом объём их сложения равен объёму универсума рассмотрения. Противоречие – это отношение, при котором объёмы понятий не пересекаются и исчерпывают весь универсум. Пример «работающие» и «безработные» Соподчинение возникает, когда объёмы понятий не пересекаются, но при этом не исчерпывают собой весь универсум рассмотрения. Видимо здесь речь идет не о подчинении друг другу, а о подчинении обоих понятий какому-то третьему понятию, объем которого вмещает эти два исходных понятия. Например, понятие «животные» включает понятие «рептилии» и «млекопитающиеся». Значит эти два понятия находятся в соподчинении относительно понятия «животные». При этом обратите внимание, что объёмы этих понятий не пересекаются, а объём универсального понятия «животные» содержит множество не подпадающих под А и В элементов.
ЗАКОН ОБРАТНОГО ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ Логики выяснили, что между объёмом и содержанием понятий существует так называемый закон обратного отношения. Суть этого закона состоит в следующем: если первое понятие ýже по объёму, чем второе понятие, то тогда первое понятие богаче второго по содержанию. По большому счёту, этот закон действует, когда мы сталкиваемся с отношением подчинения между понятиями. Например: СПбГТУ –> ВУЗ –> Учебное заведение –> Учреждение образования –> Организация –> Субъект права Понятие «СПбГТУ» шире по содержанию, чем понятие «Субъект права», но уже его по объему. Кроме того, оба понятия находятся в отношениях подчинения. ОПЕРАЦИИ НАД ПОНЯТИЯМИ
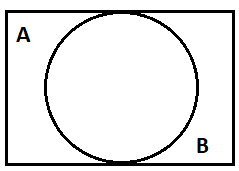
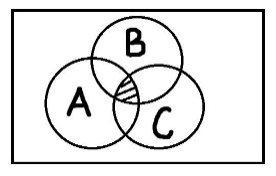
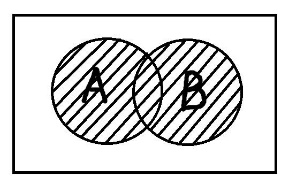
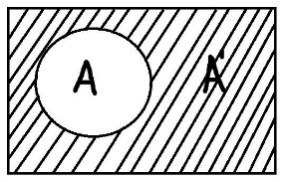
Главная цель операций над понятиями – образование нового понятия, со своим собственным объёмом и содержанием, из имеющихся других или более понятий. Все операции можно разделить на два класса: булевские и не булевские операции. Пересечение понятий – это операция, в ходе которой берутся два или более понятий и как бы накладываются друг на друга. В результате в месте пересечения их объёмов образуется новое понятие, элементами которого будут те предметы, которые одновременно обладают отличительными признаками всех пересечённых понятий. Объединение понятий подобно сложению: мы берём несколько понятий, соединяем их объёмы и тем самым образуем новое понятие, элементами которого будут те предметы, которые обладают хотя бы одним из отличительных признаков объединённых понятий. Вычитание понятий. Берётся несколько понятий и из объёма одного отнимаются объёмы оставшихся. Таким образом, образуется новое понятие, элементами объёма которого будут предметы, обладающие отличительным признаком первого понятия, но не обладающие отличительными признаками тех понятий, которые из него вычитались. Дополнение – это операция, в ходе которой берётся понятие, а затем его объём как бы вычитается из всего универсума рассмотрения. Так создаётся новое понятие, элементами которого будут только те предметы, которые не обладают отличительным признаком изначально взятого понятия. Симметрическая разность – это операция, в некотором смысле обратная пересечению. Нужно точно также взять два или более понятий, наложить их друг на друга, но новое понятие, образованное в результате этого наложения, будет содержать только те элементы, которые обладают не более чем одним отличительным признаком изначальных понятий.
Не булевские операции: Ограничение – это операция, представляющая собой как бы сужение понятия. Ограничить понятие А означает перейти к понятию В, такому что его объём будет строго включаться в объём понятия А. Причём этот переход от А к В представляет собой переход от родового понятия к видовому. Мы можем сузить понятие «химические элементы» до понятия «галогены», а понятие «галогены» до единичного элемента «хлор». При этом старайтесь избежать ошибки подмены операции ограничения понятия операцией анализа. Например, может показаться, что можно сузить понятия «автомобиль» до понятия «колесо». Но это будет неправильно, так как производное понятие при выполнении этой операции должно относиться к тому же классу. То есть, нельзя сказать утверждение, что «все колеса – это автомобили». А вот сузить понятие «автомобили» до понятия «лендроверы зеленого цвета» вполне можно, так как класс этих понятий один и тот же.
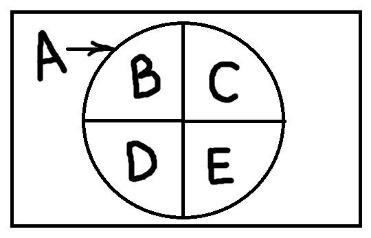
Обобщение – это операция, обратная ограничению. На этот раз мы не сужаем, а расширяем понятие. Обобщить понятие В означает перейти к понятию А, так что объём понятия В будет строго включаться в объём понятия А. Здесь совершается переход от видового понятия к родовому. Деление – это операция, состоящая в том, что берётся понятие, выделяется какая-то характеристика и на основе варьирования этой характеристики исходное понятие делится на несколько частей, в результате чего получается набор новых понятий. Исходное понятие называют делимым понятием. Те понятия, которые образуются после деления – членами деления. Характеристику, на основе которой осуществляется деление – основанием деления. Для иллюстрации предположим, что понятие А – это «месяцы». Основание деления – это принадлежность к времени года. Тогда новообразовавшиеся понятия В, С, D и Е – это «зимние месяцы», «весенние месяцы», «летние месяцы» и «осенние месяцы». Очевидно, что в результате деления может получаться разное количество понятий: всё зависит от делимого понятия и основания деления. При этом следует соблюдать правила деления. Деление должно производиться только по одному основанию. Если использовать наш пример с понятием месяцы, то я не могу разделить его на следующие подпонятия: «зимние месяцы», «весенние месяцы», «летние месяцы», «осенние месяцы» и «мои любимые месяцы». В таком делении используются две характеристики: принадлежность к времени года и моё отношение к конкретному месяцу. Это называется путанным делением и приводит к логическим ошибкам. Члены деления В, С и т.д. должны представлять собой виды по отношению к родовому понятию А. Это то же условие, с которым мы сталкивались при ограничении и обобщении. Нельзя разделить понятие «автомобиль» на понятия «колёса», «двигатель», «руль» и т.п. Опять же нужно задаться вопросом, верно ли утверждение «Все В есть А», «Все С есть А» и так по всем членам деления. Если же вас всё-таки интересуют колёса и двигатель, то необходимо заменить делимое понятие на «части автомобиля», тогда деление станет правильным. Объёмы членов деления не пересекаются, то есть ни один из элементов не может одновременно попадать в В и С или в В и Е и т.д. Члены деления не должны быть пустыми понятиями. Предположим, что исходное понятие А – это «ныне правящие короли». Основание деления – принадлежность к странам. Так вот, среди членов деления не может быть понятий «ныне правящие французские короли» или «ныне правящие немецкие короли», так как это пустые понятия. Если над всеми членами деления B, C, D, E произвести операцию объединения, то мы должны получить объём делимого понятия A. Существует два вида деления: дихотомическое деление и деление по видоизменению основания. Слово «дихотомический» дословно переводится с греческого как «деление надвое». При его осуществлении исходное понятие делится всего лишь на два новых понятия. Выбирается какое-либо основание деления, то есть признак, и в зависимости от наличия или отсутствия этого признака все элементы объёма разделяются на две части. Пусть делимым понятием будет понятие «люди», основанием деления – наличие высшего образования. В таком случае наше исходное понятие будет разделено на два: «люди, имеющее высшее образование» и «люди, не имеющие высшего образования». Второй вид деления – деление по видоизменению основания. В его результате мы можем получить более двух новых понятий. Здесь в качестве основания выбирается какая-либо предметно-функциональная характеристика элементов объёма исходного понятия. Если наше делимое понятие – это «люди», то можно в качестве основания деления взять цвет глаз, цвет волос, национальность и т.п. В результате мы получим набор частично перекрывающихся множеств или понятий, входящих в общее понятие. Эти понятия можно дробить по какому-то признаку еще больше. Такой подход очень удобен для составления каких – либо классификаций. Вершина классификации – исходное делимое понятие – называется корнем. Линии, расходящиеся от неё, подобны веткам. Они ведут к членам деления, от которых в свою очередь также расходятся ветки к новым понятиям. Каждое понятие в классификации называют таксоном. Таксоны группируются по ярусам. Обычно при построении классификаций используются оба вида деления: и дихотомическое, и по видоизменению основания. При этом они могут соседствовать даже в одной классификации, а на каждом ярусе каждый таксон может делиться по своему собственному основанию. ЗАКЛЮЧЕНИЕ Понятия в логике и правильное понимание отношений и операций над ними очень важны, поскольку они играют существенную роль в процессе аргументации и доказательств. Зачастую, многие споры и дискуссии происходят именно из-за неясности, нечеткости и неточности используемых в них понятий. ЛИТЕРАТУРА Канке В.А Философия науки: краткий энциклопедический словарь / М.: Изд. «Омега-Л», 2008. – 328с. Челпанов Г.И. Учебник логики M.: URSS, 2018. - 264с. Кондаков Н. И., Горский Д. П. Логический словарь / М.: Наука, 1971. - 656 с. Демидов И.В. Логика: Учебное пособие для юридических вузов / Под ред. доктора философских наук, проф. Б.И. Каверина. - М.: Юриспруденция, 2000. - 208 с. Гетманова А. Д. Логика: Учебник для студентов высших учебных заведений. – М.: Омега – Л, 2006. – 416 с. |