Оценка периметра многоугольника заданного диаметра. Реферат По теме "Оценка периметра многоугольника заданного диаметра"
 Скачать 1.41 Mb. Скачать 1.41 Mb.
|
|
Глава 2. Оценка периметра пятиугольника единичного диаметра 1. Доказательство равенства четырех диагоналей пятиугольника единице Определение 2.1.1. Диаметром d многоугольника М называется точная верхняя граница расстояний между его точками. [6, 68] d=sup 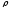 (X,Y) (X,Y)Х  M, У M, У M MТеорема 2.1.1. Диаметр многоугольника равен расстоянию между некоторыми его вершинами. Доказательство. Многоугольник М является ограниченной замкнутой областью. По теореме Вейерштрасса непрерывная функция 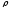 (X,Y) достигает своего максимума в этой области. Иными словами существуют такие две точки А и В многоугольника, что: (X,Y) достигает своего максимума в этой области. Иными словами существуют такие две точки А и В многоугольника, что: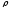 (А, В) = sup (А, В) = sup 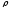 (X, Y) = d. (X, Y) = d.Х  M, У M, У M MОтрезок АВ также будем называть диаметром многоугольника. Ясно, что концы диаметра многоугольника должны находиться на его границе, при этом если хотя бы один из концов диаметра АВ не является вершиной многоугольника, то как видно из рисунка 2.1.1, один из отрезков K1B, K2B будет больше АВ (т.к. один из углов 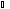 K1АB, K1АB, 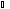 K2АB не является острым), что невозможно. K2АB не является острым), что невозможно.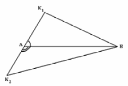 Рис. 2.1.1 Теорема доказана. Итак, диаметр многоугольника совпадает либо с одной из сторон, либо с одной из диагоналей многоугольника. Определение 2.1.2. Выпуклый многоугольник диаметра 1 будем называть оптимальным, если его периметр больше периметра любого другого выпуклого многоугольника диаметра 1. Теорема 2.1.2. Все стороны оптимального пятиугольника меньше 1. Для доказательства теоремы потребуется следующая лемма. Лемма 2.1.1. Сумма расстояний от точки дуги окружности до ее концов принимает наибольшее значение, когда эта точка делит дугу пополам. Доказательство. Пусть Р – точка дуги окружности, точки F и M ее концы (рис. 2.1.2). Из  FPО и FPО и 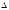 PОM получаем: PОM получаем:FP+PM=2 r sin 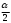 + 2 r sin + 2 r sin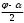 =2 r (sin =2 r (sin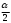 +sin +sin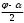 ) = ) ==2 r (2sin 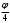 cos cos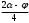 ), ),здесь 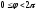 и по симметрии можно считать, что и по симметрии можно считать, что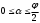 , т.е. , т.е. 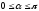 . .Сумма FP+PM принимает наибольшее значение, когда cos 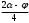 =1. =1.Так как 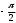 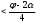 < <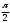 , то , то 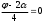 , ,а это значит, что  = = 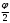 . .Лемма доказана. 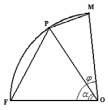 Рис. 2.1.2 Доказательство теоремы. Пусть сторона FT рассматриваемого пятиугольника FPMNT равна 1. Для доказательства проверим, что периметр р пятиугольника FPMNT меньше периметра правильного пятиугольника диаметра 1. Проведем две окружности:  с центром в точке T радиуса FT; с центром в точке T радиуса FT;и  с центром в точке F радиуса FT. с центром в точке F радиуса FT.Очевидно, что остальные вершины пятиугольника будут лежать в области ограниченной окружностями  и и  и в одной полуплоскости относительно стороны FT (в силу выпуклости пятиугольника) (рис. 2.1.3). и в одной полуплоскости относительно стороны FT (в силу выпуклости пятиугольника) (рис. 2.1.3).Возможны два случая расположения вершин P, M, N пятиугольника FPMNT. Рассмотрим первый случай, когда хотя бы одна из прямых РМ и MN пересекает дуги обеих окружностей  , ,  . .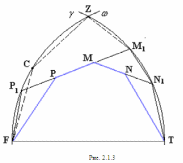 Из рисунка 2.1.3 видно, что периметр p рассматриваемого пятиугольника FPMNT меньше периметра пятиугольника FP1М1N1T, а так же меньше периметра Р1 шестиугольника FСZМ1N1T, где C середина дуги 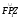 (по лемме 2.1.1). (по лемме 2.1.1).Таким образом, получаем: p< Р1 <4 sin150+1+ 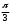  3,0819428. 3,0819428.Рассмотрим второй случай, когда прямые PM, MN пересекают дугу окружности  (рис. 2.1.4). (рис. 2.1.4).Из рисунка 2.1.4 видно, что периметр p рассматриваемого пятиугольника FPMNT меньше периметра P2 пятиугольника FP1М1N1T т.е.: p< P 2 < 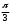 +1+1 +1+1 3,0466. 3,0466.Известно, что периметр P3 правильного пятиугольника равен: P3= 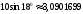 . .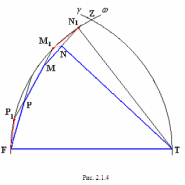 Таким образом, получаем, что периметр рассматриваемого пятиугольника FPMNT меньше периметра правильного пятиугольника диаметра 1. Теорема доказана. Теорема 2.1.3. В оптимальном пятиугольнике, по крайней мере, три диагонали равны 1. Доказательство. Пусть диагональ PT=1 (по теореме 2.1.2). Проведем две окружности:  (T, PT=1) и (T, PT=1) и  (P, PT=1) (рис. 2.1.5). Ясно, что все остальные вершины пятиугольника будут являться внутренними или граничными точками области ограниченной окружностями (P, PT=1) (рис. 2.1.5). Ясно, что все остальные вершины пятиугольника будут являться внутренними или граничными точками области ограниченной окружностями  , ,  и прямой РТ. Причем все три вершины не могут лежать по одну сторону от PT, т.к. PT это диагональ выпуклого пятиугольника (рис. 2.1.5). и прямой РТ. Причем все три вершины не могут лежать по одну сторону от PT, т.к. PT это диагональ выпуклого пятиугольника (рис. 2.1.5).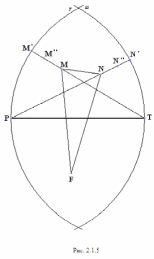 Рассмотрим первый случай, когда прямая MN пересекает дуги обеих окружностей  и и (рис. 2.1.5). (рис. 2.1.5).Допустим, что диагональ FM<1 и точка М отлична от точки M’, тогда сместив точку М в близкую точку М’’ вдоль прямой ТМ’, получим пятиугольник большего периметра, т.е. пятиугольник FPMNT не является оптимальным. Можно поэтому считать, что у оптимального пятиугольника хотя бы одна из диагоналей FM, ТM’ равна 1. Аналогично, хотя бы одна из диагоналей FN, PN’ равна 1. Точно так же рассматривается второй случай, когда прямая MN пересекает только одну из окружностей  , ,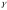 (рис. 2.1.6). (рис. 2.1.6).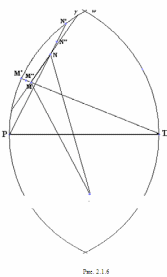 Теорема доказана. Теорема 2.1.4. В оптимальном пятиугольнике, по крайней мере, четыре диагонали равны 1. Доказательство. В силу теоремы 2.1.3 рассмотрим пятиугольник MNTFP у которого три диагонали равны единице, при этом возможны два случая: 1) TP= MF=NF=1; 2) TP= MT=NP=1 (рис. 2.1.7). Рассмотрим первый случай. Проведем три окружности: окружность 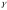 с центром в точке N и радиуса NF=1; с центром в точке N и радиуса NF=1;окружность  с центром в точке M и радиуса MF=1; с центром в точке M и радиуса MF=1;окружность  с центром в точке F и радиуса FM=FN=1. с центром в точке F и радиуса FM=FN=1.Обозначим точки пересечения окружностей  и и  через L, а окружностей через L, а окружностей  и и 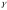 через K (рис. 2.1.7). через K (рис. 2.1.7).Ясно, что вершины P и T пятиугольника с одной стороны будут лежать вне треугольника  MNF, т.к. пятиугольник выпуклый, а с другой стороны должны лежать в области ограниченной окружностями MNF, т.к. пятиугольник выпуклый, а с другой стороны должны лежать в области ограниченной окружностями 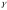 , ,  и и  (область закрашенная на рисунке 2.1.7), т.к. в противном случае, например, если точка Т будет лежать вне этой области, то диагональ МТ >1, а это невозможно т.к. диаметр пятиугольника равен 1. При этом точка P не может лежать на дуге (область закрашенная на рисунке 2.1.7), т.к. в противном случае, например, если точка Т будет лежать вне этой области, то диагональ МТ >1, а это невозможно т.к. диаметр пятиугольника равен 1. При этом точка P не может лежать на дуге 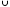 MK , а точка Т не может лежать на дуге MK , а точка Т не может лежать на дуге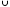 NL, так как в противном случае мы получим, что сторона пятиугольника равна 1, что невозможно по теореме 2.1.2. NL, так как в противном случае мы получим, что сторона пятиугольника равна 1, что невозможно по теореме 2.1.2.Допустим от противного, что NP<1 и MT<1. Проведем два эллипса: l1 с фокусамиM, F , проходящий через точку P; l2 с фокусами N, F , проходящий через точку T. Возможны два случая: а) касательные m 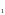 в точке P и m в точке P и m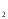 в точке T к эллипсам l1 иl2 соответственно перпендикулярны отрезку PT (рис. 2.1.7). в точке T к эллипсам l1 иl2 соответственно перпендикулярны отрезку PT (рис. 2.1.7).Подвинем отрезок PТ параллельно самому себе на небольшое расстояние, так, что бы новый отрезок P’Т’ (P’  m m , Т’ , Т’ m m ) остался в закрашенной области (или на границе) (рис. 2.1.7). ) остался в закрашенной области (или на границе) (рис. 2.1.7).В результате, длина отрезка PТ не изменится, а длина диагоналей NP’и MT’ не станет больше 1. При этом периметр пятиугольника MP’FT’N больше периметра исходного пятиугольника MPFTN. 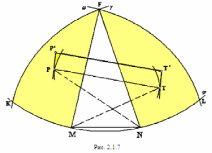 Значит, пятиугольник MPFTN не может быть оптимальным. б) Одна из касательных m  в точке P или m в точке P или m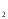 в точке T к эллипсам l1 иl2 соответственно не перпендикулярна отрезку PT. в точке T к эллипсам l1 иl2 соответственно не перпендикулярна отрезку PT.Допустим, что касательная m 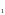 в точке P к эллипсу l1 не перпендикулярна отрезку PT. Проведем окружность в точке P к эллипсу l1 не перпендикулярна отрезку PT. Проведем окружность 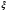 с центром в точке T и радиусом PT=1 (рис. 2.1.8). с центром в точке T и радиусом PT=1 (рис. 2.1.8).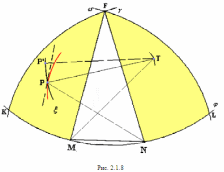 Подвинем точку P по дуге окружности  , которая "выходит" из эллипса l1 и получим точку P’. При этом длина PT не изменится, а точку P мы подвинем на такое расстояние, что бы точка P’ лежала в закрашенной области. А это значит, что диагональ NP’ не станет больше 1. Периметр полученного таким образом пятиугольника MP’FTN больше периметра исходного пятиугольника MPFTN. , которая "выходит" из эллипса l1 и получим точку P’. При этом длина PT не изменится, а точку P мы подвинем на такое расстояние, что бы точка P’ лежала в закрашенной области. А это значит, что диагональ NP’ не станет больше 1. Периметр полученного таким образом пятиугольника MP’FTN больше периметра исходного пятиугольника MPFTN.Значит, пятиугольник MPFTN не может быть оптимальным. Таким образом, в оптимальном пятиугольнике, покрасней мере одна из диагоналей NP, MT равна единице. Теперь рассмотрим второй случай. 2) TP= MT= NP=1 (рис. 2.1.9). Заметим, что вершина F лежит внутри области ограниченной отрезком РТ и дугами  PS и PS и  ST. ST.Предположив, что NF<1 и MF<1 и заменив точку F близкой точкой F’ (см. рис. 2.1.9), мы получим, что РF+FТ 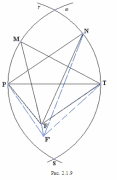 Значит, пятиугольник MPFTN не может быть оптимальным. Таким образом, в оптимальном пятиугольнике, покрасней мере одна из диагоналей NF, MF равна единице. Теорема доказана. 2. Отыскание оптимального пятиугольника Теорема 2.2.1. Оптимальным пятиугольником является правильный пятиугольник. Доказательство. Рассмотрим пятиугольник MPFTN у которого четыре диагонали равны 1 (по теореме 2.1.4 только такой пятиугольник может быть оптимальным). Пусть PN=MT=FM=FN=1, PT=c (рис. 2.2.1). 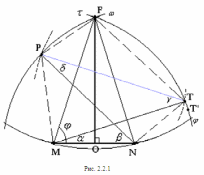 Положим  FMN= FMN= FNM= FNM= , ,  TMN= TMN= , , 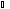 PNM= PNM=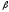 , , 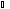 NPT= NPT=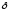 , , 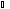 PTM= PTM=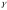 , FO , FO 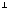 MN. MN.Найдем периметр p пятиугольника MPFTN. Из 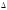 FMO: FMO:MO= cos  , MN=2 cos , MN=2 cos . .Из треугольников 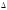 NPF и NPF и 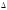 MFT имеем: MFT имеем:PF= 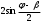 , ,FT= 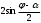 . .Из треугольника 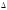 РМТ и РМТ и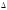 ТNР по теореме косинусов имеем: ТNР по теореме косинусов имеем:PM= 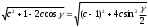 , ,ТN= 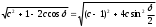 . .Таким образом периметр р пятиугольника MPFTN равен: р=2cos  + +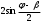 + +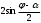 + +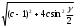 + +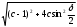 . .Рассмотрим сначала случай, когда с=1, т.е. все диагонали пятиугольника MPFTN равны 1. В этом случае: p=2 cos  + +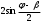 + +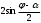 + +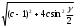 + +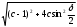 = ==2 cos  + +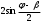 + +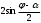 +2sin +2sin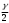 +2sin +2sin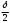 = ==2cos  +4 sin +4 sin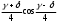 +4sin +4sin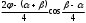   2cos 2cos  +4 sin +4 sin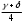 +4sin +4sin =2cos =2cos  +4 sin +4 sin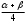 +4sin +4sin = ==2cos  +8sin +8sin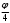 cos cos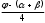  2cos 2cos +8sin +8sin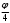 , (т.к. , (т.к. 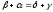 ). ).Исследуем функцию g (  )= 2cos )= 2cos +8sin +8sin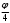 . .g’(  )= (2cos )= (2cos +8sin +8sin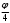 )’= - 2sin )’= - 2sin +2cos +2cos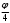 = =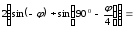 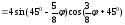 . .Так как 2cos  <1 , то cos <1 , то cos < <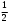 , ,  >60 >60 . .Значит 60  < < <90 <90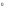 , и мы получаем, что 67,5 , и мы получаем, что 67,5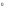 < <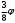 +45 +45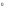 <78,75 <78,75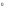 . .Последнее неравенство означает, что ( 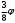 +45 +45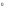 ) - угол первой четверти, т.е. cos( ) - угол первой четверти, т.е. cos(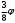 +45 +45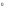 )>0. )>0.sin 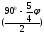 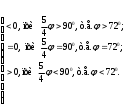 Поэтому p  2cos 2cos +8sin +8sin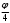  2cos72 2cos72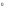 +8sin18 +8sin18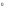 Таким образом, в случае с=1 периметр пятиугольника не превосходит периметра правильного пятиугольника. Рассмотрим теперь случай, когда с<1. Проведем эллипсы через точки Р и Т с фокусами соответственно в точках F, M и F, N. Пусть хотя бы один эллипс пересекает соответствующую дугу  или или (рис. 2.2.1). Пусть, например, эллипс проведенный через точку Т пересекает дугу (рис. 2.2.1). Пусть, например, эллипс проведенный через точку Т пересекает дугу  . Тогда сместив вершину Т в близкую точку Т’ дуги FT, мы получим пятиугольник большего периметра. . Тогда сместив вершину Т в близкую точку Т’ дуги FT, мы получим пятиугольник большего периметра.Остается, следовательно, проверить случай, когда оба эллипса касаются соответствующих дуг. Но из геометрических соображений ясно, что существует не более одной точки дуги  , в которой соответствующий эллипс касается этой дуги (рис. 2.2.2). Тем же свойством обладает симметричная точка дуги , в которой соответствующий эллипс касается этой дуги (рис. 2.2.2). Тем же свойством обладает симметричная точка дуги  . Поэтому, если оба эллипса касаются соответствующих дуг, то . Поэтому, если оба эллипса касаются соответствующих дуг, то 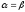 . Оценим периметр пятиугольника в этом случае. . Оценим периметр пятиугольника в этом случае. Рис. 2.2.2 Заметим сначала (рис. 2.2.3), что в виду 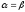 имеем, что PT||MN , откуда имеем, что PT||MN , откуда 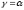 и и 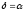 . Проведем NT’ || MT, тогда . Проведем NT’ || MT, тогдаc=PT=PT’-TT’=PT’-MN=2cos  -2cos -2cos . .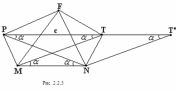 Из 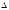 MPT: MPT:PM 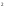 = =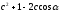 = (2cos = (2cos -2cos -2cos ) ) 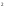 +1-2(2cos +1-2(2cos -2cos -2cos ) cos ) cos = == 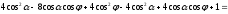 = 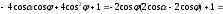 = 1- 2c cos  , то есть , то естьPM= 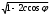 =NT. =NT.Тогда периметр p пятиугольника MPFTN равен: p=2 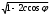 +4sin +4sin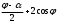 . .Докажем неравенство 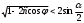 . .Имеем: 1-2c cos  -4sin -4sin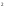  =1-2c cos =1-2c cos -2(1-cos -2(1-cos )=1-2c cos )=1-2c cos -2(1-( -2(1-(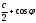 ))= ))==1-2c cos  -2+c+2cos -2+c+2cos =-1+c+2cos =-1+c+2cos (1-c)=( 1- c)(-1+2cos (1-c)=( 1- c)(-1+2cos )<0, )<0,т.к. c<1, (1- c)>0 и 2cos  -1<0, -1<0,  >60 >60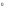 . .Таким образом: 1-2ccos  <4sin <4sin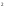 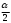 т.е. т.е. 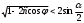 . .Отсюда имеем: 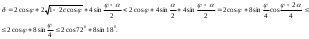 Иначе говоря, периметр пятиугольника MPFTN в этом случае меньше периметра правильного пятиугольника. Таким образом, оптимальным пятиугольником является правильный пятиугольник. Теорема доказана. Заключение Экстремальные задачи — задачи на максимум и минимум — во все времена привлекали внимание учёных. Причина такого интереса заключается, во-первых, в том, что многие экстремальные задачи приходят из практики. Леонард Эйлер (1707-1783), один из величайших математиков, говорил: "В мире не происходит ничего, в чём бы не был виден смысл какого-нибудь максимума или минимума". Во-вторых, среди задач на максимум и минимум много красивых задач, которые интересно и полезно решать. В данной работе рассмотрены различные планиметрические задачи на максимум и минимум, а также изложены основные теоретические сведения, необходимые для решения экстремальных задач. Основное внимание в работе было уделено решению весьма не тривиальной задачи на максимум, а именно отысканию пятиугольника заданного диаметра, имеющего наибольший периметр. При решении поставленной задачи были использованы как геометрические, так и аналитические методы и доказана основная теорема о том, что в пятиугольнике наибольшего периметра по крайней мере четыре диагонали равны единице. В заключительной теореме показано, уже чисто аналитически, что искомым является правильный пятиугольник. Таким образом, основная цель работы достигнута. Библиография 1. Болтянский, В.Г. Теоремы и задачи комбинаторной геометрии [Текст]/ В.Г. Болтянский, И.Ц. Гохберг.- М.: НАУКА, 1965.- 108 с.: ил. 2. Математика, ее преподавание, приложения и история [Электронный документ]/ Я.С. Дубнов, В.Г. Болтянский, В.А. Ефремович и др.; Под ред. Я.С. Дубнов.- вып.3.- М.: Физ.– мат. лит., 1958.- 321 с. 3. Протасов, В.Ю. Максимумы и минимумы в геометрии [Текст]/ В.Ю. Протасов.- М.: НЦНМО, 2005.- 56 с. 4. Тихомиров, В.М. Рассказы о максимумах и минимумах [Текст]/ Тихомиров В.М.- М.: НАУКА, 1986.- 192 с. 5. Трофимов, В.В. Царевна Дидона, изопериметры и мыльные пленки [Электронный документ] (http://mirror1.mccme.ru/kvant/1985/05/carevna_didona_izoperimetry_i.htm) 6. Шклярский, Д.О. Геометрические оценки и задачи из комбинаторной геометрии [Текст]/ Д.О. Шклярский, И.М. Яглом, Н.Н. Ченцов.- М.: НАУКА , 1974.- 384 с.: ил. 7. Энциклопедия элементарной математики [Текст]/ В.Г. Болтянский, В.А. Рохлин, И.М. Яглом, Б.А. Розенфельд и д.р.; Под ред. В.Г. Болтянский.- книга 5.- М.: Физ.– мат. лит., 1966.- 624 с.: ил. 8. Яглом, И.М. Выпуклые фигуры [Текст]/ И.М. Яглом, В.Г. Болтянский.- М.Л.: Гос. изд-во технико-теоретической лит., 1951.- 343 с. |
