Оценка периметра многоугольника заданного диаметра. Реферат По теме "Оценка периметра многоугольника заданного диаметра"

• Название: Реферат По теме "Оценка периметра многоугольника заданного диаметра"
• Дата: 24.11.2022
• Размер: 1.41 Mb.
• Имя файла: Оценка периметра многоугольника заданного диаметра.docx
• Тип: Реферат; #810129
• страница: 3 из 5

Свойство 1.2.1. Всякая максимальная фигура выпукла.

Доказательство.

Пусть хорда А₁В₁, соединяющая точки А₁, В₁нашей фигуры, не лежит целиком внутри нее. Тогда, очевидно, некоторый отрезок этой хорды, скажем АВ,лежит весь (кроме концов) вне фигуры. Можно считать поэтому, что дана фигура с периметром АаВС,равным р,не содержащая хорду АВ (рис. 1.2.1). Заменим дугу а хордой АВ.Периметр при такой замене уменьшится, а площадь увеличится на часть АаВ.Построим теперь фигуру, подобную построенной фигуре А 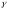ВС, но с периметром, равным периметру первоначальной фигуры АаВС.У новой фигуры площадь будет больше, чем у второй (поскольку коэффициент подобия больше единицы), и подавно больше, чем у первоначальной.

Свойство доказано. [5, 24]

Свойство 1.2.2. Всякая хорда максимальной фигуры с периметром р, делящая пополам ее периметр, обязательно делит ровно пополам и ее площадь.

Доказательство.

Действительно, пусть у фигуры АВСDс периметром р хорда АС делит периметр пополам (рис. 1.2.2). Обозначим через S₁, площадь фигуры AВС,а через S₂ - площадь АDС.Предположим, что S₁>S₂. Построим тогда новую фигуру АВСEА,заменив линию АDС линией АЕС, симметричной с АВС относительно хорды АС.Новая фигура АВСЕА, имея прежний периметр, имеет площадь больше площади первоначальной фигуры, так как площадь новой фигуры равна 2S₁, а площадь первоначальной равна S₁+S₂, в то время как по предположению S₁>S₂ и, следовательно, 2S₁>S₁+S₂. Поэтому фигура АВСDне является, вопреки предположению, максимальной. Это доказывает, что предположение S₁> S₂ неверно. Аналогично доказывается, что и предположение S₁2 приводит к противоречию. Окончательно, S₁= S_2.

Свойство доказано. [3, 31]

Так как при преобразовании подобия площадь плоской фигуры и квадрат ее периметра увеличиваются или уменьшаются в одинаковое число раз и, следовательно, отношение площади к квадрату периметра не меняется, то задачу можно сформулировать следующим образом:

Среди всех плоских фигур найти фигуру, для которой отношение площади к квадрату периметра было бы наибольшим.[8, 67]

В задаче 1.2.5 доказывается, что если выпуклая фигура Ф отлична от круга, то существует фигур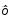а , имеющая тот же самый периметр, что и Ф, и большую площадь. При этом в задаче 1.2.5 утверждается, что такой фигурой может быть только круг. Таким образом, может показаться, что задача 1.2.5 полностью решает изопериметрическую задачу. Однако, хотя это заключение и является верным (см. задачу 1.2.6), пока мы не имеем оснований делать это заключение с полной определенностью: задача 1.2.5 подсказывает ответ изопериметрической задачи, но не дает ее решения. Яркий пример, показывающий, что существование решения надо доказывать,доставляет следующая модификация парадокса Перрона:

Теорема 1.2.1. Среди всех квадратов наибольшую площадь имеет квадрат со стороной 1.

Доказательство

Пусть наибольшую площадь имеет квадрат со стороной a. Рассмотрим два случая: а<1 и a>1. Если а<1, то а²<1 и площадь квадрата со стороной а не является наибольшей (она меньше площади единичного квадрата). Если же а>1, мы возьмем квадрат со стороной b=а². Тогда b>а (так как а> 1), и площадь квадрата со стороной bбудет b², притом b² >а² (так как b>а). Значит, квадрат со стороной а не имеет наибольшую площадь, вопреки предположению.

Теорема доказана. [5, 23]

В доказательстве этой теоремы допущена ошибка, а именно не доказано, что существует квадрат наибольшей площади.

Рассмотрим решение задачи Дидоны, пользуясь изопериметрическим свойством круга (см. задачу 1.2.6).

Пусть AВС и А’В’С’ представляют собой полукруг и какую-нибудь другую фигуру, удовлетворяющую всем условиям задачи. Прибавляя к этим фигурам фигуры АDС и А’D’С’, симметричные с первыми относительно осей АС и А’С’,составим две новые фигуры: круг АВСDи отличную от круга фигуру А’В’С’D’,периметры которых равны 2l. Согласно основной теореме об изопериметрах, площадь круга АВСDбольше площади фигуры А’В’С’D’.Поэтому площадь полукруга АВС больше площади фигуры А’В’С’ и полукруг АВС будет решением задачи Дидоны. [5, 25]
2.1 Задачи

Задача №1.2.1.

а) Докажите, что из всех треугольников с двумя заданными сторонами наибольшую площадь имеет тот, у которого эти стороны взаимно перпендикулярны.

б) Докажите, что из двух неравных треугольников, имеющих равные основания и равные углы при противолежащей вершине, большую плошать и больший периметр имеет тот, у которого разность углов при основании меньше (разность боковых сторон меньше); из всех треугольников с данным основанием и данным углом при противолежащей вершине наибольшую площадь и наибольший периметр имеет равнобедренный.

в) Докажите, что из всех параллелограммов с данным острым углом и данным периметром наибольшую площадь имеет ромб.

г) Докажите, что из двух неравных треугольников с одинаковыми основаниями и одинаковыми периметрами большую площадь имеет тот, у которого меньше разность углов при основании (меньше разность боковых сторон); из всех треугольников с данным основанием и данным периметром наибольшую площадь имеет равнобедренный.

д) Докажите, что из всех трапеций с данными основаниями и данным периметром наибольшую площадь имеет равнобокая. [8, 67]

Задача №1.2.2 .

а) Докажите, что из всех треугольников с данным периметром наибольшую площадь имеет равносторонний треугольник.

б) Докажите, что из всех четырехугольников с данным периметром наибольшую площадь имеет квадрат. [7, 335]

Задача №1.2.3.

а) Докажите, что среди всех n-угольников, вписанных в данную окружность, правильный имеет наибольшую площадь.

б) Докажите, что среди всех n-угольников, вписанных в данную окружность, правильный имеет наибольший периметр. [6, 63]

Задача №1.2.4 .

а) Докажите, что из всех выпуклых четырехугольников с данными углами и данным периметром наибольшую площадь имеет четырехугольник, в который можно вписать окружность

б) Докажите, что из всех выпуклых n-угольников с данными углами и данным периметром наибольшую площадь имеет n-угольник, в который можно вписать окружность. [8, 68]

Задача №1.2.5. Докажите, что если выпуклая фигура Ф отлична от круга, то существует фигура 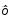, имеющая тот же самый периметр, что и Ф, и большую площадь. [8, 71]

Задача №1.2.6. Докажите, что круг имеет большую площадь, чем каждая другая фигура того же периметра. [6, 67]
2.2 Решения

Задача №1.2.1

а) Утверждение задачи совершенно очевидно (см. рис. 1.2.3)


Рис. 1.2.3
б) Наложим два треугольника, удовлетворяющих условию задачи, друг на друга, чтобы их основания совпали, вершины С и С’ были расположены по одну сторону от общего основания АВ и чтобы одновременно выполнялись следующие условия: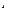
САВ< СВА, С’АВ< С’ВА (рис. 1.2.4, а)

В этом случае вершины С и С’ треугольников будут расположены на дуге окружности ВС’СА,вмещающей угол АСВ,равный углу АС’В (по условию задачи).Из рис. 1.2.4, а)сразу видно, что вершина треугольника АВС,имеющего меньшую разность углов при основании, чем треугольник АВС’,расположена ближе к середине дуги ВС’СА,откуда следует, что высота АВС больше высоты АВС’, и, следовательно, S _АВС>S _АВС’.

Нам остается еще доказать, что:
СА — СВ < С’А— С’В;

и СА+СВ >С’А+С’В.
Отложим на стороне СА отрезок СD=СВ и на стороне С’А отрезок С’D’= С’В и соединим D и D’с В (рис. 1.2.4,а).Так как углы АDВ и АD’Bэтовнешние углы равнобедренных треугольников BCD и BC’D’ то:
ADB=2d- = ,гдеd=90°.

AD’B=d+ .
Так как ADB = АD’В,то точки D и D’ лежат на дуге окружности BD’DA.Поскольку DВА < D’ВА < 180°, то CA-CB=DA<D’A=C’A-C’B.

Аналогично, отложив на продолжении сторон BC и BC’ отрезки CE=CA и C’E’=C’A (рис. 1.2.4, б) получим:
СА+СВ = ВЕ> ВЕ’ = С’А+ С’В,

так как АЕВ= .
Второе утверждение задачи сразу следует из доказанного.

в) Параллелограмм с данным острым углом а и данным периметром 2р разбивается диагональю на два треугольника. Поэтому для решения задачи нам достаточно доказать, что из всех треугольников с данным углом а при вершине и данной суммой р боковых сторон наибольшую площадь имеет равнобедренный треугольник.

Итак, пусть АВС — такой разносторонний треугольник, что:
ВАС = а,а АВ+АС = р;
предположим для определенности, что АВ>АС (в противном случае доказательство аналогично). Построим равнобедренный треугольник АВ’С’,у которого В’АС’ = а, АВ’+АС’ = р и который расположен, как указано на рис. 1.2.5. Точку пересечения сторон ВС и В’С’ обозначим через М.Докажем теперь, что:
S _CC’M>S _BB’M

Действительно, треугольники СС’М и ВВ’М имеют равные углы при вершинах и равные основания СС’ и ВВ’:
СС’ — ВВ’ = (АС’ — АС) — (АВ — АВ’)= (АВ’ +АС’)— (АВ + АС) =р — р = 0.
Далее, из четырех углов ВВ’М, В’ВМ, СС’М и С’СМ наибольшим является первый, а следовательно, наименьшим — второй (т.к. сумма двух первых углов равна сумме двух последних). Отсюда следует, что разность углов при основании треугольника ВВ’М больше, чем разность углов при основании треугольника СС’М.Таким образом S _CC’M>S _BB’M. Следовательно, S _AB’C’>S _ABC , что и требовалось доказать. [8, 221]

г) Наложим два треугольника, удовлетворяющих условию задачи, друг на друга так, чтобы их основания совпали, вершины С и С’ были расположены по одну сторону от общего основания АВ,пусть при этом:
САВ< СВА;

С’АВ< С’ВА,
пустькроме этого
САВ> С’AB(рис.1.2.6).

Если бы при этом был СВА> С’ВА,то C’BAбыл бы заключен внутри треугольника ABCи они не могли бы иметь равных периметров. Следовательно, треугольники расположены так, как изображено на рис. 1.2.6; отсюда и из предыдущих соотношений между углами следует, что разность углов при основании больше у треугольника АС’В ( CBA- CAB < CBA- C’AB< C’BA- C’AB). Точку пересечения сторон АС’ и ВС обозначим через М.Отложим на прямой МА отрезок MN=MBи на прямой МС отрезок МР=МС’. При этом точка N будет находиться между А и М,так как из того, что:
МВА > САВ > МАВ, следует, что МА > МВ.
С другой стороны, точка Р будет находиться между М и С,так как если бы она совпала с некоторой точкой Р’ на продолжении МС,то из равенства периметров двух треугольников мы имели бы
АС+СВ=АС’+С’В, т.е. АС+Р’М-СР’+МВ = АN+NМ+MC’+С’В.
Отсюда, так как:
Р’М=МС’, МВ=МNи С’В=Р’N,
мы имели бы:
АС=АN +NР’+Р’С,
что невозможно.

Отняв теперь от треугольников АВС и АВС’ равные между собой треугольники NМР и МВС’ (заштрихованные на рис. 1.2.6), мы сразу обнаружим, что треугольник АВС имеет большую площадь.

Нам еще остается доказать, что:
СА — СВ< С’А — С’В.
Для этого достаточно проверить, что АС<АС’ (а следовательно, ВС>ВС’). Действительно, если бы было АС>АС’, ВС<ВС’, то из рассмотрения треугольников АСС’ и ВСС’ мы получили бы два несовместных неравенства:

АСС’< АС’С, ВСС’> ВС’С.
Равенство же АС=АС’ невозможно, так как треугольники АВС и АВС’,по предположению, не равны.

Второе утверждение задачи сразу следует из доказанного. [8, 223]

д) Для того чтобы при заданных условиях площадь трапеции АВСDбыла наибольшей, необходимо, чтобы ее высота была наибольшей. Проведя линию ВD’ || СD(рис. 1.2.7), мы получим, что наибольшей высоте трапеции АВСDотвечает наибольшая площадь треугольника АВD’ с заданным основанием (равным разности оснований трапеции) и заданным периметром (равным периметру трапеции минус удвоенное меньшее основание). После этого остается только применить к треугольнику АВD’ заключение задачи 1.2.1 пункта г. [8, 224]

Задача №1.2.2

а) Эта несложная задача имеет несколько решений, мы рассмотрим только два.

Первое решение.

По формуле Герона площадь S треугольника со сторонами a, b, с и полупериметром р равна:
S=
откуда:
S²=p( p-a)( p-b)( p-c).
Но так как:
(p-a)+(p-b)+(p-c)=3p-(a+b+c)=3p-2p=p,
то по теореме о среднем арифметическом и среднем геометрическом:
(p-a)(p-b)(p-c)
и, следовательно, S² , где равенство имеет место лишь в случае p-a=p-b=p-c, т.е. в случае a=b=c, - когда ABC является равносторонним. [6, 253]

Второе решение

Пусть АВС—неравносторонний треугольник, АВ— его большая сторона (или одна из двух больших сторон) (рис. 1.2.8, а).


Рис. 1.2.8
Равнобедренный треугольник АВС’,имеющий тот же периметр, что и треугольник АВС,и то же основание АВ (рис. 1.2.8, а), в силу задачи 1.2.1 г) имеет не меньшую площадь, чем треугольник АВС.Построим теперь треугольник АDЕ, у которого сторона АDравна периметра треугольника АВС’ (или АВС), DАЕ= ВАС’ и периметр которого равен периметру АВС’.Расположим треугольник АDЕ так, как указано на рис. 1.2.8, б).Так как АВ — большая сторона треугольника АВС,а сторона АDравна трети периметра этого треугольника, то АВ>АD;отсюда следует, что АЕ>АС’ (так как иначе АDЕ был бы заключен внутри треугольника АВС’ и не мог бы иметь того же периметра). Так как АВ это большая сторона равнобедренного треугольника АВС’,поэтому:
=AD.
Из последнего неравенства вытекает, что АС’D> АDС’,т. е. ЕС’D< ВDС’.

Так как, кроме того, очевидно, что ВDС’> ЕDС’,то в силу задачи 1.2.1 г) мы можем заключить, что из двух треугольников С’DЕ и ВС’D,имеющих общее основание и равные периметры (т.к. периметр треугольника АВС’ равен периметру треугольника АDЕ,то AC’+C’E+ED+DA = AC’+C’B+BD+DA,значит C’E+ED=C’B+BD), второй имеет меньшую площадь. Таким образом,
S _{C’ DE}>S _{BC’ D}, S _{A DE}>S _ABC’.
Теперь, построив на основании АDравнобедренный треугольник АDF, имеющий тот же периметр, что и треугольник АDЕ (этот треугольник, изображенный пунктиром на рис. 1.2.8, б),очевидно, будет равносторонним (т.к. AD= p, AF=FD= p), мы получим согласно задаче 1.2.1 г), что:

S _ADF > S _ADE
(треугольник АDЕ не совпадает с равносторонним треугольником АDF,так как 60°).

Цепь неравенств:
S _ABC S _ABC’< S _ADE < S _ADF
и доказывает теорему (в этом ряду неравенств мы один раз вынуждены писать вместо <, так как у нас нет уверенности, что АВС не равен AВС’,т. е. что он не равнобедренный). [8, 225]


Рис. 1.2.9
б) Разобьем четырехугольник АВСDдиагональю АС на два треугольника. Заменив треугольники AВС иАСDравнобедренными треугольниками АВ’С и АСD’ с теми же основаниями и с теми же периметрами, мы получим четырехугольник АВ’CD’, причем в силу задачи 1.2.1 г):
S_AB’CD’ S_ABCD (рис. 1.2. 9, а).
Теперь заменим равные треугольники АВ’D’ и В’СD’ (по трем сторонам)равнобедренными треугольниками А’В’D’ и В’С’D’ с теми же основаниями и теми же периметрами; мы получим ромб А’В’С’D’,причем:
S_{A’B’C’D ’} S_AB’CD’ (рис. 1.2.9, б).
Наконец, ромб А’В’С’D’ имеет в силу задачи 1.2.1 а) не большую площадь, чем квадрат А’’B’С’D’’ с той же стороной (рис. 1.2.9, в).

Если четырехугольник АВСDотличен от квадрата, то в цепи неравенств:
S_ABCD S_AB’CD’ S_{A’B’C’D’} S_{A’’B’C’D’’},
хотя бы один раз должно стоять точное неравенство. [8, 227]