Реферат Применение критерия устойчивости Найквиста. мотс реферат. Реферат по теме Применение критерия устойчивости Найквиста
 Скачать 188.38 Kb. Скачать 188.38 Kb.
|
2 Критерий устойчивости НайквистаВ 1932 году Найквист предложил принципиально новый критерий устойчивости. В отличие от критерия Гурвица, который устанавливает принадлежность корней к левой полуплоскости для любого полинома или алгебраического уравнения, критерий Найквиста предназначен для исследования устойчивости только замкнутых систем. [3] Критерий Найквиста — это графоаналитический критерий. Характерной его особенностью является то, что вывод об устойчивости или неустойчивости замкнутой системы делается в зависимости от вида амплитудно-фазовой (а. ф. х.) или логарифмических частотных характеристик (л. ч. х.) разомкнутой системы. [3] Помимо исследования устойчивости по виду указанных характеристик можно оценить и некоторые качественные показатели замкнутой системы, например, запас устойчивости. Более того, появляется возможность указать, как и за счет каких средств неустойчивая замкнутая система может быть сделана устойчивой и как можно повысить качество устойчивой замкнутой системы. Передаточная функция разомкнутой системы может быть представлена в виде 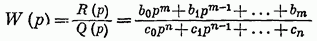 (11) (11)причем степень числителя не может быть выше степени знаменателя, m ≤ n. При подстановке p = jω получается частотная передаточная функция разомкнутой системы Рациональная дробь (11) содержит в числителе характеристический полином замкнутой системы 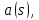 а в знаменателе — характеристический полином разомкнутой системы а в знаменателе — характеристический полином разомкнутой системы 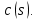 Положим Положим 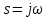 тогда тогда При изменении 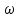 от 0 до от 0 до 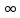 угол поворота вектора угол поворота вектора 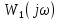 где 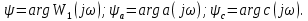 Известно, что в устойчивой системе 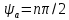 . Угол . Угол 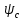 можно определить можно определить 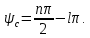 Итак Следовательно, для устойчивой системы вектор 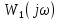 при изменении при изменении 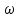 от 0 до от 0 до 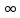 повернется на угол повернется на угол 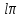 в положительном направлении — против часовой стрелки. Так как функция в положительном направлении — против часовой стрелки. Так как функция 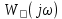 отличается от функции отличается от функции 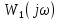 на —1 (рис. 4), то для устойчивой замкнутой системы вектор на —1 (рис. 4), то для устойчивой замкнутой системы вектор 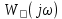 при изменении при изменении 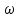 от 0 до от 0 до 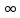 повернется на угол повернется на угол 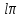 относительно точки (-1, j0). Иными словами, а.ф.х. разомкнутой системы должна охватывать относительно точки (-1, j0). Иными словами, а.ф.х. разомкнутой системы должна охватывать 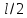 раз точку (-1, j0). Если а.ф.х. строится для диапазона изменения раз точку (-1, j0). Если а.ф.х. строится для диапазона изменения 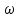 от от 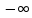 до + до +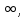 то угол охвата точки (-1, j0) увеличивается вдвое, т. е. [5] то угол охвата точки (-1, j0) увеличивается вдвое, т. е. [5]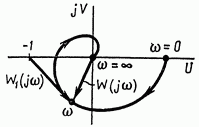 Рисунок 4 – К построению а. ф. х. разомкнутой системы  Рисунок 5 – Годографы устойчивой замкнутой системы: а — разомкнутая система неустойчива  ; б — разомкнутая система устойчива ; б — разомкнутая система устойчива  На основании изложенного критерий устойчивости Найквиста может быть сформулирован следующим образом. Замкнутая САУ устойчива, если при изменении  от 0 до от 0 до  разомкнутой системы [годограф разомкнутой системы [годограф  ] охватывает 1/2 раз точку (-1, j0) в положительном направлении, где I — число корнейхарактеристического уравненияразомкнутой системы, лежащих в правойполуплоскости.[5] ] охватывает 1/2 раз точку (-1, j0) в положительном направлении, где I — число корнейхарактеристического уравненияразомкнутой системы, лежащих в правойполуплоскости.[5]Если разомкнутая система устойчива  то для устойчивости замкнутой системы нужно, чтобы а.ф.х. разомкнутой системы не охватывала точку (-1, j0). На рис. 5 показан вид годографов то для устойчивости замкнутой системы нужно, чтобы а.ф.х. разомкнутой системы не охватывала точку (-1, j0). На рис. 5 показан вид годографов  соответствующих устойчивой замкнутой системе. соответствующих устойчивой замкнутой системе. Некоторые особенности применения критерия Найквиста появляются при исследовании устойчивости систем, нейтральных в разомкнутом состоянии, т. е. имеющих нулевые корни, а также систем, находящихся в разомкнутом состоянии на колебательной границе устойчивости, т. е. имеющих чисто мнимые корни. Например, если  имеет один нулевой корень, то годограф разомкнутой системы имеет один нулевой корень, то годограф разомкнутой системы  при при  обращается в бесконечность (рис. 6, а). В этом случае для сохранения формулировки критерия, справедливой для устойчивых в разомкнутом состоянии систем, включают нулевой корень в левую полуплоскость, огибая его справа окружностью бесконечно малого радиуса обращается в бесконечность (рис. 6, а). В этом случае для сохранения формулировки критерия, справедливой для устойчивых в разомкнутом состоянии систем, включают нулевой корень в левую полуплоскость, огибая его справа окружностью бесконечно малого радиуса  (рис. 6, б). При этом годограф (рис. 6, б). При этом годограф  уходящий при уходящий при  в бесконечность, дополняется частью окружности бесконечно большого радиуса, которая проводится по часовой стрелке от положительной вещественной полуоси, т. е. на угол в бесконечность, дополняется частью окружности бесконечно большого радиуса, которая проводится по часовой стрелке от положительной вещественной полуоси, т. е. на угол  (рис. 6, а). [3] (рис. 6, а). [3]При нескольких нулевых корнях, т. е. при более высоком порядке астатизма системы, угол дополнения а.ф.х. окружностью бесконечно большого радиуса составляет (рис. 7) где – порядок астатизма (число нулевых корней характеристического уравнения разомкнутой системы). Аналогичные дополнения а.ф.х. дугами окружности бесконечно большого радиуса приходится производить и при наличии чисто мнимых корней в характеристическом уравнении разомкнутой системы, так как в этих случаях а.ф.х. также имеют разрывы непрерывности.  Рисунок 6 – Годограф системы, имеющей в разомкнутом состоянии один нулевой корень (а) и отнесение нулевого корня к левой полуплоскости (б) Дополнение производится полуокружностью бесконечно большого радиуса о часовой стрелке, начиная от той ветви а.ф.х. (имеющей разрыв непрерывности), которая соответствует меньшим частотам. Это изображено на рис. 7. На рис. 7, а показана а. ф. х. разомкнутой системы, устойчивой в замкнутом состоянии. А. ф. х. построена только для положительных частот. При частоте  а. ф. х. уходит в бесконечность, асимптотически приближаясь к прямой, составляющей с осью вещественных угол, равный а. ф. х. уходит в бесконечность, асимптотически приближаясь к прямой, составляющей с осью вещественных угол, равный  . . Рисунок 7 – А. ф. х. нейтральных разомкнутых систем, дополненных дугами бесконечного радиуса: а — система с астатизмом второго порядка; б — система с астатизмом третьего порядка Далее а. ф. х. дополнена полуокружностью бесконечного радиуса, и при  она возвращается на бесконечности вдоль той же асимптоты. Дальнейший ход а. ф. х. является обычным. [6] она возвращается на бесконечности вдоль той же асимптоты. Дальнейший ход а. ф. х. является обычным. [6]Из рис. 8, а видно, что а. ф. х. разомкнутой системы не охватывает точку (-1, j0). В данном случае это должно соответствовать устойчивой замкнутой системе. [6] На рис. 8, б изображен другой случай, когда расположение а. ф. х. таково, что в замкнутом состоянии система оказывается неустойчивой, так как а. ф. х. охватывает точку (–1, j0). Достоинством критерия Найквиста является возможность использования для определения устойчивости снятых экспериментально частотных характеристик. Это оказывается особенно ценным в том случае, когда ввиду сложности исследуемой системы трудно получить исходные дифференциальные уравнения всей системы или ее отдельных блоков.[6] Большое практическое преимущество критерия Найквиста заключается также в том, что он может применяться при использовании логарифмических частотных характеристик, которые во многих случаях могут строиться почти без вычислительной работы. Этот вопрос будет рассмотрен в следующем параграфе. [6] Для этой системы была получена передаточная функция разомкнутой системы  (17) (17) Рисунок 8 – А. ф. х. разомкнутой системы, имеющей пару мнимых корней: а — замкнутая система устойчива; б — замкнутая система неустойчива Нетрудно видеть, что все корни знаменателя, кроме одного нулевого корня, лежат в левой полуплоскости. Поэтому в устойчивой системе амплитудно-фазовая характеристика не должна охватывать точку (–1, j0). [7] Широкое распространение критерий Найквиста получил при суждении об устойчивости по логарифмическим частотным характеристикам. Возможность такого суждения вытекает из того, что а.ф.х. разомкнутой системы полностью определяется парой характеристик   или (что то же) или (что то же)  . Точкам пересечения годографа . Точкам пересечения годографа  с отрезком отрицательной вещественной полуоси с отрезком отрицательной вещественной полуоси  соответствуют точки, для которых Точки л.ф.х. соответствуют точки, для которых Точки л.ф.х.  для которых для которых  и в которых она пересекает при увеличении и в которых она пересекает при увеличении  прямые прямые 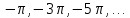 снизу вверх, условимся называть отрицательными переходами, а сверху вниз — положительными переходами л.ф.х. (рис. 9). [7] снизу вверх, условимся называть отрицательными переходами, а сверху вниз — положительными переходами л.ф.х. (рис. 9). [7]Тогда критерий устойчивости может быть сформулирован следующим образом. САУ устойчива, если разность между положительными и отрицательными переходами л.ф.х. равна 1/2 где I — число корней характеристического уравнения разомкнутой системы, лежащих в правой полуплоскости. Для частного случая, когда 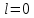 (система устойчива или нейтральна в разомкнутом состоянии), получается, что система устойчива, если разность между положительными и отрицательными переходами равна нулю. (система устойчива или нейтральна в разомкнутом состоянии), получается, что система устойчива, если разность между положительными и отрицательными переходами равна нулю. 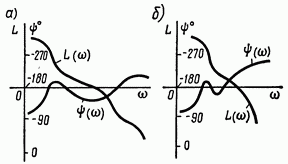 Рисунок 9 – Определение устойчивости по логарифмическим частотным характеристикам: а — замкнутая система устойчива ( 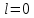 ); б — замкнутая система неустойчива ); б — замкнутая система неустойчива 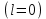 При анализе многоконтурных систем для оценки устойчивости замкнутой системы на практике иногда оказывается удобнее рассматривать не функцию 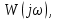 а обратную ей функцию а обратную ей функцию 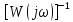 Это может быть целесообразно, например, когда из-за наличия местных обратных связей знаменатель передаточной функции разомкнутой системы W(s) не разлагается на простые сомножители, а числитель представляет собой число или состоит из простых сомножителей и имеет более низкий порядок. В этом случае инверсная (обратная) передаточная функция Это может быть целесообразно, например, когда из-за наличия местных обратных связей знаменатель передаточной функции разомкнутой системы W(s) не разлагается на простые сомножители, а числитель представляет собой число или состоит из простых сомножителей и имеет более низкий порядок. В этом случае инверсная (обратная) передаточная функция 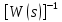 оказывается значительно проще для анализа, чем выражение оказывается значительно проще для анализа, чем выражение  [7] [7]Кривая, описываемая концом вектора  при изменении частоты от при изменении частоты от  до до  называется обратной (инверсной) а.ф.х. Инверсная а.ф.х. строится по выражению обратной частотной передаточной функции. называется обратной (инверсной) а.ф.х. Инверсная а.ф.х. строится по выражению обратной частотной передаточной функции. При использовании инверсной а.ф.х. формулировка критерия Найквиста изменяется. Для случая устойчивой в разомкнутом состоянии системы, когда все полюсы функции 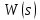 и все нули функции и все нули функции 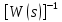 расположены в левой полуплоскости, критерий Найквиста формулируется следующим образом: для устойчивости замкнутой системы необходимо и достаточно, чтобы обратная а.ф.х. охватывала точку с координатами (–1, j0) при изменении частоты от расположены в левой полуплоскости, критерий Найквиста формулируется следующим образом: для устойчивости замкнутой системы необходимо и достаточно, чтобы обратная а.ф.х. охватывала точку с координатами (–1, j0) при изменении частоты от 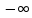 до до 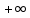 . . |
