Реферат Применение критерия устойчивости Найквиста. мотс реферат. Реферат по теме Применение критерия устойчивости Найквиста
 Скачать 188.38 Kb. Скачать 188.38 Kb.
|
3 Применение критерия Найквиста к системам с неустойчивыми звеньямиПри наличии неустойчивого звена функция K(p) будет иметь n-кратный полюс в точке p=a, где Re a > 0. Предположим для определенности, что точка а расположена на действительной оси. При построении контура в плоскости pвыключим полюс а при помощи окружности l малого радиуса r, проходимой против стрелки часов. В плоскости К ей будет соответствовать кривая , близкая к окружности бесконечно большого радиуса, описываемой n раз по стрелке часов. Поэтому, при применении критерия Найквиста, нужно дополнить контур 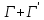 бесконечно большой окружностью, описываемой n раз по стрелке часов. бесконечно большой окружностью, описываемой n раз по стрелке часов. 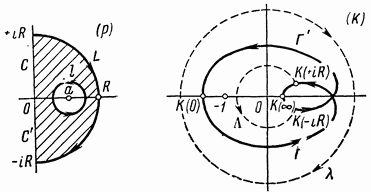 Рисунок 10 – Диаграмма Найквиста относится к устойчивой системе, у которой точка p=a Это следует из того, что в окрестности полюса p=a функция K(p) ведет себя как 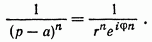 (19) (19)В случае наличия неустойчивого звена имеет место следующее соотношение: Изображенная на рис. 10 диаграмма Найквиста относится к устойчивой системе, у которой точка p=a является полюсом первого порядка (n=1). Во всех рассмотренных в пп. 3 и 4 случаях формула оказывается верной, если простые полюсы во внутренних точках правой полуплоскости считать за единицу, а на мнимой оси — за половину; кратные полюсы соответственно за n и n/2. 4 Применение критерия Найквиста к системам с нейтральными звеньямиОбъекты управления могут быть нейтральными или неустойчивыми (паровая машина, корабль, нейтральный или статически неустойчивый самолет) и задача регулирования состоит в превращении их в устойчивые системы. Среди звеньев регулятора также встречаются нейтральные (серводвигатели). При наличии нейтральных элементов точка p=0 будет полюсом функции K(p), и при построении контура в плоскости p этот полюс нужно обойти по малой полуокружности l радиуса r (рис. 11). [10] 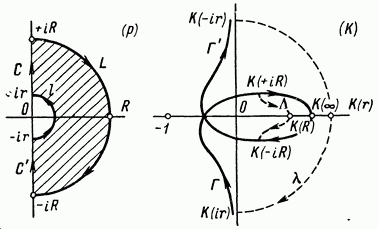 Рисунок 11. Если точка p=0 — полюс первого порядка, то в ее окрестности Функция K(p) ведет себя как 1/p, и аргументам +i0, -i0 функции K(i 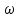 )соответствуют ветви кривых Г, )соответствуют ветви кривых Г, 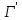 , уходящие в бесконечность вдоль мнимой оси. Полуокружность lотображается на кривую, близкую к полуокружности бесконечно большого радиуса, описываемую по стрелке часов и смыкающуюся с бесконечными ветвями кривых Г, , уходящие в бесконечность вдоль мнимой оси. Полуокружность lотображается на кривую, близкую к полуокружности бесконечно большого радиуса, описываемую по стрелке часов и смыкающуюся с бесконечными ветвями кривых Г, 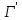 . Когда . Когда 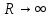 , дуга , дуга 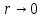 , отображающая полуокружность l, стягивается в точку , отображающая полуокружность l, стягивается в точку 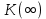 , а дуга , отображающая малую полуокружность l, уходит в бесконечность. [9] , а дуга , отображающая малую полуокружность l, уходит в бесконечность. [9]В итоге опять остается кривая 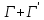 , бесконечные ветви которой нужно представлять себе замкнутыми полуокружностью бесконечно большого радиуса, расположенной в правой полуплоскости К. К полученному замкнутому контуру по-прежнему применяем критерий Найквиста. [10] , бесконечные ветви которой нужно представлять себе замкнутыми полуокружностью бесконечно большого радиуса, расположенной в правой полуплоскости К. К полученному замкнутому контуру по-прежнему применяем критерий Найквиста. [10]Диаграмма Найквиста, изображенная на рис. 11, относится к устойчивой системе, у которой точка p=a является полюсом первого порядка. Для показанного на рис. 11 случая имеет место соотношение Показанная на рис. 12 диаграмма Найквиста относится к устойчивой системе, у которой точка p=0 является полюсом 2-го порядка.[10] 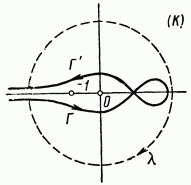 Рисунок 12 – Диаграмма Найквиста Если точка p=0 есть полюс n-го порядка, то кривая 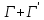 должна быть замкнута бесконечно удаленной линией, состоящей из n полуокружностей, пробегаемых по стрелке часов. Это следует из того, что в окрестности точки p=0 функция K(p) ведет себя должна быть замкнута бесконечно удаленной линией, состоящей из n полуокружностей, пробегаемых по стрелке часов. Это следует из того, что в окрестности точки p=0 функция K(p) ведет себя 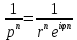 то есть полярный угол в плоскости К вn раз больше полярного угла в плоскости p. В рассматриваемом случае имеет место соотношение то есть полярный угол в плоскости К вn раз больше полярного угла в плоскости p. В рассматриваемом случае имеет место соотношение Заключение На основании освоения полученной темы, можем сказать, что критерий Найквиста относится к группе частотных критериев, поскольку определяет устойчивость замкнутых систем по их частотным характеристикам. Его особенностью является возможность применения к замкнутым системам с запаздыванием, которыми является подавляющее большинство систем управления. Библиографический списокБессекерский, В.А., Теория систем автоматического регулирования: учебное пособие / В.А. Бесекерский, Е.П. Попов. – 4-е изд., перераб. и доп. – СПб.: Изд-во «Профессия», 2004. – 752 с. Основы автоматического регулирования и управления: учебн. пособие для неэлектротехн. специальностей вузов. / под ред. В. М. Пономарева, А. П. Литвинова. – М.: «Высшая школа», 1974. – 439 с. Теория автоматического управления. Учеб. для вузов по спец. "Автоматика и телемеханика". В 2-х ч./ Н.А. Бабаков, А.А. Воронов и др.; под ред. А.А. Воронова. – 2-е изд., перераб. и доп. – М.: Высш. шк., 1986. – 367с., ил. Ляпунов, А.М. Общая задача об устойчивости движения: дис. и статьи / А.М. Ляпунов. – 2-е изд. – М.: ОНТИ. Гл. ред. общетехн. лит., 1935. – 386 с. Ройтенберг, Я. Н. Автоматическое управление: учебное пособие / Я. Н. Ройтенберг. – М., Изд-во «Наука», 1971. – 396 с. Егоров, К.В. Основы теории автоматического регулирования: учебное пособие для вузов. / К.В. Егоров. – изд. 2-е, перераб. и доп., - М.: "Энергия", 1967. – 648с., ил. Куропаткин, П.В. Теория автоматического управления: Учеб. пособие для электротехн. спец. вузов. / П.В. Куропаткин. – М.: "Высшая школа", 1973. – 528 с., ил. Лазарева, Т. Я. Основы теории автоматического управления: Учебное пособие. / Т. Я. Лазарева, Ю. Ф. Мартемьянов. – 2-е изд., перераб. и доп. – Тамбов: изд-во Тамб. гос. техн. ун-та, 2004. – 352 с. Дорф, Р. Современные системы управления / Р. Дорф, Р. Бишоп. пер. с англ. Б. И. Копылова. – М.: Лаборатория Базовых Знаний, 2002. – 832 с.: ил. Теория автоматического управления: учеб. для машиностроит. спец. вузов / В.Н. Брюханов, М.Г. Косов, С.П. Протопопов и др.; Под ред. Ю.М. Соломенцева. – 3-е изд., стер. – М.: Высш. шк.; 2000. – 268 с: ил. |
