Курсовая работа Ринат. Реферат пояснительная записка л., рис., табл., источника
 Скачать 0.65 Mb. Скачать 0.65 Mb.
|
|
СОДЕРЖАНИЕ 1 Литературный обзор 5 2 Проектировочный расчет балки на статическую прочность 6 2.1 Построение эпюр внутренних силовых факторов 6 2.2 Подбор сечения стальной балки 9 2.3 Подбор сечения чугунной балки 12 3 Полная проверка прочности двутавровой балки 18 4 Расчет двутавровой балки на жесткость 22 РЕФЕРАТ Пояснительная записка … л., … рис., … табл., … источника. ДВУТАВРОВАЯ БАЛКА, ПОПЕРЕЧНАЯ СИЛА, ИЗГИБАЮЩИЙ МОМЕНТ, РАСЧЕТ, ПРОЧНОСТЬ, ЖЕСТКОСТЬ, ПРОГИБ, УГОЛ ПОВОРОТА Объектом проектирования является двутавровая стальная балка. Цель проектирования: закрепление теоретических знаний, полученных при изучении дисциплины “Прикладная механика”. Выбор сечения балки произведен по соответствующим нормативным источникам. Расчеты балки выполнены по методу начальных параметров, методу Мору и способу Верещагина. Спроектированная балка может использоваться в различных конструкциях и сооружениях. ВВЕДЕНИЕ Цель данной курсовой работы является практический расчет на жесткость и прочность элементов конструкций, работающие на растяжение и сжатие. Из условия жесткости и прочности выявляем оптимальные значения размеров разных вариантов поперечного сечения элементов конструкций. При работе будем использовать методы науки “Сопротивление материалов”, то есть вести практический расчет и определять жесткость балок при деформации. Данная тема курсовой работы поможет определять максимальные нагрузки на балки, так как во многих конструкциях и сооружениях применяются данные типы балок. 1 Литературный обзорВ ходе выполнения курсовой работы обращаемся к теоретическим обоснованиям данной разработки. Изгиб – это такой вид нагружения, при котором в поперечных сечениях стержня возникают изгибающие моменты [1]. В зависимости от возникающих в балке внутренних силовых факторов различаем чистый и поперечный изгиб. Поперечный изгиб считается более опасным, чем чистый, так как в поперечном изгибе кроме изгибающего момента также возникает поперечная сила. В общем случае при изгибе часть слоев бруса удлиняется, а другая часть укорачивается [2]. При полной проверки на прочность балки при изгибе по трем типам опасных точек рассматриваем расчетную схему простой балки с эпюрами поперечной силы Q и изгибающего момента Миз, находя при этом реакции опор. Выполняя подбор сечений стальной и чугунной балок, определяем геометрические характеристики сечения [1]. Для нахождения перемещений в упругих системах используем метод Мора. Преимуществом метода Мора является то, что он позволяет находить различные перемещения для сложных систем. Недостаток в трудоемкости при расчете систем с большим количеством силовых участков. Для уменьшения трудоемкости интеграл Мора заменяют произведением в соответствии со способом Верещагина, согласно которому искомое перемещение представляет собой произведение площади грузовой эпюры на ординату единичной эпюры, которая располагается по центром тяжести грузовой эпюры на данном участке [3]. 2 Проектировочный расчет балки на статическую прочность2.1 Построение эпюр внутренних силовых факторовВычерчиваем схему нагружения (рисунок 2.1). Определяем реакции опор и строим эпюры поперечной силы и изгибающего момента. Направив реакции опор в точке С и В вверх (горизонтальная реакция Hс=0), составим уравнения моментов относительно опор     Для проверки составим уравнение проекций всех сил на ось y 0,09qa+0,91qa-0,5qa-0,5qa=0; 0,91qa-0,91qa=0; 0=0. Условие проверки выполняется. Разбиваем балку на четыре силовых участка ВТ, ТА, АС, СК. Для каждого участка применяем метод сечений и составляем уравнения поперечной силы и изгибающего момента I Участок ВТ 0≤z1˂0,5а 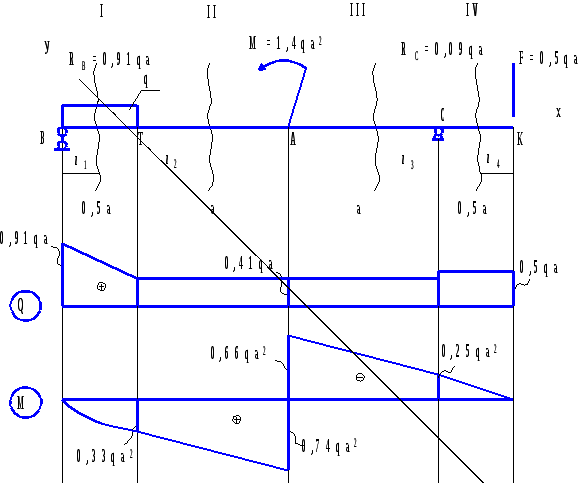 Рисунок 2.1 – Схема нагружения балки и эпюры Q и M   II Участок ТА 0≤z2˂а  III Участок АС 0≤z3˂а  IV Участок СК 0≤z4˂0,5а  По полученным результатам строим эпюры Q и M (рисунок 2.1). Эпюра изгибающего момента построена на растянутом волокне. Выполняем проектировочный расчет стальной балки из условия прочности по нормальным напряжениям при изгибе   где Mи max – максимальный изгибающий момент, по эпюре моментов получим Тогда  2.2 Подбор сечения стальной балкиПо расчетному моменту сопротивления Wx выполняем подбор сечений стальной балки. Стальное двутавровое по ГОСТ 8239-98 (рисунок 2.2); по сортаменту выбираем двутавр №18, для которого Wx=143 см3, площадь сечения двутавра Адв=23,4 см2, осевой момент инерции Ix=1290 см4, статический момент сопротивления меньше табличного значения, следовательно, недонагрузка двутаврового сечения составляет Стальное прямоугольное, при  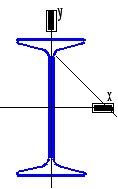 Рисунок 2.2 – Двутавровое сечение Получим сторону основания прямоугольника   Принимаем «b» кратное двум, то есть b=58 мм, тогда h=2·58=116 мм. Площадь прямоугольного сечения Апр=b·h; Апр=58·116=6728 мм2=66,28 см2. Стальное круглое (рисунок 2.4)  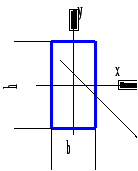 Рисунок 2.3 – Прямоугольное сечение   По стандартному ряду принимаем d=108 мм. Тогда площадь круглого сечения   Выполняем оценку экономичности сечений стальной балки, сравнивая их вес по соответствующим величинам площадей Адв:Апр:Акр=23,4:66,28:91,61=1:2,83:3,915. 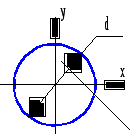 Рисунок 2.4 – Круглое сечение Таким образом, самым целесообразным является двутавровое сечение. 2.3 Подбор сечения чугунной балкиЧугунное Т-образное сечение (рисунок 2.5). Предварительно найдем геометрические характеристики сечения. 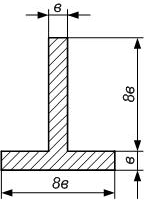 Рисунок 2.5 – Сечение чугунной балки Определим площадь сечения А1=8b·b=8b2; А2=b·8b=8b2; А=А1+А2=8b2+8b2=16b2. Координата x – центра тяжести сечения. у1=0,5b; у2=b+0,5·8b=5b;  Осевой момент инерции сечения   а1=у1-x=0,5b-2,75b=-2,25b; a2=у2-x=5b-2,75b=2,25b; Ix=0,667·b4+(-2,25b)2·8b2+42,667b4+(2,25b)2·8b2=124,3b4. Осевые моменты сопротивления для верхних и нижних точек сечения    По этим значениям Wx вычислим, во сколько раз напряжения в верхних волокнах больше, чем в нижних.   Рационально расположим поперечное сечение балки. По эпюре Мизг (рисунок 2.1) видим, что в опасном сечении растягиваются нижние волокна. Учитывая, что чугун – хрупкий материал и хуже сопротивляется растяжению, чем сжатию, расположим сечение так, чтобы в нем растягивающие напряжения имели меньшую величину, чем сжимающие, то есть следующим образом (рисунок 6). Проведем подбор сечения из условия прочности по растягивающим напряжениям    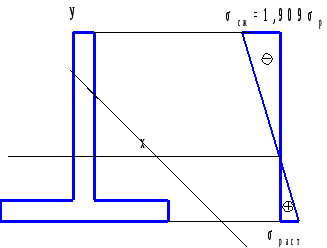 Рисунок 2.6 – Расположение сечения  Принимаем «b» кратное 2, то есть b=28 мм. По полученному значению b проверим сечение на прочность по сжимающим напряжениям   Прочность балки обеспечивается. Сравнение сечений балки Построим все сечения одном масштабе с эпюрами нормальных напряжений в опасном сечении балки (рисунок 2.7);  Для стального двутаврового сечения при площади Адв=23,4·10-4 м2. Для стального прямоугольного сечения   ˂ ˂при площади Апр=66,28 см2=66,28·10-4 м2. Для Т-образного сечения имеем   ˂ ˂А=16b2; А=16·2,82=125,44 см2. Анализируя эпюры нормальных напряжений (рисунок 2.7), видим, что все сечения удовлетворяют условию прочности, но наиболее экономичным является двутавровое сечение, на что указывает следующее соотношение площадей Адв:Апр:Акр:АТ=23,4:66,28:91,61:125,44. 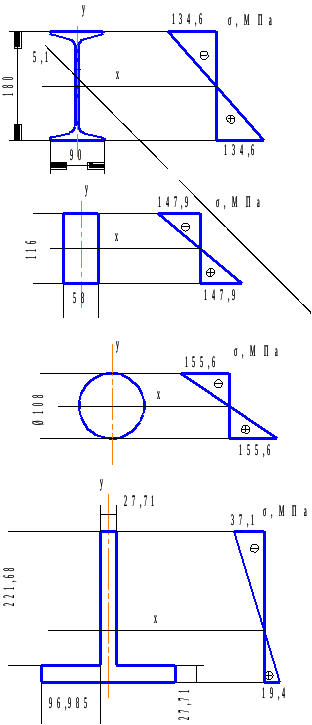 Рисунок 2.7 – Сечения с эпюрами нормальных напряжений в опасном сечении балки М(1:5) 3 Полная проверка прочности двутавровой балкиРасчет на прочность по опасным точкам второго типа двутавровой балки выполняется из условия прочности  Qmax=0,91qa; d=b(y)=0,51 см; Ix=1290 см4; Sxотс=81,4 см3; Подставляя числовые значения в формулы, получим  Условие прочности выполняется. Для балки двутаврового профиля проведем полную проверку прочности, выбрав наиболее опасное сечение, где одновременно возникает большой изгибающий момент и поперечная сила Qопас=0,41qa; M=0,74qa2. Расчет нормальных, касательных и главных напряжений по опасным точкам третьего типа Для полной проверки прочности построим эпюры нормальных (σ), касательных (τ) и главных (σ1, σ3) напряжений, используя следующие формулы    Для двутаврового сечения из сортамента по ГОСТ 8239 – 97 выбираем значения осевого момента инерции и сопротивления Ix=1290·10-8 м4; Sx=81,4·10-6 м3. Результаты расчета приводим в табличной форме (таблица 3.1). Таблица 3.1 – Результаты расчета напряжений в точках опасного сечения двутавровой балки
По полученным значениям строим эпюры нормальных, касательных и главных напряжений в опасном сечении балки (рисунок 3.1). Графическое определение главных напряжений. Проверка прочности для опасных точек третьего типа Для опасной точки 2', где σ1=0,83 МПа, σ3=-123,33 МПа, производим поверку прочности по четвертой теории прочности 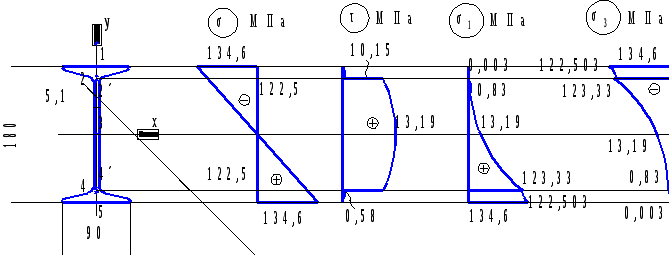 Рисунок 3.1 – Эпюры напряжений в опасном сечении балки Подставляя числовые значения, получим то есть условие прочности выполняется. Для точки 4' сечения графически найдем величины главных напряжений пр помощи круга Мора (рисунок 3.2) Сравнивая значения σ1 и σ3 найденные аналитически и графически, видим, что они практически равны σ1ан=σ1граф=123,33 МПа; σ3ан=σ3граф=-0,83 МПа. 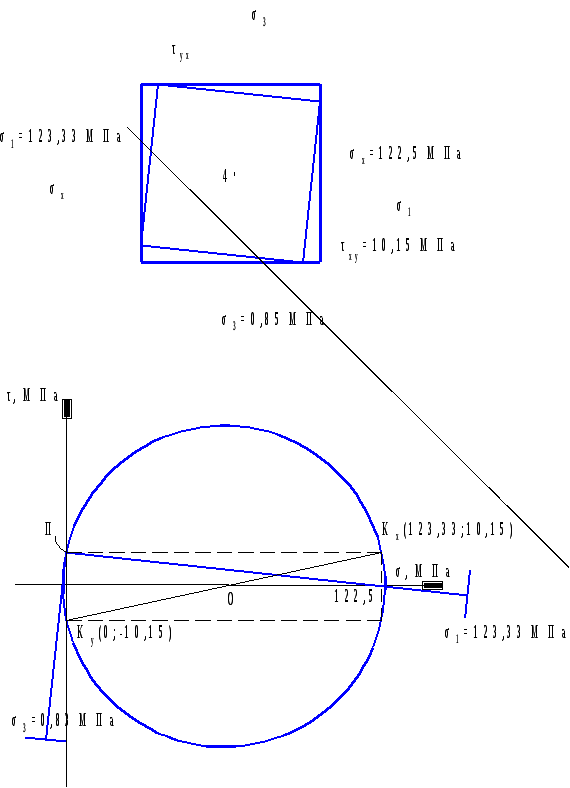 Рисунок 3.2 – Определение главных напряжений при помощи круга Мора 4 Расчет двутавровой балки на жесткостьРасчет прогибов и углов поворота балки по методу начальных параметров Пользуясь универсальным уравнением упругой линии балки (УУУЛБ), рассчитаем прогибы и углы поворота по методу начальных параметров. 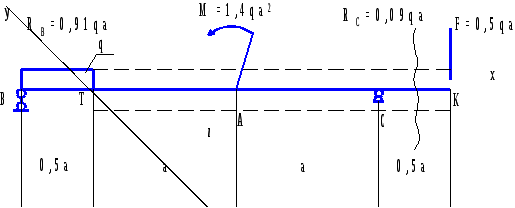 Рисунок 4.1 – Расчетная схема для определения прогибов и углов поворота точек балки Выбираем систему осей координат с началом точки В=0. Составляем УУУЛБ для силового участка  Найдем начальные параметры у0 и  у0=уВ=0. При z=2,5a, прогиб на опоре в точке С уС=0, тогда  отсюда  Отсюда найдем угол поворота в начале координат  Подставляем полученные начальные параметры в исходное УУУЛБ  Найдем прогиб в точке К  Подставляя числовые значения, получим    Найдем прогиб в точке Т  Подставляя числовые значения, получим   Найдем прогиб в точке А  Подставляя числовые значения, получим   Универсальное уравнение углов поворота балки УУУПБ имеет вид  Преобразуем УУПБ, подставляя полученные начальные начальные параметры  Подставим числовые значения, получим, найдем угол поворота на опоре в точке В  Найдем угол поворота на опоре в точке С  Подставляя числовые значения, получим    По полученным данным строим эпюру прогибов (рисунок 4.2). 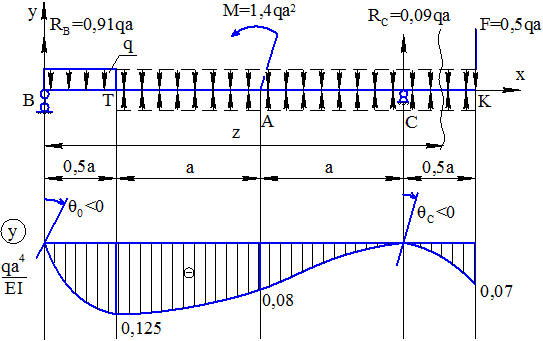 Рисунок 4.2 – Упругая линия балки Расчет перемещений методом Мора. Пользуясь методом Мора определим прогиб у в точке Т и угол поворота 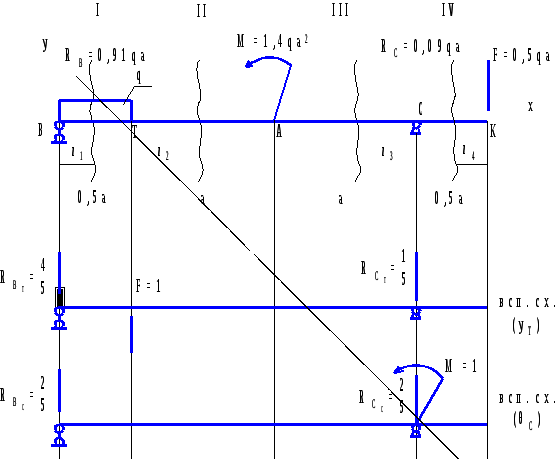 Рисунок 4.3 – Вспомогательные схемы для определения прогиба и угла поворота по методу Мора Для исходной и вспомогательных схем составляем уравнение изгибающих моментов, соответственно, грузовых и единичных для силовых участков. Уравнения грузовых моментов можно представить в следующем виде  Составим уравнения единичных моментов для прогиба в точке Т, предварительно определив реакции опорных связей для данной вспомогательной балки. Единичные моменты для уТ   Определяем прогиб в точке Т по методу Мора для чего воспользуемся интегралом Мора  Подставляем соответствующие грузовые и единичные моменты по участкам     Угол поворота для       Определение перемещений точек двутавровой балки по способу Верещагина Выбираем вспомогательные схемы, которые загружаются соответствующими единичными нагрузками в искомых точках (рисунок 4.4). Определяя искомые перемещения по способу Верещагина, используем формулу  Для этого перемножаем грузовую эпюру на соответствующие единичные      Тогда   Угол поворота в точке В  Тогда   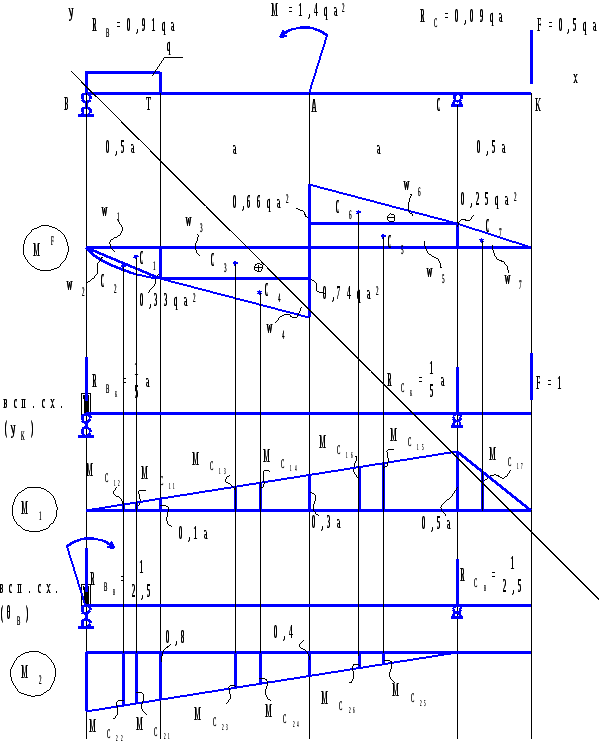 Рисунок 4.4 – Расчет перемещений по способу Верещагина Проверка условий жесткости балки Выполним проверку жесткости балки по линейным и угловым перемещениям, для этого запишем условия жесткости для опасных точек балки   Подставляя числовые значения, получим   Условия жесткости выполняются. Сравнение перемещений в точках балки, найденных по МНП, ММ и СВ представлены в таблице 4.3 Таблица 4.3 – Сравнение перемещений по МНП, ММ и СВ
ЗАКЛЮЧЕНИЕ В курсовой работе произведен расчет двутавровой стальной балки на статическую прочность и жесткость при изгибе. Рассмотрены основные понятия и положения по теории изгиба. Произведен расчет на прочность стальных балок двутаврового, прямоугольного, круглого и Т-образного сечения. В сравнении рассчитанных сечений по экономичности использования материала подтвердило целесообразность двутаврового профиля № 18. Для этой балки выполнена полная проверка прочности по опасным точкам 3-х типов, рассчитаны линейные и угловые перемещения точек балки по методу начальных параметров, методу Мора и способу Верещагина, сравнение которых подтвердило их сходимость с допустимой погрешностью. Выполнили проверку условий жесткости балки и доказали ее работоспособность. Согласно заданию составлен соответствующий иллюстрационно-графический материал (формат А2 и формат А3). СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 1 Феодосьев, В.И. Сопротивление материалов: Учеб. Для вузов. - 11-е изд., стереотип. – М.; Изд-во МГТУ им. Н.Э. Баумана, 2003. – 592 с. (Сер. Механика в техническом университете; Т.2). 2 Газиев, Р.Р. Расчет конструкций при изгибе. Учебное пособие. – Уфа: Изд-во УГНТУ, 2003. – 60 с. 3 Феодосьев, В.И. Сопротивление материалов. – М.: Изд-во. МГТУ им. Н.Э. Баумана, 1999 – 592 с. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
