реферат. Реферат Выпускная квалификационная работа содержит 5 глав, написанных в 106

• Название: Реферат Выпускная квалификационная работа содержит 5 глав, написанных в 106
• Анкор: реферат
• Дата: 06.02.2023
• Размер: 2.82 Mb.
• Имя файла: реферат.docx
• Тип: Реферат; #922688
• страница: 15 из 20

Оценка возможности использования термофлуктуационной теории для анализа полученных результатов

В литературном обзоре было показано, что для описания зависимостей времени до пробоя от температуры и напряженности электрического поля может быть использована термофлуктуационная теория разрушения, в основе которого лежит механизм разрушения за счет разрыва химических связей в материале под действием температуры и других нагрузок. В данной работе нами произведен расчет параметров уравнения кривой жизни на использовании методики, описанной в [12].

Для расчета параметров используем полученные нами результаты по измерению времени до пробоя, приведенные в таблице 3.5 при двух температурах и напряженности электрического поля.

Расчет проводится с использованием программы Mathcad.

1. 
   Рассчитываем вероятность безотказной работы P(t)
   

i
𝑃 = ^𝑛−i+0.5, (3.2)

𝑛+0.5

где n– число образцов, i– номер образца.

2. 
   Значения х находим из условия равенства функции F(x) и f(x)
   

𝐹 = 2 · 𝑘 · ^𝑇 · ( ^𝑡 ), (3.3)

𝐷 𝑡0





^{(𝑥) =} √^{1 − 2𝑥 − 𝑥 *1 1} √^{1 − 2𝑥 − 1+,(3.4)}

𝑥 𝑥
где – постоянная Больцмана; t0-постоянная времени, с..

3. 
   Для нахождения значений х при известной величине f(x) воспользуемся функцией вида V1(x1,t1) и V2(x2,t2) соответственно при начальных значениях х1 = 0,01 и х3 = 0,01
   

𝑉⁽𝑥, 𝑡⁾ = ⁽𝑥⁾ − 2 · 𝑘 ·^𝑇 , (3.5)

𝑡0

4. 
   Тогда значение (х) найдем как функцию Z1, Z3соответственно:
   

𝑍_i = 𝑟𝑜𝑜𝑡(𝑉⁽𝑥, 𝑡⁾, 𝑥), (3.6)

5. 
   Найдем параметры уравнения надежности из следующих условий. В cлучае однородного электрического поля η=1, т.к. у нас неоднородное поле, то η=1.3, β1=2
   
6. 
   При каждой вероятности пробоя находим b и его математическое ожидание:
   

i
𝑏1 = ¹

𝑇3−𝑇1

· ln (^Z1i), (3.7)

Z3_i

𝑏1 = ^∑i𝑏1i = 0,013.

𝑛

7. 
   Находим параметр Апо результатам испытаний первой партии и соответственно значениях β1 при t1 E=E1
   

¹ ·𝑒^{−𝑏1·𝑇1}·𝑦·𝐸1·𝛽1
𝐴1 =^Z1i= 3,67 · 10⁻²⁶, (3.8)

𝐷

¹·A1·e^-b1·T1·𝜂·E1
𝛽1=^Z1i=2. (3.9)

D

8. 
   Рассчитаем врeмя до пробоя при температуре Т1 и напряженности поля Е1, на основе найденных параметров уравнения надежности.
   

Найденные параметры: b1=0,013; β1=2; A1=3,67 10^-26; Е1=4,41 10^-26В/м. Постоянные: D=5,5 10^-1 Дж/св; k=1,38 10^-23Дж/К^о; t0=1 10^-13сек.


𝐷
𝑥_𝑇1 = ¹ · 𝐴1 · 𝑒^{−𝑏1·𝑇1} · 𝛽 · 51 · 𝐸1, (3.10)

^{фT1 =} √^{1 − 2 · 𝑥𝑇1 − 𝑥𝑇1 · ln ( 1}


𝑥
𝑇1

₊ 1

^𝑥𝑇1



^· √^{1 − 2 · 𝑥𝑇1 − 1), (3.11)}

𝑟1 = 𝑡0 · 𝑒𝑥𝑝 (^{𝐷·𝑥𝑇1} ), (3.12)

2·𝑘·𝑇1
Где t0– постоянная времени, с; k– постоянная Больцмана, Дж/К^о; D– энергия разрыва химической связи, Дж; (х)– функция от действующих нагрузок (х), вызывающих уменьшение потенциального барьера; A- параметры уравнения, определяемые экспериментально;  - коэффициент, учитывающей повышение напряженности электрического поля за счет формы электродов;  - коэффициент, учитывающий повышение напряженности электрического поля за счет неоднородности структуры материала диэлектрика; Е – напряженность приложенного электрического поля, [В/м]; b – коэффициент, учитывающий изменение модуля упругости материала с температурой, 1/К^о.
С точки зрения термодинамики известно, что τ₀ 10^-13 с, т.е. время перехода атомов из одного равновесного состояния в другое за счет тепловых флуктуаций.

По тем же формулам и рассчитаем время до пробоя при температуре Т3 и напряженности поля Е1: 𝑥_𝑇3 = 0,03 ; ф_𝑇3 = 0, 2 ; 𝑟1 = ,3 1 · 10³,c.

9. 
   Построили график зависимости времени до пробоя от температуры при напряженности поля Е1 по рассчитанным значениям и нанесем точки средних значений времени до пробоя τср1 и τср3 по данным эксперимента и для сравнения точки времени до пробоя τ_Т1 и τ_Т3, полученные расчетным путем при температуре Т1 и напряженности поля Е1.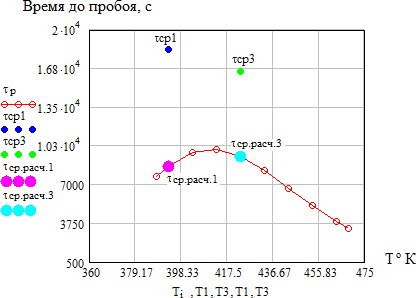
   

Рисунок 3.8 – График зависимости времени до пробоя от температуры при напряженности поля Е1 по расчетным значениям.

10. 
    Построим график зависимости времени до пробоя от температуры при напряженности Е1 с учетом значения среднего времени до пробоя τср4 при температуре Т4= 100°С.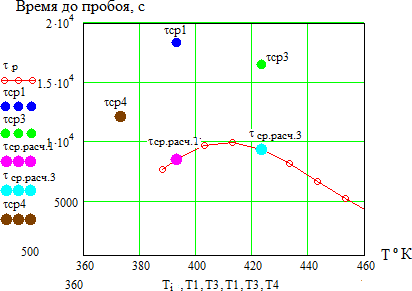
    

Рисунок 3.9 – Зависимость времени до пробоя от температуры при напряженности Е1 с учетом значения среднего времени до пробоя τср4

Из полученного графика видно, расчетные и экспериментальные значения среднего времени до пробоя несколько отличаются. Расчетная кривая дает заниженные значения времени до пробоя, что может быть связано с неточностью расчета параметров и коэффициентов без учета реальных условий старения.

Из приведенных рис. 3.8 и 3.9 можно также отметить, что характер зависимости, построенный, по расчетным данным имеет вид кривой с максимумом. Такой же характер изменения времени до пробоя наблюдается по экспериментальным данным.

11. 
    Проанализируем зависимость времени до пробоя от напряженности поля при различных температурах Т1 и Т3 на основе термофлуктуационной теории.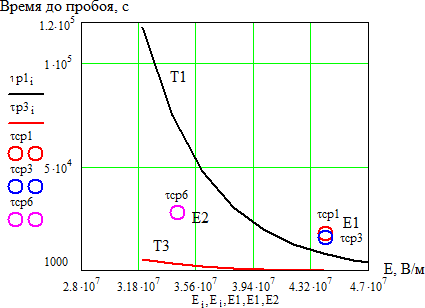
    

Рисунок 3.10 – Зависимость времени до пробоя от напряженности поля при различных температурах Т1 и Т3 на основе термофлуктуационной теории.

Из данного графика видно, что изменение напряженности электрического поля значительно сильнее оказывает влияние на характер кривой. Однако можно отметить, что экспериментальные точки среднего времени до пробоя лежат в растворе полученных кривых зависимости времени до пробоя от напряженности поля при различных температурах Т1 и Т3.

12. 
    Учитывая неточность нахождения параметров уравнения надежности, уточним значения этих параметров из условия полученных данных и проанализируем зависимость времени до пробоя от напряженности электрического поля и температуры согласно термофлуктуационной теории. Зная значения среднего времени до пробоя на основе экспериментальных данных при разных температурах и напряженностях поля найдем коэффициент ф(х) по формуле
    

1 1
_{ɸ5 =} ⁽ln⁽𝑐cp1⁾⁾−ln⁽𝑐cp3⁾·2·𝑘 _{= 0,03. (3.13)}

𝐷·( − )



T1 T3
После уточнения найденных параметров проанализируем зависимость времени до пробоя от температуры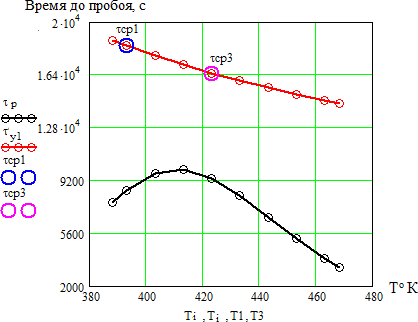


Рисунок 3.11 – Зависимость времени до пробоя от температуры после уточнения найденных параметров

Из приведенного рисунка 3.11 видно, что по уточненным параметрам кривая зависимости времени до пробоя от температуры хорошо согласуется с экспериментальными данными и данными из литературного обзора.

В литературном обзоре нами было также показано, что для описания зависимостей времени до пробоя от температуры и напряженности электрического поля можно использовать различные эмпирические уравнения. Произведем расчет коэффициентов, входящих в эти уравнения и для сравнения рассчитаем зависимости времени до пробоя от температуры и напряженности электрического поля.

13. 
    Оценим зависимость времени жизни от напряженности электрического поля согласно уравнениям степенного вида, которое имеет вид:
    

i
𝑟_𝑐t = 𝐴_ct · 𝐸^−𝑚, (3.14)
Параметры для данного уравнения найдем, таким образом:

_{𝑚 =} ⁽log⁽𝑐cp6⁾ − log⁽𝑐cp4⁾⁾ _{= 3,386; 𝐴}ct ₌ 𝑐cp6



= 9,3 · 10²⁹, (3.15)

⁽log⁽𝐸1⁾−log⁽𝐸2⁾⁾

_𝐸2−𝑚

Где τср– среднее время до пробоя при Т4; τср6 – среднее время до пробоя при Т6; Е_i – задаем произвольно.

Строим графики зависимости времени жизни cm от напряженности электрического поля для уравнения степенного вида, согласно расчетным данным (рисунок 3.12).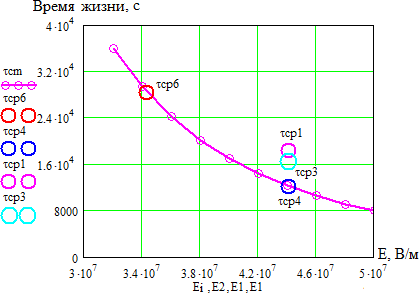



Рисунок 3.12 – Зависимость времени жизни от напряженности электрического поля для уравнения степенного вида, согласно расчетным данным (здесь τсm –кривая времени жизни; τср1, τср3, τср , τср6– среднее время до пробоя при Т= 120, 150, 100 ^оС)

Как видно из данного графика, экспериментальные значения времени до пробоя при температуре 100°С совпадают с расчетной зависимостью от напряженности электрического поля по уравнению степенного вида.

14. 
    Проанализируем зависимость времени жизни ek от напряженности электрического поля на основе уравнения экспоненциального вида
    

𝑟 = 𝐵 · 𝑒^−𝑏𝐸, (3.16)

где В и b параметры, отражающие свойства изоляции.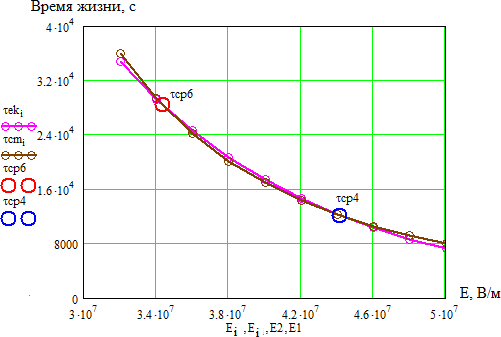



Рисунок 3.14 – зависимость времени жизни ek от напряженности электрического поля на основе уравнения экспоненциального вида

Как видно из приведенного рисунка 10 расчетные зависимости времени до пробоя практически совпадают и имеют одинаковый характер.

15. 
    Оценим изменение времени жизни k от напряженности электрического поля на основе комбинированного уравнения, учитывающего действие приложенного напряжения и температуры:
    

∆W

𝑟 = 𝐶 · 𝑈^−𝑁 · 𝑒 ^𝑘𝑇 . (3.17)
Находим величину ∆W при постоянстве напряженности поля

∆W

₌ ⁽ln⁽𝑐cp1⁾⁾−ln⁽𝑐cp3⁾ _{= 8,12 · 10−21. (3.18)}


1 1
( − )

T1·𝑘 T3·𝑘
Значение постоянной N находим при постоянстве температуры
_{𝑁 =} ⁽ln⁽𝑐cp6⁾⁾−ln⁽𝑐cp4⁾ _{= 3,386, (3.19)}

ln⁽𝑈2⁾−ln⁽𝑈1⁾

𝐶 =
𝑐𝑐𝑝3


∆Wк

_𝑈2^−𝑁_·𝑒𝑘·𝑇3

= 1,007 · 10¹⁷, (3.20)

где k – постоянная Больцмана; U1, U2 – напряженности поля.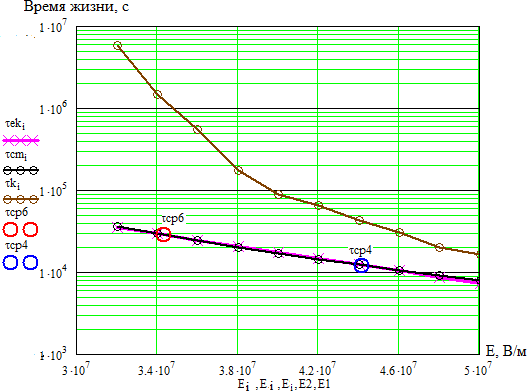


Рисунок 3.15 – Зависимость времени жизни k от напряженности электрического поля на основе комбинированного уравнения

Уравнение комбинированного вида в отличие от уравнений степенного и экспоненциального вида позволяет оценить влияние на время до пробоя, как температуры, так и напряженности электрического поля.

Однако из приведенного рисунка 3.15 видно, что рассчитанная зависимость на основе уравнения комбинированного вида от кривых, рассчитанных на основе уравнения экспоненциального вида, а экспериментальные значения среднего времени до пробоя не укладываются на данную кривую.

Таким образом, можно сказать, что зависимость времени до пробоя может быть описаны как эмпирическими уравнениями, так и на основе термофлуктуационной теории. Однако использование эмпирических

уравнений не дает физического объяснения закономерностям электрического старения и практически наталкивается на большие затруднения, связанные с отсутствием в литературе значений параметров изоляции входящих в эти уравнения, а также отсутствием условий, в которых проводились исследования [1].