Гдз. Занятие №14 ПСА 216. Занятие 14 Решение тригонометрических уравнений Однородные уравнения. Уравнение вида
 Скачать 490.8 Kb. Скачать 490.8 Kb.
|
|
ЗАНЯТИЕ № 14 Решение тригонометрических уравнений Однородные уравнения. Уравнение вида 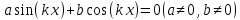 называется однородным уравнением первой степени. Оно решается делением обеих частей уравнения на называется однородным уравнением первой степени. Оно решается делением обеих частей уравнения на 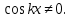 Потери корней в этом случае не будет, так как при Потери корней в этом случае не будет, так как при 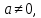 однородному уравнению не удовлетворяют те значения однородному уравнению не удовлетворяют те значения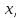 при которых при которых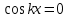 . В результате получится уравнение вида: . В результате получится уравнение вида: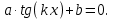 Можно разделить обе части данного однородного уравнения на 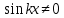 , в результате чего получится уравнение вида , в результате чего получится уравнение вида 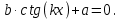 Пример 1. Решить уравнение 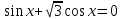 .|: .|: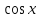 Решение. Разделим обе части уравнения на 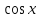 , , 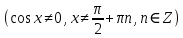 получим: получим: 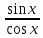 + +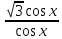 = = 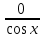  Ответ: 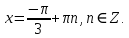 Пример 2. Решить уравнение 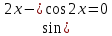 . .Решение. Разделим обе части уравнения на 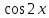 , ,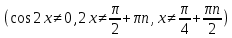 , получим: , получим: 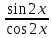 - - 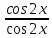 = = 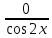 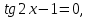 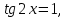 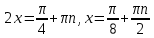 , ,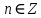  Ответ: Ответ: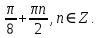 Пример3. 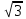 sin x cos x + sin x cos x + 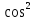 x = 0 x = 0Решение. cos x ∙ ( 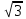 sin x + cos x)= 0 sin x + cos x)= 0cos x = 0 или 2) 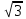 sin x + cos x= 0 sin x + cos x= 0x = 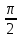 + + 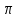 k k 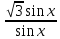 + +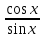 = = 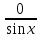 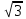 + ctg x = 0, ctg x = - + ctg x = 0, ctg x = - 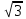 , tg x = - , tg x = - 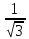 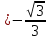 x = 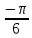 + + 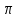 n nОтвет: 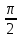 + + 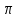 k; k; 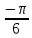 + + 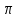 n n Решить однородное уравнение sin 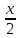 + + 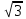 ∙ cos ∙ cos 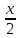 =0 =0cos ( 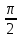 - - 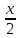 ) - ) - 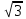 ∙cos (π - ∙cos (π - 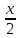 ) =0 ) =03) sin ( 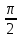 +2x) + cos ( +2x) + cos (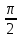 -2x) =0 -2x) =02.Уравнения вида 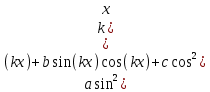 называется однородным уравнением второй степени, если 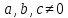 или какие - либо два из них отличны от нуля. или какие - либо два из них отличны от нуля.Пусть 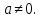 Тогда уравнение решается делением обеих частей на Тогда уравнение решается делением обеих частей на 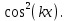 В результате получаем уравнение вида В результате получаем уравнение вида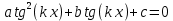 равносильное данному, так как корни уравнения 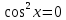 не являются корнями исходного однородного уравнения. не являются корнями исходного однородного уравнения.Пример 1. Решить уравнение:  . .Решение. Разделим обе части уравнения на 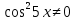 , получим: , получим: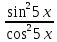 + + 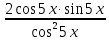 - - 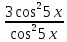 = = 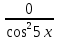 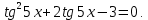 1)Это уравнение, сводящееся к квадратному. Сделаем замену 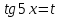 и уравнение примет вид: и уравнение примет вид: 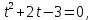 D = 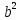 - 4ac = 4 – 4 - 4ac = 4 – 4  1 1  (-3) = 16, (-3) = 16, 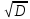 = 4 = 4 2)Пришли к двум уравнениям:  x = - x = - 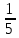 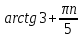 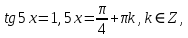 x = x = 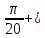 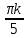 Решить уравнение: 1) 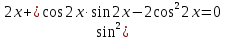 2) 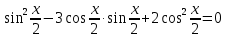 3) 2 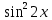 – 5 – 5  = 0 = 04) 3 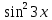 + 10 + 10 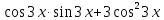 = 0 = 0Пример 2. Решить уравнение 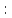 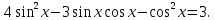
Решение. Представим правую часть уравнения в виде: 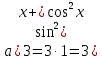 , тогда , тогда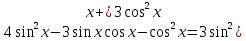 . .Перенесем все слагаемые в левую часть уравнения, приведем подобные слагаемые, получим: 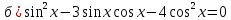 . .Разделим обе части уравнения на  , получим: , получим: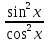 - - 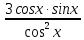 - - 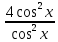 = = 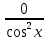 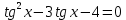 Это уравнение, сводящееся к квадратному. Сделаем замену 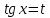 и уравнение примет вид: и уравнение примет вид: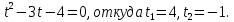 Пришли к двум простейшим уравнениям: 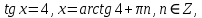 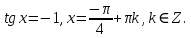 Ответ: 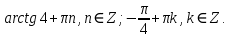 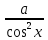 = a(1 + = a(1 + 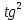 x) x)Решить уравнение: 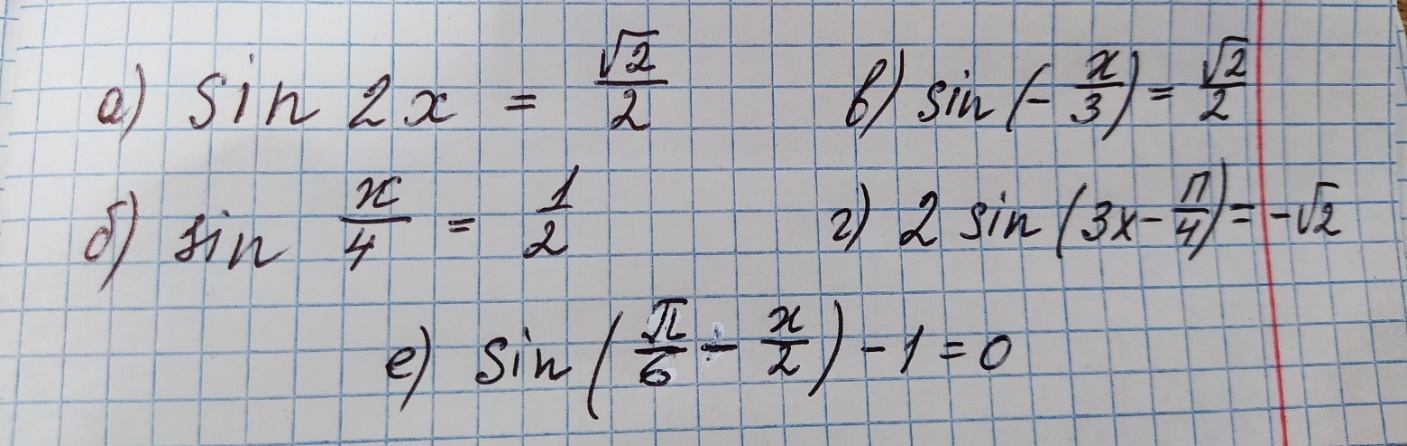 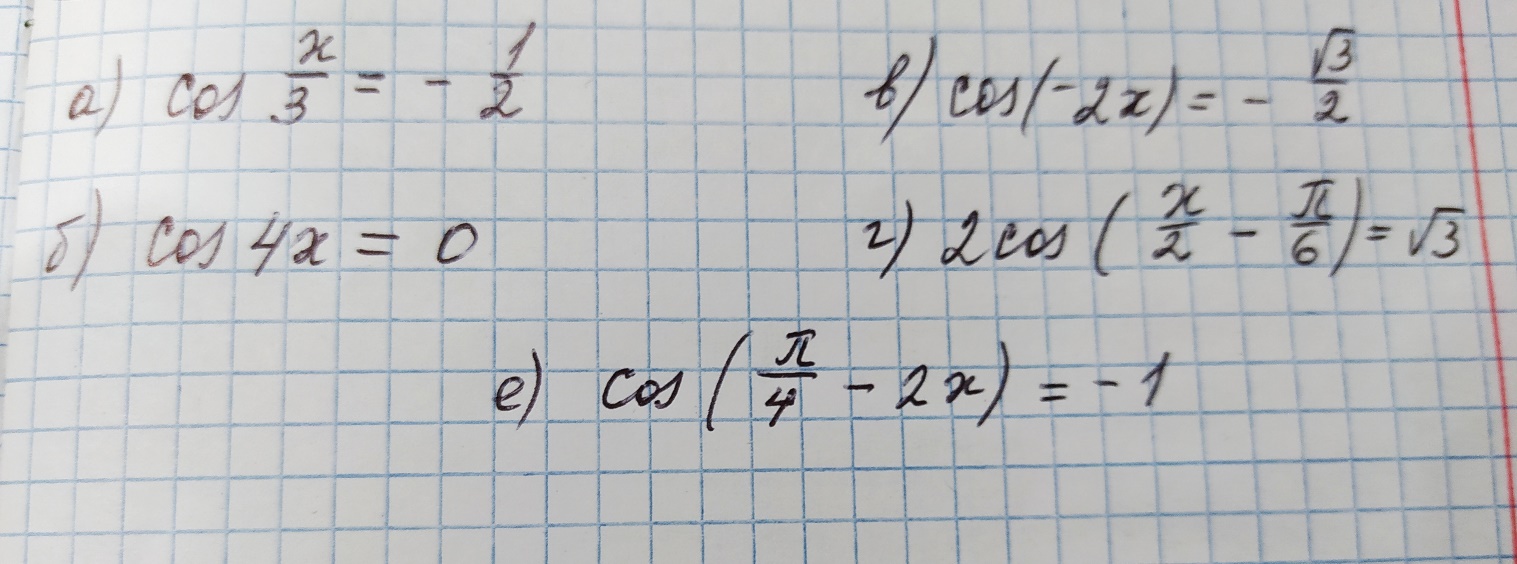 tg (-4x) = 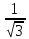 5) 2 5) 2 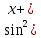 3 cos x = 0 3 cos x = 0ctg (  - - 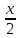 ) = 1 6) 4 sin 3x + ) = 1 6) 4 sin 3x + 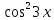 = 4 = 42sin(3x - 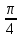 ) = - ) = - 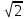 7) 3 7) 3 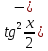 2ctg ( 2ctg ( 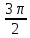 + + 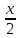 ) – 1 = 0 ) – 1 = 02∙cos( 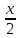 - -  ) = ) =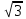 №1 cos ( 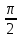 - - 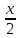 ) - ) - 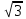 ∙cos (π - ∙cos (π - 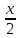 ) =0 №2 sin ( ) =0 №2 sin (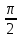 +2x) + cos ( +2x) + cos (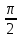 -2x) =0 -2x) =0sin 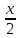 + + 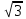 ∙cos ∙cos 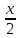 = 0 cos 2x + sin 2x = 0 = 0 cos 2x + sin 2x = 0tg 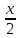 + + 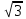 = 0 1 + tg 2x = 0 = 0 1 + tg 2x = 0tg 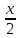 = - = - 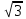 tg 2x = -1 tg 2x = -1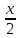 = - = -  + + 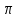 k 2x = - k 2x = - 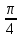 + + 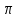 k kx = - 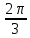 + +  k х = - k х = - 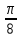 + + 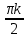 | ||||

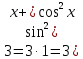 , тогда
, тогда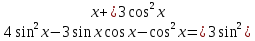 .
.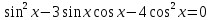 .
.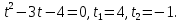

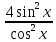 -
- 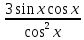 -
- 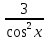
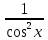 = 1 +
= 1 +