рефрактометрия. Рефрактометрический метод анализа в химии
 Скачать 6.6 Mb.
|
Рис. 3. Зависимость молярной поляризацииот обратной температуры а - для молекулы, постоянных диполей; b - для неполярных молекул. .2 Молярная рефракция Из электромагнитной теории света Максвелла следует, что для длин волн, значительно удалённых от области их поглощения молекулами вещества, справедливо равенство: 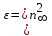 , (18)где n∞ - показатель преломления света для определённых длин волн. С учётом этого уравнение Клаузиуса-Мосотти (15) принимает следующий вид: 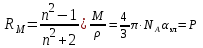 [ см3/(г·моль)] (19)Из полученного выражения видно, что показатель RМ, называемый молярной рефракцией, имеет размерность объёма молекул, содержащихся в 1 моль вещества. Уравнение (15), которое носит название уравнения Лорентца - Лоренца, выведено в 1880 г. независимо друг от друга Х. Лорентцем и Л. Лоренцем. На практике часто пользуются показателем удельной рефракции r, то есть рефракцией одного грамма вещества. Удельная и молярная рефракции связаны соотношением: R = r∙M, где М молярная масса. Поскольку в уравнении (19) N пропорционально плотности, то его можно представить в следующем виде: 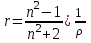 [ см3/г] (20)Х. Лорентц и Л. Лоренц вскрыли физический смысл понятия рефракции - как меры электронной поляризуемости и подвели под учение о рефракции прочный теоретический фундамент. Величина удельной рефракции практически не зависит от температуры, давления и агрегатного состояния вещества. В исследовательской практике кроме молярной и удельной рефракции RМ и r используют и другие производные от показателей преломления n (табл. 2). Показатель преломления неполярных веществ практически не зависит от частоты волн света и поэтому уравнение (19) справедливо при всех частотах. Например, для бензола n2 = 2,29 (длина волны 289,3 нм), тогда как ε = 2,27. поэтому, если для приближённых расчётов рефракции достаточно пользоваться показателем преломления видимого спектра, то для точных расчётов необходимо производить экстраполяцию по формуле Коши: nλ = n∞ + a/λ2, (21) где nλ - показатель преломления при длине волны λ; а - эмпирический коэффициент. Таблица 2 Рефрактометрические константы
Для полярных веществ ε > n2. Для воды, например, n2 = 1,78 (λ = 589,3 нм), а ε = 78. Более того, в этих случаях нельзя непосредственно экстраполировать nλ по формуле Коши вследствие того, что показатель преломления полярных веществ часто аномально изменяется с частотой. Однако обычно нет необходимости производить такую экстраполяцию, так как рефракция является величиной аддитивной и сохраняется, если показатели преломления всех веществ измерять при определённой длине волны. За такую стандартную длину волны выбрана жёлтая линия в спектре натрия (λD = 589,3). В справочных таблицах приводятся данные именно для этой длины волны. Таким образом, для расчёта молекулярной рефракции (в см3/моль) пользуются формулой, в которой n∞ заменён на nD: 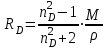 . (22)Обычно индекс D опускают и формулу записывают как уравнение (19). 3. Рефракция и структура молекул .1 Аддитивность рефракции Рефракция, является аддитивной величиной. Использование рефрактометрии в науке было начато в середине XIX века, когда обнаружили, что между молекулярными рефракциями соседних членов гомологического ряда органических соединений выполняется простое соотношение: 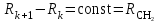 .(23)Согласно этому соотношению молекулярную рефракцию k-го члена гомологического ряда можно представить в виде суммы молекулярных рефракций первого члена ряда и k−1 группы СН2: 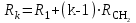 .(24)Впоследствии было обнаружено, что ряд изомеров также имеют одинаковые молекулярные рефракции. Это обстоятельство позволило предположить, что молекулярная рефракция вещества зависит только от природы и числа атомов в молекуле и может быть вычислена простым суммированием характерных для каждого элемента атомных рефракций: 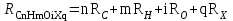 ,(25)где  - молекулярная рефракция органического соединения состава СnHmOiXq;RC, RH и др. - соответственно рефракции атомов углерода, водорода и других элементов (табл. 3). Было установлено и то, что молекулярная рефракция большого числа органических соединений может весьма отличаться от суммы составных рефракций. К простейшим соединениям такого типа относятся этиленовые углеводороды и их алкилпроизводные. Этот класс соединений всё же был включён в аддитивную схему путём учёта того обстоятельства, что в этих соединениях имеются двойные связи типа С=С, аналогично был произведён учёт наличия тройных связей С≡С, которыми характеризуются ацетиленовые соединения. Таким образом, рассчитывая рефракцию молекулы через рефракции составляющих её атомов и фрагментов, следует учитывать валентные состояния атомов - инкременты (вклады) рефракций двойных и тройных связей, а также поправки на особое положение отдельных атомов и атомных групп в молекулах: R = ∑RA + ∑R1, (26) где RА и R1 - соответственно атомные рефракции и инкременты связей (табл. 3, 4). Поляризуемость ионов. В органической химии большое значение имеет поляризуемость анионов. Существует несколько наборов рефракций ионов. Определяемых либо в растворах, либо в твёрдом или газообразном состоянии. 1. Рефракции и, следовательно, поляризуемости увеличиваются с увеличением размера иона в пределах одной группы периодической системы химических элементов. Например: F¯ < Cl¯ < J¯ (табл. 3); ОН¯ < SH¯ (табл. 4). 2. Анионы легче поляризуются, чем соответствующие нейтральные молекулы. Например: SH¯ > H2S; OH¯ > H2O. 3. Анионы с большим зарядом легче поляризуются, чем с меньшим. Например: S2- > SH¯. Наличие координационной (донорно-акцепторной, семиполярной) связи в молекуле вызывает уменьшение рефракции по сравнению с суммой рефракций индивидуальных молекул, образующих эту связь. Например: величины R для (СН3)3N+-B¯F3 и (C2H5)2O+−B¯F3 примерно на 3,5 и 2,0 см3 меньше суммы величин R для этих компонент [(CH3)3N - триметиламина, (С2Н5)2О - диэтилового эфира и BF3 - трёхфтористого бора]. Молекулярная рефракция обычно рассматривается как аддитивно конститутивное свойство. Конститутивный характер этого свойства следует из происхождения этого явления. Однако аддитивный характер совсем не так легко продемонстрировать, поскольку, хотя по определению следует, что рефракция молекул должна равняться сумме рефракций отдельных её частей, не вполне ясно, каким образом выделять эти части. Существуют три различные схемы для определения основных констант. Это система атомных рефракций, рефракций групп и связей. Так, согласно первой, R = ∑rA, где ∑r выражает сумму индивидуальных атомных рефракций. Например, для этилового спирта СН3СН2ОН или диметилового эфира СН3ОСН3 она равна 2r + 5rH + r0. Согласно второй схеме, величина R для этилового спирта определяется как сумма рефракций групп ( 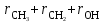 ), в то время как для диметилового эфира эта величина будет равна (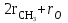 ).Согласно третьей схеме, величина R для этилового спирта будет определяться суммой (5rC−H + rC−C + rO−H), а для диметилового эфира (6rC−H + 2rC−O). Эти схемы не дают идентичных значений для одного и того же соединения, а также ни одна из них не даёт строго аддитивных значений. Схема рефракции связей является наилучшей из всех трёх для определения рефракции органических молекул. Наиболее важное её преимущество перед другими связано с тем, что эта схема облегчает прямой подход к концепции анизотропии поляризации, причём этот термин означает, что поляризуемость орбитали, ориентация которых совпадает с направлением поля, отличается от их поляризуемости при иной ориентации. Само по себе не кажется очевидным, что поляризуемость почти сферических атомов должна изменяться при изменении ориентации молекулы в поле: более очевидным является то, что поляризуемость связей должна изменяться в соответствии с тем - колинеарны они полю или перпендикулярны ему, и удалось добиться некоторых положительных результатов при анализе рефракций связей, представляя их как совокупность продольных, поперечных и вертикальных параметров. Одна из главных трудностей, с которыми приходится сталкиваться, - это решение вопроса о вкладе в общую поляризуемость, вносимом несвязанными парами электронов гетероатомов таких групп, как С-Х, С-О, С-N. Величина R прямо пропорциональна электронной поляризуемости молекул и обладает свойством аддитивности, так что её можно вычислить суммированием ряда постоянных слагаемых Ri, приписываемых содержащимся в молекуле атомам, группам атомов, связям или некоторым особенностям структуры (кратным связям, кольцам) и называемых соответственно атомными, групповыми, связевыми рефракциями и структурными инкрементами: 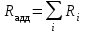 .Так, например, молекулярная рефракция нафтеновых углеводородов (алициклов) СnH2n может быть вычислена как сумма атомных рефракций углерода RC и водорода RH: 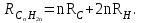 (27)Поскольку основной вклад в общую поляризуемость молекул дают легко поляризуемые внешние (валентные) электроны, 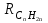 можно рассматривать и как сумму связевых рефракций: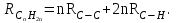 (28)Однако молекулярная рефракция изомерных нафтенов олефинов, содержащая очень легко поляризуемые π-связи, заметно больше. В системе атомных рефракций повышенный вклад С=С-связи учитывается добавлением постоянного слагаемого - инкремента двойной связи. 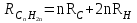 (29)В системе связевых рефракций сумма содержит иные слагаемые: 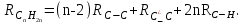 (30)Тройная углерод-углеродная связь имеет ещё бóльшую поляризуемость, чем двойная, и характеризуется бóльшими величинами инкремента молекулярной рефракции и связевой рефракции RС≡С, с помощью которых вычисляются рефракции ацетиленов: 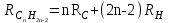 или 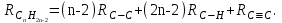 (31)Весьма важно, что изомерные ацетиленовые соединения с двумя двойными связями имеют иные (ещё больше) значения молекулярной рефракции, а именно - в системе атомных рефракций и инкрементов: 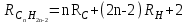 или в системе связевых рефракций: 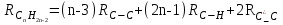 .(32)При этом только диены с изолированными и кумулированными (алленовыми  двойными связями обнаруживают согласие с расчётами по (7,9) или (7,10), а у диенов с сопряженными двойными связями  молекулярная рефракция оказывается большей, чем вычисленная по правилам аддитивности. Таким образом, открывается возможность определения по величинам молекулярной рефракции не только числа и природы содержащихся в молекуле (двойных и тройных) связей, но и их относительного расположения. Расхождение между экспериментальной и аддитивной (вычисленной с учётом инкрементов кратных связей) величинами R называется экзальтацией молекулярной рефракции ЕМ:ЕМ = R - Rадд. Главной причиной экзальтации является π-π-сопряжение простых связей, и величина экзальтации быстро возрастает с увеличением длины сопряженных систем. Однако частичное или полное включение сопряжённой системы в цикл, а также образование простейших ароматических структур приводит к снижению экзальтации, так что углеводороды ряда бензола и большинство их производных не обнаруживают экзальтации при расчёте аддитивных значений по формуле кекуле. Правилу аддитивости подчиняются не только ароматические соединения с несколькими изолированными бензольными кольцами, но соединения с конденсированными кольцами (нафталины, антрацены, фенантрены) и сопряженными (непосредственно соединенными) кольцами. Эти соединения так же проявляют эффект экзальтации. 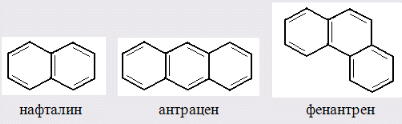 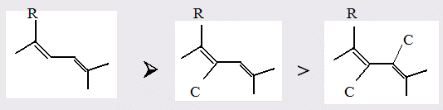 Для структурного анализа имеет значение также тот факт, что величина экзальтации существенно зависит от разветвлённости углеродного скелета в месте расположения сопряжённой системы: появление боковых цепей у центральных С-атомов сопряжённых связей влечёт за собой снижение экзальтации, так что в группах изомеров. В пределах одного гомологического ряда с данной сопряжённой системой экзальтация зачастую возрастает пропорционально массе. Для характеристики сопряжённых систем предлагалось использовать экзальтации, приведённые к молекулярной массе 100 а.е.м. - так называемые удельные экзальтации (Е∑): 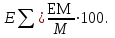 (33)р-π-сопряжение неподелённых электронных пар (галогенов, азота, кислорода) с π-электронами соседних кратных связей проявляется в разных структурах весьма различно. 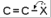 У непредельных галогенпроизводных эти эффекты столь невелики, что при расчётах по классической аддитивной схеме вообще не учитываются, а у галогенангидридов карбоновых кислот, RCOGal, амидов RCONH2 и ароматических аминов ArNH2 они по сложившейся традиции учитываются введением особых (повышенных) значений атомных или связевых рефракций галогенов и азота в таких структурах и, следовательно, формально не рассматриваются как экзальтации. Понятие "экзальтация рефракции" является, таким образом, весьма условным, связанным с примитивностью самой классической аддитивной схемы и её историей, но всё же полезным для выявления и классификации, содержащихся в исследуемом веществе сопряжённых систем. В современных, более детализированных аддитивных системах, учитывающих состояние гибридизации соседних атомов и влияние непосредственно не связанных атомов, понятие "экзальтация" вообще не используется. Однако такие схемы, разработанные для расчёта свойств органических соединений, требуют установления большого числа исходных аддитивных констант, предъявляют повышенные требования к чистоте исследуемых веществ и в повседневной практике структурного анализа не используются. Возможности структурного анализа по молекулярной рефракции, основанного на классической аддитивной схеме расчёта, ограничиваются информацией о числе и природе кратных связей и об эффектах сопряжения. В рамках выявления этих особенностей структуры обе разновидности классической аддитивной схемы (атомная и связевая) практически равноценны по точности и границам применимости. Более старая система атомных констант сохранила следы своего исторического развития: структурные эффекты учитываются в ней разными способами - различными значениями атомных рефракций данного элемента в разных группировках, специальными структурными инкрементами и групповыми рефракциями, используемыми наряду с атомными. Несмотря на разнородность расчетных констант, система атомных рефракций удобна при структурном анализе неизвестных веществ, так как позволяет производить вычисление Rадд, исходя непосредственно из брутто-формулы, без подсчёта числа различных связей в предположительных структурных формулах. |