рефрактометрия. Рефрактометрический метод анализа в химии
 Скачать 6.6 Mb. Скачать 6.6 Mb.
|
|
РЕФРАКТОМЕТРИЧЕСКИЙ МЕТОД АНАЛИЗА В ХИМИИ Оглавление Введение1. Некоторые понятия физической оптики 1.1 Распространение света .2 Показатель преломления света (показатель рефракции) 1.3 Дисперсия света 1.4 Полное внутреннее отражение 2. Дипольные моменты и рефракция 2.1 Поляризуемость и дипольный момент 2.1.1 Молярная поляризуемость 2.2 Молярная рефракция 3. Рефракция и структура молекул 3.1 Аддитивность рефракции 3.2 Оптическая экзальтация .3 Дисперсия молекулярной рефракции .4 Рефракция и размеры молекул 4. Рефрактометрия растворов 4.1 Анализ двухкомпонентных растворов 4.2 Анализ трёхкомпонентных растворов 5. Рефрактометрия полимеров Заключение Список используемой литературы Введение Рефрактометрический метод имеет многолетнюю историю применения в химии. Рефрактометрия (от латинского refraktus - преломлённый и греческого metréō - мерю, измеряю) - это раздел прикладной оптики, в котором рассматриваются методы измерения показателя преломления света (n) при переходе из одной фазы в другую, или, иными словами, показатель преломления n - это отношение скоростей света в граничащих средах. Применительно к химии рефракция имеет более широкое смысловое значение. Рефракция R (от латинского refractio - преломление) есть мера электронной поляризуемости атомов, молекул, ионов. Поляризация электронных облаков в молекулах отчётливо проявляется в инфракрасном (ИК) и ультрафиолетовом (УФ) поглощении веществ, но в ещё большей степени она ответственна за явление, которое количественно характеризуется молекулярной рефракцией. Когда свет как электромагнитное излучение проходит через вещество, то даже в отсутствие прямого поглощения он может взаимодействовать с электронными облаками молекул или ионов, вызывая их поляризацию. Взаимодействие электромагнитных полей светового пучка и электронного поля атома приводит к изменению поляризации молекулы и скорости светового потока. По мере возрастания поляризуемости среды возрастает и n - показатель, величина которого связана с молекулярной рефракцией. Указанное явление используется наряду с методом дипольных моментов для изучения структуры и свойств неорганических, органических и элементоорганических соединений. Рефрактометрия широко применяется также для определения строения координационных соединений (комплексов молекулярного и хелатного типа), изучения водородной связи, идентификации химических соединений, количественного и структурного анализа, определения физико-химических параметров веществ. В производственной практике показатель преломления света n используется для контроля степени чистоты и качества веществ; в аналитических целях - для идентификации химических соединений и их количественного определения. Таким образом, рефрактометрия - это метод исследования веществ, основанный на определении показателя преломления (коэффициента рефракции) и некоторых его функций. Из функций n, используемых в химии, наибольшее значение имеют: функция Лоренца - Ленца, производная n по концентрации растворённых веществ (инкремент n) и дисперсионные формулы, включающие разности показателей преломления для двух длин волн. Инкременты n используют в жидкостной хроматографии и при определении молекулярной массы полимеров методом рассеяния света. Для рефрактометрического анализа растворов в широких диапазонах концентраций пользуются таблицами или эмпирическими формулами, важнейшие из которых (для растворов сахарозы, этилового спирта и др.) утверждаются международными соглашениями и лежат в основе построения шкал специализированных рефрактометров для анализа промышленной и сельскохозяйственной продукции. Разработаны способы анализа трехкомпонентных растворов, основанных на одновременном определении n и плотности или вязкости, либо на осуществлении химических превращений с измерением n исходных и конечных растворов; эти способы применяют при контроле нефтепродуктов, фармацевтических препаратов и др. Идентификация органических соединений, минералов, лекарственных веществ осуществляется по таблицам n, приводимым в справочных изданиях. Преимуществами рефрактометрического метода являются его простота и относительно невысокая стоимость приборов для определения коэффициента преломления света. 1. Некоторые понятия физической оптики .1 Распространение света рефракция поляризуемость преломление химический Первая гипотеза - эмиссионная или корпускулярная, утверждала, что свет представляет собой поток мельчайших частиц - корпускул, испускаемых нагретым светящимся телом. Достигая глаза, эти частицы отражают зрительные ощущения. Ударяясь о преграду, частицы отражаются от её поверхности или проникают внутрь в зависимости от свойств материала тела. Легко объясняя законы отражения света, эта гипотеза не могла объяснить некоторые особенности преломления света и вовсе не объясняла интерференцию света. Вторая гипотеза - волновая, утверждала, что частицы, испускаемые светящимся телом, находятся в состоянии чрезвычайно быстрых колебаний, генерирующих волны, которые распространяются во все стороны и, достигая глаза, вызывают зрительные ощущения. Волновая теория хорошо объясняла интерференцию света и другие явления, недоступные корпускулярной гипотезе, но была не в состоянии объяснить, каким образом распространяются волны в вакууме. Впоследствии эта неясность была устранена признанием за световыми волнами электромагнитного характера. Таким образом, свет по этой гипотезе представляет собой быстро меняющееся электромагнитное поле. В дальнейшем с накоплением экспериментальных данных и их теоретической интерпретации, удалось установить особый, двойственный, характер световых явлений и свести обе, казалось, взаимоисключающие гипотезы в одну стройную, свободную от внутренних противоречий теорию. В соответствии с этой теорией свет равноправно может рассматриваться и как волновое движение электромагнитной природы, и как поток частиц, излучаемых источником света в виде отдельных порций света - квантов или фотонов. Вместе с тем световые явления могут рассматриваться также и с позиции геометрической или лучевой оптики, представляющей собой применение геометрических построений и теорем. Фундаментом для сближения геометрии с учением о свете и развития лучевой оптики явились представления о прямолинейности распространения света. Лучевая оптика и в настоящее время сохраняет ведущую роль во всех оптических и светотехнических расчётах, благодаря их простоте и наглядности, и показывает обычно полное соответствие вычисленных и экспериментальных данных. Лучевая оптика базируется на трёх основных приложениях: - прямолинейности распространения света в однородной среде; - поведении света на границе раздела двух сред при условии, что такая граница представляет собой идеально гладкую поверхность; - независимости распространения света. Указанные положения установлены эмпирически, т. е. опытным путём посредством сравнения геометрических соотношений без учёта особенностей, связанных со сложной природой света. Чтобы оперировать только наглядными геометрическими элементами, в лучевой оптике введены два условных понятия о луче и о светящейся точке. Под лучом понимают направление, по которому распространяется свет. Экспериментально установлено, что в вакууме и в однородной (газовой, жидкой или твёрдой) прозрачной среде (например, в воздухе при постоянном давлении, в воде или стекле) свет распространяется прямолинейно, и луч представляет собой прямую линию, началом которой является источник света. Под светящейся точкой понимают источник света, незначительными размерами которого можно пренебречь. Физически любой источник света обладает определёнными размерами, однако, если сравнить эти размеры с теми расстояниями, на которые распространяется действие света, то условно (без существенной погрешности) источник света принимают за точку. От светящейся точки света расходится во все стороны в виде пучка бесконечное число лучей, заполняющих всё окружающее пространство. Такой пучок называется неограниченным. Однако, если на пути такого пучка поместить диафрагму - непрозрачный экран с отверстием, то за диафрагмой свет будет распространяться уже как ограниченный пучок. Уменьшая отверстие диафрагмы, можно выделять всё более и более тонкие пучки. Казалось бы, это должно привести к столь тонкому пучку, что его можно считать "отдельным лучом". Однако опыт не подтверждает это предположение. При уменьшении диаметра отверстия лучи теряют прямолинейность и начинают огибать его края, и тем больше, чем меньше становится отверстие. Явление огибания световыми (звуковыми и т. д.) волнами встречающихся на пути препятствий называется дифракцией света и обусловлено его волновой природой. По этой причине нельзя выделить отдельный луч и в действительности существуют только пучки лучей. .2 Показатель преломления света (показатель рефракции) Если на пути светового пучка, распространяющегося в прозрачной однородной среде (например, в воздухе), встречается другая прозрачная однородная среда (например, стекло), то на границе раздела сред пучок света разделяется на два луча, из которых один луч входит в новую среду, изменяя своё направление (преломляется), а другой, отражаясь от поверхности раздела и изменяя своё направление, продолжает распространяться в первой среде. Луч при распространении в однородных средах, изменяя свою однонаправленность, сохраняет прямолинейность распространения и до, и после границы раздела (рис.1). Таким образом, преломление и отражение не противоречат прямолинейности распространения света в однородных средах. 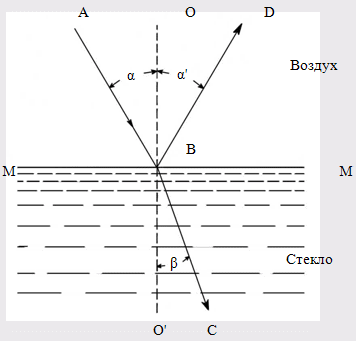 Рис. 1. Поведение луча на поверхности разделаЛиния ММ на рис. 1 изображает поверхность (границу) раздела между воздухом и стеклом. Падающий луч монохроматического света (света, условно одной длины волны) составляет с нормалью О\О’ к поверхности раздела сред угол АВО = α. Этот угол называется углом падения луча. В другой среде луч составляет с нормалью угол преломления О’ВС = β. Если изменять угол падения луча α, то будет изменяться и угол преломления луча β, но при этом всегда будет сохраняться неизменным отношение синуса угла падения луча к синусу угла преломления: 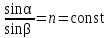 (1) (1)Если заменять стекло на другие однородные прозрачные среды (например, воду, другой сорт стекла), то в любом случае n будет оставаться величиной постоянной, но значения её будут другими. Причём, чем больше значение n, тем больше оптическая плотность второй среды. Если луч входит в какую-либо однородную прозрачную среду не из другой прозрачной среды, а из вакуума, то такой показатель преломления называется абсолютным показателем преломления среды (N). Поскольку значение n зависит от длины волны света (λ) и от температуры, то её измерение проводят при монохроматическом свете и постоянной температуре. Законы преломления света формулируются следующим образом: - падающий и преломлённый лучи находятся в одной плоскости с нормалью к поверхности раздела, но расположены на противоположных сторонах от неё; - отношение синуса угла падения луча к синусу угла преломления для двух соприкасающихся однородных сред постоянно и не зависит от угла падения; - падающий и преломленный лучи взаимно обратимы, т.е., если луч, входя из одной среды в другую, идет по направлению АВС, то, выходя из второй среды в первую, он пойдет по направлению СВА. Очевидно, при переходе из более плотной среды (стекло, рис. 1) в менее плотную (воздух) луч удалится от нормали, а показатель преломления примет обратное соотношение:  (2) (2)Показатель преломления как постоянная величина является характеристикой вещества (подобно температуре плавления). Свет как электромагнитное излучение при прохождении через однородную прозрачную среду, и взаимодействуя с её частицами (молекулами, атомами, ионами), изменяет свою скорость. Наибольшая скорость распространения света достигается в вакууме ( С0 = 3·1010 м/с). В воздухе скорость света (Св) уменьшается, и значение абсолютного показателя преломления воздуха (Nв) составляет: 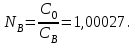 (3) (3)Относительный показатель преломления определённой среды nс - это отношение скорости света в воздухе к скорости света в исследуемой среде (Сс):  (4) (4)Таким образом, абсолютный и относительный показатели преломления воздуха связаны между собой соотношением: 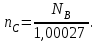 (5) (5)Для жидких и твердых тел n определяют, как правило, относительно воздуха, а для газов - относительно вакуума. .3 Дисперсия света В то время как для любого монохроматического луча углы падения равны углам отражения, показатель преломления в одной и той же среде разный для каждой длины волны λ. Поэтому, если на поверхность раздела сред будет падать не монохроматический, а "белый" свет, то после преломления отдельные его составляющие будут отклоняться по-разному и иметь разные углы преломления при одном и том же угле падения. Наибольшее отклонение происходит у самых коротковолновых (фиолетовых) лучей, а наименьшее - у самых длинноволновых (красных) лучей, т. е. "белый" свет, переходя в более плотную прозрачную однородную среду, рассеивается или диспергирует. Причиной дисперсии света является неодинаковая скорость распространения электромагнитного излучения различных длин волн в прозрачной однородной среде. Мерой дисперсии света служит разность между значениями показателя преломления, измеренным при различных длинах волн (например, ΔnFC; табл.1). Показатель преломления в зависимости от условий его определения дополняется латинской буковой n с подстрочным и надстрочным индексами (напрмер, 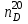 , , ). Верхний индекс показывает температуру (в 0С), а нижний индекс - линии или длину волны (в нм), при которых производилось измерение. Обычно n определяют при указанных в табл. 1 длинах волн. ). Верхний индекс показывает температуру (в 0С), а нижний индекс - линии или длину волны (в нм), при которых производилось измерение. Обычно n определяют при указанных в табл. 1 длинах волн.Обозначение показателя преломления от условий его определения Таблица 1
В рефрактометрии часто используется показатель n∞, значение которого определяют экстраполяцией зависимости n = f(λ) до бесконечно больших длин волн. Такая экстраполяция осуществляется обычно по формуле Коши: n = n∞ + b/λ. (6) Константы n∞ и b определяют, измерив n при разных λ (например λF и λС - линий спектра водорода). В большинстве случаев определяют не n∞, а nD желтой линии спектра натрия (D-линии). На практике используются три способа выражения дисперсии света. 1. Средняя дисперсия: ΔnFC = (nF − nC)∙104. (7) 2. Коэффициент дисперсии или число Аббе: 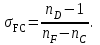 (8) (8)3. Удельная дисперсия:  (9) (9)где ρ - плотность вещества. Средняя дисперсия, nF - nC, частные дисперсии  и число Аббе служат важнейшими характеристиками оптических материалов. Относительная дисперсия и число Аббе служат важнейшими характеристиками оптических материалов. Относительная дисперсия 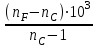 и родственные ей функции применяют для групповой идентификации углеводородов и анализа нефтяных фракций. и родственные ей функции применяют для групповой идентификации углеводородов и анализа нефтяных фракций.Поскольку показатель преломления изменяется с изменением температуры и длины волны света (который, безусловно, не должен поглощаться веществом), то первое условие должно быть, строго говоря, оговорено, но на самом деле изменение величины R в зависимости от температуры вполне укладывается в рамки ошибок эксперимента, и поэтому температуру указывать не обязательно. Наиболее часто используемыми длинами волн являются Нα-линии при 653,3 нм, Нβ-линия при 486,1 нм и D-линия натрия на 589,3, и значения R вполне чётко зависят от того, какая линия выбрана. Если нужно определить молекулярную рефракцию твёрдого вещества, то прибегают к модифицированному уравнению, учитывающему изменение показателя преломления с концентрацией раствора. 1.4 Полное внутреннее отражение 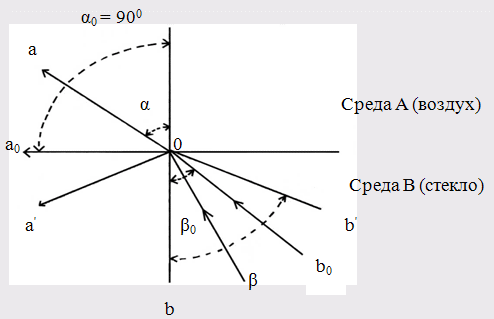 Рис.2. Схема направления распространения лучей при полном внутреннем отраженииb0Oa0 - распространение луча при предельном угле; b′Oa′ - распространение лучей при полном внутреннем отражении Если луч света распространяется из более плотной среды В в менее плотную среду А (рис.2), то при некотором угле β = β0 угол преломления α достигнет максимального значения α0 = 900. Далее луч будет распростра-няться вдоль поверхности раздела сред и выражение (2) примет следующий вид:  . . Если направить луч в среду В (рис. 2) под углом β > β0, то он вообще не попадёт в среду А, отразившись от поверхности раздела (рис. 2). Это явление называется полным внутренним отражением, а угол β0 - предельным углом. На измерении предельного угла основан принцип работы рефрактометров. 2. Дипольные моменты и рефракция Коэффициент преломления, как уже отмечалось, зависит от поляризуемости атомов, молекул и ионов. Поэтому исследование электрических характеристик вещества даёт важную информацию о распределении зарядов в молекуле и позволяет установить некоторые свойства вещества, обусловленные его электрической асимметрией. Рассмотрим некоторые вопросы, касающиеся природы возникновения дипольного момента в молекуле. .1 Поляризуемость и дипольный момент Любая молекула представляет собой совокупность положительно заряженных ядер и отрицательно заряженных электронов. При суммарном заряде, равном +е, заряд всех электронов будет равен -е . Если распределение ядер и электронов в пространстве таково, что центры "тяжести" положительных и отрицательных зарядов не совпадают, то молекула обладает постоянным дипольным моментом: μ =е∙l, (10) где l - расстояние между центрами электрических зарядов. Такая молекула является полярной. Мерой полярности молекулы служит величина дипольного момента, которую выражают в дебаях (D): D = 3,33564·10−30 Кл·м Дипольный момент - величина векторная. Направление вектора "→"выбирается от отрицательного полюса к положительному. В химической литературе, однако, традиционно принимается противоположное направление, т. е. от "+" к "−". Если в двухатомных молекулах простых веществ, т. е. состоящих из одинаковых атомов, и в многоатомных молекулах сложных веществ, обладающих высокой симметрией, центры "тяжести" разноимённых электрических зарядов совпадают (l = 0), то такие молекулы не обладают постоянным моментом (μ = 0) и являются неполярными. Если любую неполярную молекулу поместить в постоянное электрическое поле, создаваемое, например, конденсатором, то происходит её поляризация, выражающаяся в разнонаправленном смещении зарядов (деформационная поляризация). Тяжёлые ядра атомов будут несколько смещаться в сторону отрицательного полюса, а электроны незначительной массой будут легко смещаться в сторону положительного полюса. В результате центры "тяжести" положительных и отрицательных зарядов совпадать не будут, и в молекуле будет возникать индуцированный (наведённый) диполь, момент которого пропорционален напряжённости электрического поля: μинд = αD∙Е, (11) где Е - напряжённость внутреннего электрического поля в молекуле [эл. ст. ед./см2; Кл/см2] αD - коэффициент пропорциональности, который показывает, какой дипольный момент создается при напряжённости электрического поля равной единице. Чем больше αD, тем легче поляризуется молекула. Коэффициент αD, называемый деформационной поляризуемостью, равен сумме электронной αD и атомной поляризуемостей αат: αD = αэл + αат (12) Чем дальше удалены внешние (более подвижные) валентные электроны от атомных ядер, тем выше электронная поляризуемость молекулы. Так как смещение атомных ядер незначительно (αат составляет 5 - 10 % от αэл ) и им можно пренебречь, то приближённо будет αD = αэл. Таким образом, в электрическом поле образуется диполь с наведённым или как его называют индуцированным дипольным моментом. Если любую полярную молекулу поместить в электрическое поле, то будут происходить два процесса. Во-первых, молекула будет ориентироваться вдоль поля, и, во-вторых, расстояние между центрами "тяжести зарядов будет увеличиваться, увеличивая дипольный момент молекулы". Таким образом, полярные молекулы в электрическом поле так же, как и неполярные испытывают деформационную поляризацию. Кроме того, под влиянием электрического поля они ориентируются вдоль его силовых линий, стремясь принять устойчивое положение, отвечающее минимуму потенциальной энергии. Это явление, называемое ориентационной поляризацией, даёт эффект, эквивалентный увеличению поляризуемости молекулы на величину αор, называемую ориентационной поляризуемостью: 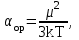 (13) (13)где k - постоянная Больцмана (1,380662(44)∙10−23 Дж/К); Т - абсолютная температура, К. Таким образом, полная поляризуемость молекулы α складывается из трёх величин: α = αэл + αат + αор или α = αD + αор (14) Из уравнений (11) и (12) следует, что полная поляризуемость α будет иметь размерность объёма [см3 или Å3]. .1.1 Молярная поляризуемость В электрическом (электромагнитном) поле молекулы поляризуются и возникает состояние напряжённости, характеризуемое величиной диэлектрической проницаемости (ε) вещества, которая входит в уравнение закона Кулона и может быть определена экспериментально. Измеряя диэлектрическую проницаемость, характеризующую вещество в целом, можно определить по теории поляризации диэлектриков электрооптические параметры его молекул, связанные с ε формулой Клаузиуса-Моссотти:  , (15) , (15)где NA - число Авогадро; М - молекулярная масса вещества; Ρ - плотность вещества, г/мл. РМ - молярная поляризация - величина, характеризующая меру индуцированного момента в объёме, который занимает 1 моль вещества. Молярная поляризация, дипольный момент и общая поляризуемость молекулы связаны друг с другом уравнением Дебая, которое выводится из уравнений (12) - (14): 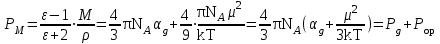 (16) (16)По уравнению Дебая можно вычислить значения α и μ по известным величинам ε, М и ρ. Поляризация молекул веществ, имеющих сравнительно большие значения ε и Р (например Н2О, HCN, HCl), зависит от температуры, уменьшаясь при её повышении. Молекулы таких веществ, не имея центра симметрии зарядов, являются постоянными диполями. Для них молярная поляризация в уравнении Дебая выражается линейной функцией от 1/Т: 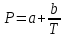 , (17) , (17)Где  и и 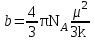 . .Вещества с μ = 0 состоят из симметричных молекул (например О2, СО2, СS2, молекулы многих углеводородов). В электрическом поле в таких молекулах возникает индуцированный дипольный момент. Поляризация молекул этого типа не зависит от температуры (рис. 3). Для случая молекул постоянных диполей (прямая а; рис. 3) отрезок ординаты ОА = а определяет величину поляризуемости α, а tgβ = b - величину дипольного момента μ Полная поляризация молекул может наблюдаться или в статическом электрическом поле, или в электромагнитном поле низкой частоты, но не в поле высокой частоты, где диполи не успевают ориентироваться. Поэтому, например, в поле низкочастотного инфракрасного излучения происходит и электронная, и атомная поляризация, а в более высокочастотном поле видимого света - только электронная поляризация (Рэл = 4/3πNАαэл), т.к. при высокочастотных колебаниях успевают смещаться только очень лёгкие частицы - электроны. Для неполярных веществ: РОР = 0 и Р = РД ≈ РЭЛ.  |
