Эконометрика. эконометрика. Регрессии нелинейные относительно включенных в анализ объясняющих переменных
 Скачать 26.01 Kb. Скачать 26.01 Kb.
|
|
Регрессии нелинейные относительно включенных в анализ объясняющих переменных. Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций: например, равносторонней гиперболы: 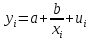 ; параболы второй степени: ; параболы второй степени: 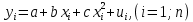 и др. и др.Различают два класса нелинейных регрессий: Регрессии, нелинейные относительно включенных в анализ объясняющих переменных (факторов), но линейные по оцениваемым параметрам; Регрессии, нелинейные по оцениваемым параметрам. Нелинейные регрессии по объясняющим переменным (факторам), но линейные по оцениваемым параметрам. Данный класс нелинейных регрессий включает уравнения, в которых результирующая переменная - 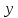 линейно связана с параметрами, но нелинейно связана с объясняющими переменными. Примером могут служить следующие функции: линейно связана с параметрами, но нелинейно связана с объясняющими переменными. Примером могут служить следующие функции:Полиномы разных степеней – 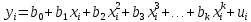 (полином (полином 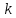 -ой степени); -ой степени);Равносторонняя гипербола – 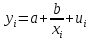 . .Оценка параметров регрессий нелинейных по объясняющим переменным. При этом используется подход, именуемый «замена переменных». Суть его состоит в замене «нелинейных» объясняющих переменных новыми «линейными» переменными и сведение нелинейной регрессии к линейной. К новой «преобразованной» регрессии может быть применен обычный метод наименьших квадратов (МНК). Рассмотрим применение данного подхода к параболе второй степени: 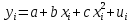 . Заменяя переменную . Заменяя переменную 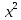 на на 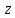 получим двухфакторное уравнение линейной регрессии: получим двухфакторное уравнение линейной регрессии: 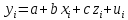 , для оценки параметров которого используется обычный МНК. , для оценки параметров которого используется обычный МНК.Соответственно, для полинома k-ого порядка: 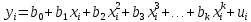 , при замене: , при замене: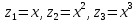 , ..., , ..., 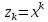 , получим: , получим: 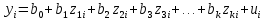 . .Среди нелинейной полиноминальной регрессии чаще всего используется парабола второй степени; в отдельных случаях – полином третьего порядка. Ограничение в использовании полиномов более высоких степеней связаны с требованием однородности исследуемой совокупности: чем выше порядок полинома, тем больше изгибов имеет кривая и соответственно менее однородна совокупность по результативному признаку. Парабола второй степени целесообразна к применению, если для определенного интервала значений фактора меняется характер связи с результатом: прямая связь меняется на обратную или обратная на прямую. В этом случае определяется значение фактора, при котором достигается максимальное (или минимальное) значение результативного признака: Если же исходные данные не обнаруживают изменения направленности связи, то параметры параболы второй степени становятся трудно интерпретируемыми, а форма связи часто заменяется другими нелинейными моделями. Рассмотрим, как оценивают параметры в случае равносторонней гиперболы: 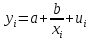 . Для этого заменим . Для этого заменим 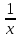 на на 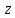 , получим линейное уравнение регрессии: , получим линейное уравнение регрессии: 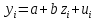 , параметры которого оценивают обычным МНК. , параметры которого оценивают обычным МНК.Равносторонняя регрессия может быть использована, например, для характеристики связи удельных расходов сырья, материалов и топлива с объемом выпускаемой продукции. При 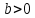 имеем обратную зависимость, которая при имеем обратную зависимость, которая при 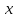 характеризуется нижней асимптотой, т.е. минимальным предельным значением характеризуется нижней асимптотой, т.е. минимальным предельным значением 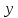 , оценкой которого служит параметр , оценкой которого служит параметр 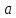 . При . При 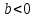 имеем медленно повышающуюся функцию с верхней асимптотой при имеем медленно повышающуюся функцию с верхней асимптотой при 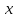 , т.е. максимальным предельным уровнемy, оценкой которого служит параметр , т.е. максимальным предельным уровнемy, оценкой которого служит параметр 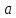 . .Структурная и приведенная формы модели. Система совместных, одновременных уравнений (или структурная форма модели) обычно содержит эндогенные и экзогенные переменные. Эндогенные переменные – это зависимые переменные, число которых равно числу уравнений в системе и которые обозначаются через 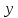 . Экзогенные переменные – это предопределенные переменные, влияющие на эндогенные переменные, но не зависящие от них. Обозначаются через . Экзогенные переменные – это предопределенные переменные, влияющие на эндогенные переменные, но не зависящие от них. Обозначаются через 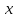 . .Классификация переменных на эндогенные и экзогенные зависит от теоретической концепции принятой модели. Экономические переменные могут выступать в одних моделях как эндогенные, а в других как экзогенные переменные. Внеэкономические переменные (например, климатические условия, социальное положение, пол, возрастная категория) входят в систему только как экзогенные переменные. В качестве экзогенных переменных могут рассматриваться значения эндогенных переменных за предшествующий период времени (лаговые переменные). Структурная форма модели позволяет увидеть влияние изменений любой экзогенной переменной на значения эндогенной переменной. Целесообразно в качестве экзогенных переменных выбирать такие переменные, которые могут быть объектом регулирования. Меняя их и управляя ими, можно заранее иметь целевые значения эндогенных переменных. Структурная форма модели в правой части содержит при эндогенных переменных коэффициенты 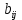 и экзогенных переменных – коэффициенты и экзогенных переменных – коэффициенты 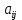 , которые называются структурными коэффициентами модели. Все переменные в модели выражены в отклонениях от среднего уровня, т. е. под , которые называются структурными коэффициентами модели. Все переменные в модели выражены в отклонениях от среднего уровня, т. е. под 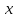 подразумевается подразумевается 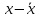 , а под , а под 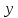 – соответственно – соответственно 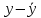 . Поэтому свободный член в каждом уравнении системы отсутствует. . Поэтому свободный член в каждом уравнении системы отсутствует.Использование МНК для оценивания структурных коэффициентов модели дает, как принято считать в теории, смещенные и несостоятельные оценки. Поэтому обычно для определения структурных коэффициентов модели структурная форма модели преобразуется в приведенную форму модели. Приведенная форма модели представляет собой систему линейных функций эндогенных переменных от экзогенных: 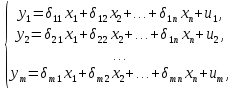 Где 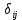 – коэффициенты приведенной формы модели, – коэффициенты приведенной формы модели,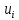 – остаточная величина для приведенной формы. – остаточная величина для приведенной формы.По своему виду приведенная форма модели ничем не отличается от системы независимых уравнений, параметры которой оцениваются традиционным МНК. Применяя МНК, можно оценить 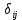 , а затем оценить значения эндогенных переменных через экзогенные. , а затем оценить значения эндогенных переменных через экзогенные.Коэффициенты приведенной формы модели представляют собой нелинейные функции коэффициентов структурной формы модели. Рассмотрим это положение на примере простейшей структурной модели, выразив коэффициенты приведенной формы модели через коэффициенты структурной модели. Для структурной модели вида 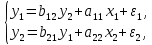 (*) (*)Приведенная форма модели имеет вид 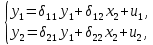 (**) (**)Из первого уравнения (*) можно выразить 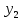 следующим образом (ради упрощения опускаем случайную величину): следующим образом (ради упрощения опускаем случайную величину):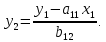 Подставляя во второе уравнение (*), имеем 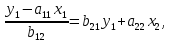 Откуда 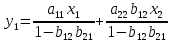 . .Поступая аналогично со вторым уравнением системы (*), получим 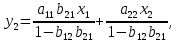 Т. е. система (*) принимает вид 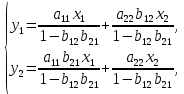 Таким образом, можно сделать вывод о том, что коэффициенты приведенной формы (**) модели будут выражаться через коэффициенты структурной формы следующим образом: 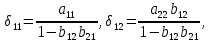 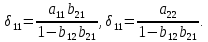 Следует заметить, что приведенная форма модели хотя и позволяет получить значения эндогенной переменной через значения экзогенных переменных, но аналитически она уступает структурной форме модели, так как в ней отсутствуют оценки взаимосвязи между эндогенными переменными. При переходе от приведенной формы модели к структурной эконометрист сталкивается с проблемой идентификации. Идентификация – это единственность соответствия между приведенной и структурной формами модели. Структурная модель в полном виде содержит 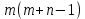 параметров, а приведенная форма модели в полном виде содержит параметров, а приведенная форма модели в полном виде содержит 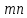 параметров. Т. е. в полном виде структурная модель содержит большее число параметров, чем приведенная форма модели. Соответственно параметров. Т. е. в полном виде структурная модель содержит большее число параметров, чем приведенная форма модели. Соответственно 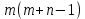 параметров структурной модели не могут быть однозначно определены из параметров структурной модели не могут быть однозначно определены из 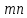 параметров приведенной формы модели. параметров приведенной формы модели.Чтобы получить единственно возможное решение для структурной модели, необходимо предположить, что некоторые из структурных коэффициентов модели ввиду слабой взаимосвязи признаков с эндогенной переменной из левой части системы равны нулю. Тем самым уменьшится число структурных коэффициентов модели. Уменьшение числа структурных коэффициентов модели возможно и другим путем: например, путем приравнивания некоторых коэффициентов друг к другу, т. е. путем предположений, что их воздействие на формируемую эндогенную переменную одинаково. На структурные коэффициенты могут накладываться, например, ограничения вида 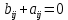 . .С позиции идентифицируемости структурные модели можно подразделить на три вида: 1) идентифицируемые; 2) неидентифицируемые; 3) сверхидентифицируемые. Модель Идентифицируема, если все структурные ее коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной формы модели, т. е. если число параметров структурной модели равно числу параметров приведенной формы модели. В этом случае структурные коэффициенты модели оцениваются через параметры приведенной формы модели и модель идентифицируема. Модель Неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов, и в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели. Модель Сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае на основе коэффициентов приведенной формы можно получить два или более значений одного структурного коэффициента. В этой модели число структурных коэффициентов меньше числа коэффициентов приведенной формы. Сверхидентифицируемая модель в отличие от неидентифицируемой модели практически решаема, но требует для этого специальных методов исчисления параметров. Структурная модель всегда представляет собой систему совместных уравнений, каждое из которых требуется проверять на идентификацию. Модель считается идентифицируемой, если каждое уравнение системы идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель считается неидентифицируемой. Сверхидентифицируемая модель содержит хотя бы одно сверхидентифицируемое уравнение. |
