теплоотдача. Рекуперативные теплообменные аппараты
 Скачать 3.22 Mb. Скачать 3.22 Mb.
|
2. Общие принципы расчета теплообменных аппаратов2.1 Конструктивный расчеттеп лообменных аппаратовКонструкции теплообменных аппаратов весьма разнообразны, однако существует общая методика теплотехнических расчетов, которую можно применить для частных расчетов в зависимости от имеющихся исходных данных. Существуют два вида теплового расчета: конструктивный (проектный) и поверочный. Конструктивный расчет выполняется при проектировании теплообменного аппарата, когда заданы теплопроизводительность аппарата, теплоносители, их расходы и параметры. Целью такого расчета является определение поверхности теплообмена и конструктивных размеров выбранного типа аппарата. Конструктивный расчет состоит из теплового(теплотехнического), гидравлического и механического расчетов. Цель теплового расчета определить требуемую поверхность теплообмена и подобрать стандартизованный аппарат. Расчет теплообменника состоит из двух этапов: предварительный (ориентировочный) тепловой расчет, в рамках которого определяют ориентировочную поверхность теплообмена и предварительно принимают аппарат; уточненный тепловой расчет проводится с целью уточнения поверхности теплообмена путем расчета параметров, характеризующих процесс теплообмена – коэффициентов теплоотдачи и теплопередачи с учетом режимов движения потоков в предварительно выбранном аппарате. Гидравлический расчет проводится с целью определения достаточности давления, создаваемого насосами (компрессорами) для преодоления сопротивлений, возникающих при движении потока через аппарат. В механическом расчете аппарата обоснованно выбирают материалы для изготовления элементов конструкции и проводят все необходимые прочностные расчеты, подтверждающие возможность его безопасной и длительной эксплуатации при заданных параметрах работы (температура, давление) и с учетом свойств теплообменивающихся потоков. Для выполнения конструктивного расчета необходимы следующие исходные данные: тип теплообменного аппарата (кожухотрубчатый, пластинчатый, ребристый, оросительный, погружной илидр.); теплоносители (газ, пар или жидкость); теплопроизводительность аппарата: расход одного из теплоносителей и его начальная и конечная температуры. По ходу выполнения расчета определяют: физические параметры и скорости движения теплоносителей; расход другого теплоносителя из уравнения тепловогобаланса; среднююразностьтемператур; коэффициентытеплоотдачиитеплопередачи; поверхностьтеплообмена; конструктивныеразмерыаппарата; диаметр патрубка для входа и выходатеплоносителей. 2.1.1 Определение физических параметров и скоростей движениятеплоносителейТеплообмен между теплоносителями существенно изменяется в зависимости от физических свойств и параметров движущихся сред, а также от гидродинамических условий движения. Физические параметры теплоносителей зависят от температуры и определяются по справочной литературе в зависимости от выбранной средней температуры среды. Средняя температура среды tcp, °С, приближенно определяется как сред- нее арифметическое начальной tн и конечной tк температур: tср 0,5tн tк . Основными физическими параметрами рабочих сред являются плотность, вязкость, теплоемкость, теплопроводность, температура кипения, скрытая теплота испарения или конденсации и др. При конструировании теплообменной аппаратуры обычно выбирают та- кие скорости теплоносителей, при которых коэффициенты теплоотдачи и гидравлические сопротивления были бы экономическивыгодными. Выбор оптимальной скорости имеет большое значение для качественной работы теплообменного аппарата, так как увеличение скоростей теплоносителей приводит к интенсификации теплообмена (возрастают коэффициенты теплопередачи) и уменьшению поверхности нагрева, т. е. аппарат становится компактнее, однако при этом значительно возрастают гидравлические сопротивления и, естественно, увеличивается расход электроэнергии на перекачку, а также появляется опасность гидравлического удара и вибрации труб. По- этому часто бывает необходимо произвести технико-экономический расчет для выбора наивыгоднейших скоростей теплоносителей. Обычно минималь-ное значение скорости теплоносителя выбирается соответствующим началу турбулентного движения потока, т. е. числу Рейнольдса больше 104. Для наиболее часто применяемых диаметров труб (57, 38 и 25 мм) рекомендуются скорости жидкости 1,5…3 м/с; низший предел скорости для большинства жидкостей составляет 0,06…0,3 м/с. Для маловязких жидкостей скорость, соответствующая Re = 104, не превышает 0,2…0,3 м/с. Для вязких жидкостей турбулентность потока достигается при значительно больших скоростях, поэтому при расчетах приходится допускать переходный или да- же ламинарный режим. Для газов при атмосферном давлении допускаются скорости до 25 м/с, для насыщенных паров при конденсации рекомендуются скорости до 10м/с. Рекомендуемые скорости движения теплоносителей в патрубках по дан-ным [1] следующие: для жидкостей 1,5…3 м/с; для конденсата греющего пара 1…2 м/с; для насыщенного пара 20…30 м/с; для перегретого пара 25…60 м/с. 2.1.2 Тепловые балансы теплообменных аппаратовТепловой расчет начинается с определения тепловой нагрузки аппарата и расхода одного из теплоносителей. Тепловая нагрузка – количество теплоты, переданное от горячего теплоносителя к холодному. В зависимости от заданного процесса уравнения тепловых балансов имеют различный вид. Для подогревателей. Если нагрев одного из теплоносителей происходит за счет охлаждения другого теплоносителя, т. е. аппарат работает без изменения агрегатного (фазового) состояния теплоносителей, то уравнения теплового баланса имеют вид: 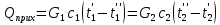 где G1 и G2 — массовые расходы теплоносителей (воздуха, газов и т. п.), не изменяющих агрегатного состояния; с1 и с2 — теплоемкости теплоносителей; 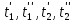 начальные и конечные температуры теплоносителей. начальные и конечные температуры теплоносителей.Уравнение теплового баланса с учетом потерь: 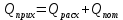 где Qпот — потери теплоты от стенок аппарата в окружающую среду. Из практики известно, что тепловые потери составляют обычно 2…3 % количества подведенной теплоты. Их можно учесть коэффициентом η =0,97…0,98 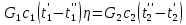 В этом случае расход греющего теплоносителя выразится как 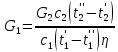 Для компактных конструкций величина тепловых потерь значительно меньше и не достигает 1 %. Тепловые потери изолированных теплообменников пропорциональны их наружной поверхности и ограничены предельно допустимой температурой. Если нагрев одного из теплоносителей происходит за счет конденсации греющего водяного насыщенного пара, то 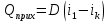 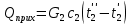 где D–количество греющего пара; i1–энтальпия греющего пара (определяется из прил. 2, табл. 1); iк–энтальпия конденсата, iк= cвiк; G2–масса (или массовый расход) нагреваемого вещества; с2– теплоемкость нагреваемого вещества; 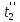 –конечная температура нагреваемого вещества; –конечная температура нагреваемого вещества; 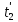 –начальная температура нагреваемого вещества. Расход греющего пара выразится из уравнения теплового баланса: –начальная температура нагреваемого вещества. Расход греющего пара выразится из уравнения теплового баланса: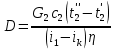 Для испарителей. Нагрев и охлаждение теплоносителей сопровождаются изменением их агрегатного состояния, например, насыщенный пар, нагревая воду до состояния кипения и последующего интенсивного испарения, сам конденсируется 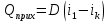 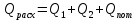 где Q1–теплота, израсходованная на нагрев холодного теплоносителя до температуры кипения; Q2–теплота, затраченная на испарение кипящей жидкости 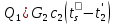 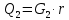 где G2–количество (или расход) холодного теплоносителя; с2–средняя теплоемкость теплоносителя; ts–температура кипения холодного теплоносителя; t2 – начальная температура холодного теплоносителя; r–скрытая теплота испарения теплоносителя. Тогда расход греющего пара 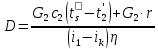 Для конденсаторов. Более нагретый теплоноситель охлаждается с изменением агрегатного состояния. Теплота от горячего теплоносителя чаще всего отводится холодной водой 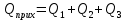 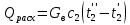 где Q1– теплота, выделяющаяся при охлаждении перегретых паров до насыщенного состояния; Q2– теплота, выделяющаяся при конденсации насыщенного пара; Q3– теплота, выделяющаяся при охлаждении горячей жидкости до заданной температуры; Gв – расход охлаждающей воды; 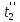 –конечная температура горячего теплоносителя; –конечная температура горячего теплоносителя; 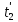 – начальная температура горячего теплоносителя – начальная температура горячего теплоносителя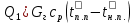 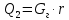 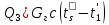 Q1 Gгсрtп.пtн.п; Q2 Gгr; Q3Gгсtst1, где Gг–количество горячего теплоносителя; ср–теплоемкость при постоянном давлении для перегретого пара; tп.п– температура перегретого пара; tн.п–температура насыщенного пара; r–скрытая теплота конденсации горя- чего теплоносителя; с –теплоемкость жидкого горячего теплоносителя; ts–температура кипения горячего теплоносителя. Если охлаждающая вода подается в межтрубное пространство и внешние стенки аппарата имеют температуру, мало отличающуюся от температуры окружающей среды, то тепловыми потерями вследствие их малости пренебрегают. Расход охлаждающей воды определяется из уравнения теплового баланса по формуле 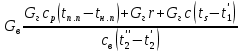 2.1.3 Определение среднего температурного напораСредний температурный напор зависит от схемы движения теплоносителей в теплообменнике и от соотношения водяных эквивалентов W, Вт/ºС, численная величина которых определяет собой количество воды, которое по теплоемкости пропорционально теплоемкости массового расхода рассматриваемого теплоносителя в единицу времени: 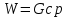 , ,где G— массовый расход теплоносителя; ср— теплоемкость теплоносителя. В зависимости от того, осуществляется ли прямоток или противоток и W1больше или меньше, чем W2, получаются четыре характерные парыкривыхизменениятемпературывдольповерхностинагрева,представленныенарис.1. 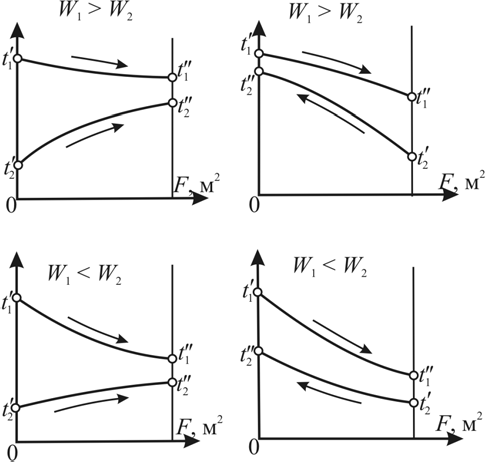 а б Рис. 12. Характер изменения температур теплоносителей при прямотоке (а) и противотоке (б) Из рис. 12 видно, что при прямотоке наибольшая разность температур будет всегда на входе в теплообменник, а наименьшая на выходе из него. В противоточной схеме место наибольшей и наименьшей разности температур заранее определить нельзя, оно зависит от соотношений водных эквивалентовW1<W2илиW1>W2.  Если температуры теплоносителей изменяются вдоль поверхности нагрева незначительно Если температуры теплоносителей изменяются вдоль поверхности нагрева незначительно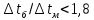 то средний температурный напор можно считать как средний арифметический то средний температурный напор можно считать как средний арифметический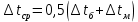 Во всех остальных случаях средний температурный напор следует считать как средний логарифмический 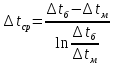 где Δtб и Δtм — большая и меньшая разности температур между первичными и вторичными теплоносителями на концах теплообменника. В теплообменных аппаратах противоток имеет ряд преимуществ по сравнению с прямотоком. Так при одних и тех же начальных и конечных температурах теплоносителей для противотока в большинстве практических случаев получается большая средняя разность температур, что позволяет иметь меньшую поверхность нагрева аппарата при той же производительности. Поэтому противоточную схему движения теплоносителей следует применять во всех случаях, когда этому не препятствует технология производства или другие обстоятельства. 2.1.4 Определение коэффициентов теплоотдачи и теплопередачиКоэффициент теплопередачи kпредставляет собой количественную расчетную величину, характеризующую сложный теплообмен. Он зависит от коэффициентов теплоотдачи, термического сопротивления стенки и загряз- нений. Для плоской стенки 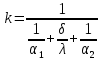 Для цилиндрической системы 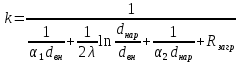 где δ — толщина стенки аппарата; Rзагр— термическое сопротивление, учитывающее загрязнение (накипь, сажа и пр.) с обеих сторон стенки, м2К/Вт; 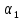 — коэффициент теплоотдачи от горячего теплоносителя; λ — коэффициент теплопроводности материала стенки; — коэффициент теплоотдачи от горячего теплоносителя; λ — коэффициент теплопроводности материала стенки; 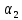 — коэффициент теплоотдачи от стенки к холодному теплоносителю. — коэффициент теплоотдачи от стенки к холодному теплоносителю.Если теплопроводность слоя загрязнения неизвестна, подсчитывают коэффициент теплопередачи kдля чистой стенки и вводят поправку на ее загрязнение при помощи коэффициента φиспользования поверхности теплообмена 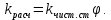 Для большинства аппаратов числовое значение коэффициента лежит в пределах φ = 0,65…0,85. Коэффициенты теплоотдачи со стороны горячего 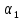 и со стороны холодного и со стороны холодного 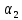 теплоносителей находят по эмпирическимкритериальным формулам, в зависимости от вида теплообмена (свободная или вынужденная конвекция, кипение, конденсация), характера течения (течение в трубах и каналах, продольное или поперечное обтекание трубных пучков и т.п.), режима течения (ламинарный, переходный, турбулентный), расположения поверхности нагрева (горизонтальное или вертикальное). теплоносителей находят по эмпирическимкритериальным формулам, в зависимости от вида теплообмена (свободная или вынужденная конвекция, кипение, конденсация), характера течения (течение в трубах и каналах, продольное или поперечное обтекание трубных пучков и т.п.), режима течения (ламинарный, переходный, турбулентный), расположения поверхности нагрева (горизонтальное или вертикальное).Алгоритм расчета коэффициента теплоотдачи по критериальным формулам для однофазных теплоносителей заключается в следующем. 1. Определяют вид конвективного теплообмена: свободная или вынужденная конвекция и объект, где она про- исходит и по литературе [2–7] выбирают критериальное уравнение соответствующее данному виду конвективного теплообмена. Основные критериальные уравнения приведены ниже в данном пособии. 2. Согласно требованиям, изложенным в комментариях к критериальным уравнениям, находят определяющие параметры: – определяющий размер; – определяющую температуру, по которой из справочных таблиц находят физические свойства текучей среды ( 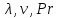 и т.д.); и т.д.);– при вынужденном движении скорость течения флюида. Если скорость теплоносителя неизвестна, то её рассчитывают из уравнения неразрывности (1.12). 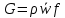 , ,где 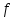 – площадь поперечного сечения канала, м2/с; – площадь поперечного сечения канала, м2/с;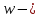 скорость теплоносителя м/с скорость теплоносителя м/с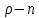 лотность теплоносителя ρ находят по справочнику[1] при средней температуре теплоносителя лотность теплоносителя ρ находят по справочнику[1] при средней температуре теплоносителя3. Определяют режим течения среды: – при вынужденном движении жидкости или газа по критерию Рейнольдса (Re); – при свободном движении флюида по критерию Рэлея (Ra). Уточняют вид критериальной формулы в зависимости от режима движения текучей среды. 4. По критериальному уравнению находят безразмерный коэффициент теплоотдачи – число Нуссельта (Nu). 5. Используя определение критерия Нуссельта, рассчитывают коэффициент конвективной теплоотдачи. В критериальные уравнения входят величины, зависящие от температур наружной и внутренней стенок Тw1 и Тw2, которые заранее неизвестны, поэтому Тw1 и Тw2 рассчитывают методом последовательных приближений. Первый алгоритм уточнения температур стенок Тw1 и Тw2 Задают неизвестные температуры стенок Тw1 и Тw2 в первом приближении: 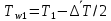 , ,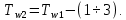 2. Коэффициент теплопроводности материала трубок λw находят по справочнику [1] при средней температуре стенки (Тw1 + Тw2)/2. 3. По критериальным уравнениям определяют коэффициенты теплоотдачи со стороны горячего и холодного теплоносителей α1 и α2. 4. Рассчитывают коэффициент теплопередачи k через стенку теплообменника. 5. Уточняют температуры стенок Тw1 и Тw2. Для этого рассчитывают плотность теплового потока через стенку между средними температурами Т1и Т2 теплоносителей: 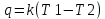 ,(1.34) ,(1.34)Тогда температуры стенок будут равны  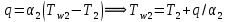 Если расхождение между полученными и заданными значениями температур стенок больше 5 %, то расчет повторяют с пункта 2 первого алгоритма для новых значений температур стенок Тw1 и Тw2. Второй алгоритм уточнения температурстенок Тw1 и Тw2 1. В первом приближении принимают коэффициентытеплоотдачи α1 и α2, используя следующие рекомендации [2,11,12]: нагрев и охлаждение газов 4 ÷ 50 Вт/(м2К), нагрев и охлаждение воды 500 ÷ 10000 Вт/(м2К), нагрев и охлаждение масел 50 ÷ 1000 Вт/(м2К), кипение воды 1000 ÷ 45000 Вт/(м2К), пленочная конденсация водяного пара 4000 ÷ 15000 Вт/(м2К). 2. Находят коэффициент теплопроводности материаластенкиλw по справочнику [1] при температуре стенки, которую в первом приближении считают равной (Т1 + Т2)/2,где Т1 и Т2 средние температуры теплоносителей. 3. Находят температуры стенок Тw1 и Тw2 по уравнениям: 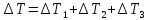 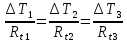 где 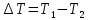 – перепад температур между горячим и холодным теплоносителями, 0С; – перепад температур между горячим и холодным теплоносителями, 0С; 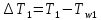 – перепад температур между горячим теплоносителем и стенкой, 0С; – перепад температур между горячим теплоносителем и стенкой, 0С;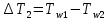 – перепад температур в стенке, 0С; – перепад температур в стенке, 0С;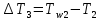 – перепад температур между стенкой и холодным теплоносителем, 0С; Rt1 = 1 /α1 – термическое сопротивление теплоотдачи от горячего теплоносителя к стенке, (м2·К)/Вт; Rt2 =δ/λ– термическое сопротивление теплопроводности стенки, (м2·К)/Вт; Rt3=1/α1 – термическое сопротивление теплоотдачи от стенки к холодному теплоносителю, (м2·К)/Вт; δ – толщина плоской стенки или δ = 0,5(dнар – dвн) – толщина стенки трубы, м. – перепад температур между стенкой и холодным теплоносителем, 0С; Rt1 = 1 /α1 – термическое сопротивление теплоотдачи от горячего теплоносителя к стенке, (м2·К)/Вт; Rt2 =δ/λ– термическое сопротивление теплопроводности стенки, (м2·К)/Вт; Rt3=1/α1 – термическое сопротивление теплоотдачи от стенки к холодному теплоносителю, (м2·К)/Вт; δ – толщина плоской стенки или δ = 0,5(dнар – dвн) – толщина стенки трубы, м.В результате совместного решения уравнений (1.37) и (1.38) получают 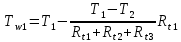 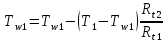 4. По критериальным уравнениям определяют коэффициенты теплоотдачи со стороны горячего α1 и со стороны холодного α2. теплоносителей. Если расхождение между полученным и заданным значениями коэффициентов теплоотдачи больше 5 %, то расчет повторяют с пункта 2 для новых значений α1 и α2. При выполнении конструктивного расчета скорости движения теплоносителей принимают в интервале 0,5 ÷ 3 м/с для жидкостей и 5 ÷ 20 м/с для газов. Если необходимо получить компактный теплообменник, то выбираюn более высокие скорости. Если размеры теплообменника не лимитированы, а эксплуатационные затраты на транспорт теплоносителей необходимо свести к минимуму, то выбирают скорости на левой границе рекомендуемого интервала. Оптимальное значение скоростей движения теплоносителей может быть получено при проведении технико-экономического расчета. При выполнении поверочного расчета скорости движения теплоносителей находят из уравнения неразрывности. Ниже приведены критериальные уравнения для расчета коэффициентов теплоотдачи в наиболее часто встречающихся случаях теплообмена [7]. Коэффициенты теплоотдачи 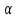 определяются в большинстве случаев из выражения для критерияНуссельта определяются в большинстве случаев из выражения для критерияНуссельта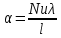 где Nu– безразмерный критерий подобия – критерий Нуссельта; λ – коэффициент теплопроводности того теплоносителя, для которого определяется коэффициент теплоотдачи; l – определяющий геометрический размер. Критерий Nu определяется в зависимости от характера движения и агрегатного состояния теплоносителей по критериальным уравнениям различного вида. Обобщение экспериментальных данных различных исследователей дает для расчета среднего коэффициента теплоотдачи следующие критериальные уравнения [5]: при турбулентном течении различных жидкостей внутри труб (кроме жидких металлов) для диапазона чисел Рейнольдса 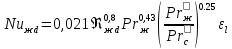 для ламинарного режима течения: При ламинарном режиме течения (Re 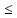 2300 ) возможны два случая: 2300 ) возможны два случая:а) При значениях числа Рэлея Ra< 8·105 влияние свободной конвекции можно не учитывать и коэффициент теплоотдачи для теплоносителя, движущегося в трубах круглого сечения, определяют по уравнению 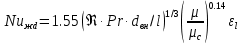 где 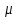 и и 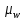 – динамический коэффициент вязкости текучей среды при средней температуре теплоносителя и при температуре стенки, Па·с. – динамический коэффициент вязкости текучей среды при средней температуре теплоносителя и при температуре стенки, Па·с. При значениях числа Рэлея Ra ≥ 8·105 наступает так называемый вязкостно-гравитационный режим, при котором влиянием свободной конвекции пренебречь нельзя. В этом режиме на теплоотдачу существенно влияет и вынужденное движение и свободная конвекция. Коэффициент теплоотдачи при вязкостно-гравитационном режиме течения находят по уравнению 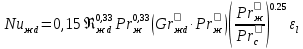 где Reжd –критерий Рейнольдса, определенный по температуре жидкости при определяющем размере трубы; Рrж–критерий Прандтля, определенный по температуре жидкости; Рrс–критерий Прантдля, определенный по температуре стенки; εl–коэффициент, учитывающий изменение среднего коэффициента теплоотдачи по длине трубы: при l/d≥ 50 εl= l, при l/d<50 необходимо учитывать влияние начального термического участка; значения εlв зависимости от числа Re и отношения l/dприведены в справочной литературе [3]. − При переходном режиме движения теплоносителей (2300 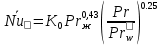 где комплекс K0 находят по табл. 1 в зависимости от числа Рейнольдса. Таблица 1- Зависимость комплекса К0 от числа Рейнольдса
При поперечном обтекании одиночных круглых труб и когда угол атаки ψ, составленный направлением движения потока жидкости и осью трубы, равен 90, средний по периметру коэффициент теплоотдачи определяется из соотношений[6]: при5 <Ref<103 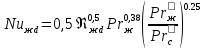 при 103 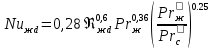 при 3·105 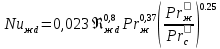 При поперечном обтекании коридорного пучка труб при Ref> 103 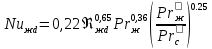 При поперечном обтекании шахматного пучка труб при Ref> 103 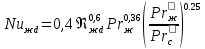 При течении среды в кольцевом канале между гладкими трубками: 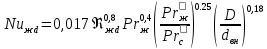 При пленочной конденсации насыщенного пара и ламинарном стекании пленки конденсата под действием силы тяжести коэффициент теплоотдачи рассчитывают по формуле [2,3]: 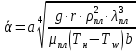 где a = 0,943, b = H – для вертикальной поверхности; a = 0,728, b = dнар – для горизонтальной трубы. Для горизонтальной трубы ламинарный режим течения пленки существует, если выполняется условие 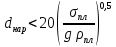 Физические свойства конденсата находят при температуре насыщения Тн. Формулы для расчета локальных коэффициентов теплоотдачи, теплоотдачи при волновом и турбулентном течении пленки, а также толщины конденсатной пленки приведены в литературе [2–5]. При пузырьковом кипении в большом объеме в условиях естественной конвекции (на внешней поверхности пучков труб) [2, 3, 6]: 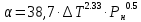 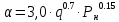 где Pн – давление насыщения, бар; q – плотность теплового потока, Вт/м2; 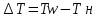 – перегрев жидкости в пограничном слое. – перегрев жидкости в пограничном слое.При пузырьковом кипении в трубах и каналах в условиях свободного или вынужденного движения [2] расчет коэффициента теплоотдачи выполняют по следующему алгоритму. а) Находят коэффициент теплоотдачи при кипении в большом объеме αкип б) Рассчитывают коэффициент теплоотдачи при вынужденном турбулентном течении в трубах и каналах αw по критериальному уравнению (1.41). При этом в качестве определяющей температуры необходимо принять температуру насыщения Тн при данном давлении. в) Рассчитывают отношение коэффициентов теплоотдачи при кипении и вынужденном движении αкип /αw: если αкип /αw˃2, то α=αкип если αкип /αw˂0,5, то α=αw если 0,5 ˂αкип /αw ˂2, то α=αwεкип где 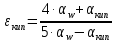 - поправочный коэффициент на теплоотдачу при кипении. - поправочный коэффициент на теплоотдачу при кипении.Если теплоносителем является излучающий газ, то в этом случае теплообмен между газом и стенкой происходит путем конвективного и лучистого теплообмена. Тогда коэффициент теплоотдачи находят по формуле 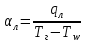 где qл – плотность теплового потока, переданного излучением, Вт/м2; Тг – температура газа, 0С. Плотность лучистого теплового потока находят поформуле Нуссельта: 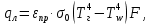 где 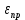 – приведенная степень черноты; – приведенная степень черноты; 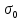 = 5,67-108 Вт/(м2·К4) – постоянная Стефана–Больцмана; Tг и Tw – температуры газа и стенки, К. = 5,67-108 Вт/(м2·К4) – постоянная Стефана–Больцмана; Tг и Tw – температуры газа и стенки, К.Приведенную степень черноты рассчитывают по формуле 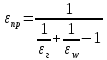 где 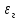 и и 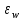 – степень черноты газа и поверхности соответственно. – степень черноты газа и поверхности соответственно.Степень черноты газа зависит от его состава, температуры и объема, который занимает газ. Для продуктов сгорания энергетических топливстепень черноты газа рассчитывают по формуле: 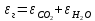 где 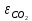 – степень черноты углекислого газа; * – степень черноты углекислого газа; *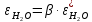 – степень черноты водяного пара; – степень черноты водяного пара; 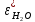 – условная степеньчерноты водяного пара; – условная степеньчерноты водяного пара; 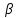 – поправочный коэффициент, учитывающий особенности излучения водяного пара. – поправочный коэффициент, учитывающий особенности излучения водяного пара.Степени черноты перечисленных газов определяют по номограммам, представленным на рис. 13–14 [1] на которых графически изображена зависимость 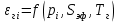 где рi – парциальное давление i – го газа, кПа; Тг – температура газа, ºC (K); Sэф – эффективная длина пути луча, м. Для газового объема произвольной формы эффективную длину пути луча рассчитывают по формуле 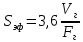 где Vг – объем, занимаемый газом, м3; Fг – площадь оболочки, в которую заключен газ, м2. Поправочный коэффициент 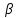 находят по номограммена рис. 15 [1] в виде находят по номограммена рис. 15 [1] в виде 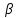 = =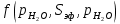 . .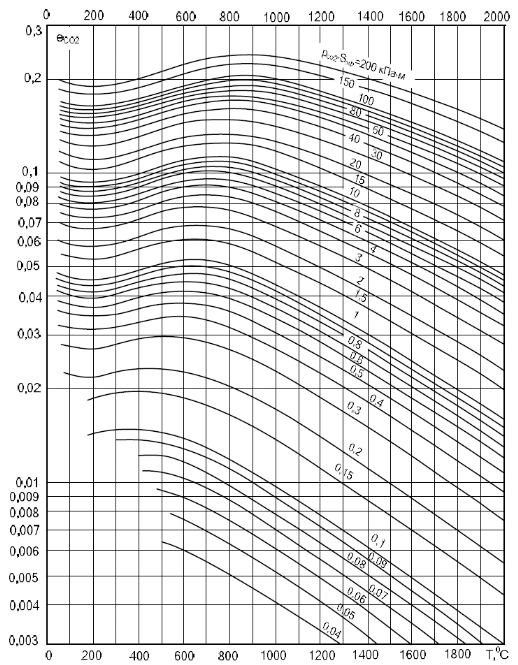 Рис. 13. Степень черноты двуокиси углерода 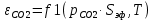 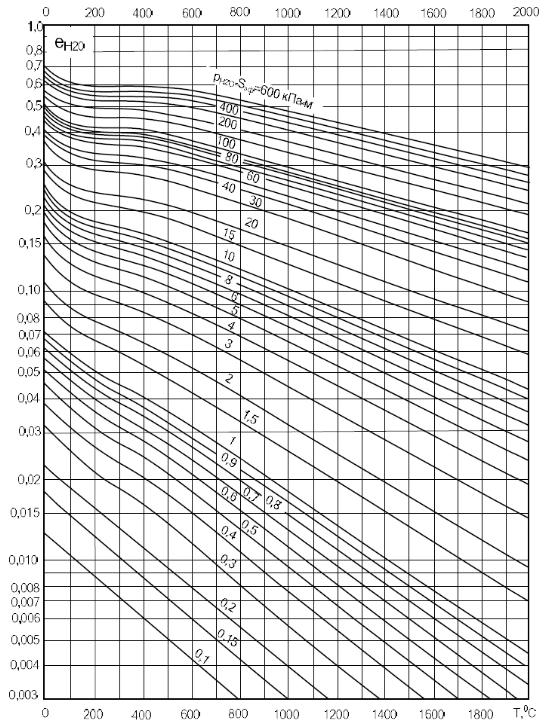 Рис. 14. Степень черноты водяного пара εН2О=f2(pН2O·Sэф, T) 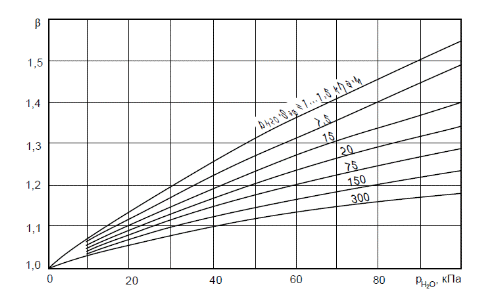 Рис. 15. Поправочный коэффициент β на парциальное давление для водяного пара Поверхность теплопередачи Величина поверхности теплообмена F, м2, определяется из основного уравнения теплопередачи 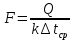 где Q–тепловая нагрузка аппарата (определяется из теплового баланса); k– коэффициент теплопередачи; Δtср– средний температурный напор. Поповерхноститеплообменаподбираютсятеплообменныйаппаратипатрубки. Конструктивные размеры аппаратаСодержание конструктивного расчета зависит от особенностей выбранной конструкции аппарата, т. е. от выбора поверхности теплообмена: трубчатая, пластинчатая, спиральная и т. д. Площадь поперечного сечения канала рассчитывают по формулам : — круглая одиночная труба с внутренним диаметром dвн 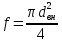 — n круглых труб с внутренним диаметром dвн 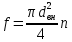 — кольцевой канал теплообменника типа «труба в трубе» 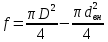 где D – внутренний диаметр наружной трубы, м; dнар – наружный диаметр внутренней трубы, м; При движении теплоносителя в каналах сложной формы в качестве определяющего размера принимают эквивалентный диаметр который равен: -для щелевого канала пластинчатого теплообменника 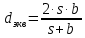 где b – ширина пластины, м; s – расстояние между пластинами, м; 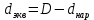 - для кольцевого канала теплообменника типа «труба в трубе» - для кольцевого канала теплообменника типа «труба в трубе»где D – внутренний диаметр наружной трубы, м; dнар – наружный диаметр внутренней трубы, м; - для внешнего канала прохода теплоносителя в межтрубном пространстве кожухотрубного теплообменника с числом трубок n 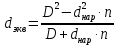 где D – внутренний диаметр кожуха, м; dнар – наружный диаметр внутренних трубок, м. При движении теплоносителя в изогнутых трубах (коленах, змеевиках) происходит его дополнительная турбулизация и, как следствие, увеличение коэффициента теплоотдачи. Для расчета теплоотдачи в изогнутых трубах необходимо число Нуссельта умножить на поправочный коэффициент: 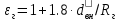 где Rг – радиус гиба (изгиба), м. Для кожухотрубчатых аппаратов, имеющих наибольшее распространение в промышленности, технологических процессах, по поверхности теплообмена Fопределяются количество труб, их размещение в трубной решетке, диаметр корпуса аппарата, число ходов в трубном и межтрубном пространстве и размеры входных и выходных патрубков. Количество труб 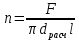 где dрасч – расчетный диаметр трубы; при α1> α2 dpacч=dн, при α1= α2 dpacч= 0,5 (dн + dв), при α 1< α2dpacч=dв; l – длина трубы (выбирается по ГОСТ 53677 -2009). Трубы в трубных решетках размещаются по вершинам равносторонних треугольников или по сторонам правильных шестиугольников, что одно и то же (ромбическое размещение), и по концентрическим окружностям. Ромбическое размещение при большом количестве трубок дает меньшие размеры трубной решетки. Количество труб в трубных решетках рассчитывается по уравнениям n 3a(a 1) 1; b 2a 1, где n – общее количество труб; а – количество труб на стороне наибольшего шестиугольника; b – количество труб на диагонали наибольшего шестиугольника. Шаг труб S(расстояние между осями соседних труб) обычно выбирают равным 1,3…l,5dн, но не меньше dн + 6 мм. Общее количество труб должно быть таким, чтобы а и bбыли целыми числами. Внутренний диаметр корпуса аппарата рассчитывают по уравнениям для одноходовых аппаратов 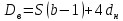 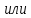 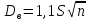 для многоходовых 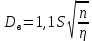 где S – шаг труб; n – число труб; η – коэффициент заполнения трубной решетки, η = 0,6…0,8. Расчетное значение диаметра корпуса округляется до ближайшего размера диаметра [7]. Расстояние между трубными решетками (активная длина трубок) определяется по формуле 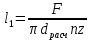 где 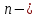 число трубок в одном ходу; z число трубок в одном ходу; z 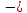 число ходов. число ходов.Длина трубок не должна превышать 6 м. В многоходовых аппаратах рекомендуется выбирать четное число ходов. Если при выборе многоходового теплообменника длина труб получается выше допустимой, необходимо изменить или диаметр, или скорость движения теплоносителя, или обе эти величины. Полная высота кожухотрубчатого теплообменника складывается из активной длины труб и высоты коллекторов 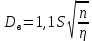 где S – шаг труб; п – число труб; η – коэффициент заполнения трубной решетки, η = 0,6…0,8. Расчетное значение диаметра корпуса округляется до ближайшего размера диаметра [7]. Расстояние между трубными решетками (активная длина трубок) определяется по формуле 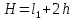 где h — высота коллектора, которую выбирают из конструктивных соображений равной 200…400 мм. Для спирального теплообменника исходными данными для конструктивного расчета являются поверхность теплообмена F, ширина канала b, толщина листов σ и высота спиралей h. Шаг спирали S = b + δ, где b = 6…15 мм; σ = 2…8 мм. Каждый полувиток спирали строится по радиусам r1 и r2, которые для первых витков равны 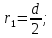 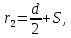 где d — диаметр первого витка внутренней спирали (выбирается исходя из конструктивных соображений). Центры, из которых производят построение спиралей, отстоят друг от друга на величину шага витка S. Длина спирали при числе витков n равна 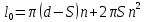 Число витков спирали 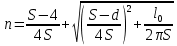 Наружный диаметр спирального теплообменника D = d + 2nS + δ. Высота спиралей h принимается равной 375…750 мм по [8]. Определение диаметров патрубков Диаметры патрубков, м, для входа и выхода теплоносителей определяют по формуле 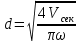 где Vсек — секундный расход жидкости, пара или газа, м3/с; ω — скорость жидкости, пара или газа, м/с. |
