Главная страница
Навигация по странице:

  • Найти

  • Ответ

  • Найти: : Решение

  • Дано

  • Найти: . Решение

    		•

    Контрольная работа по теоретической механике. Контрольная по т.м.. Решение Из уравнения 3 определяем


    Скачать 0.51 Mb.
    НазваниеРешение Из уравнения 3 определяем
    АнкорКонтрольная работа по теоретической механике
    Дата09.11.2020
    Размер0.51 Mb.
    Формат файлаdoc
    Имя файлаКонтрольная по т.м..doc
    ТипРешение
    #148973

    Контрольная работа по теоретической механике.

    Вариант №18.
    Задача С1: Жесткая рама расположена в вертикальной плоскости, закреплена в точке А шарнирно, а в точке В прикреплена опорой на катках. В точке С к раме привязан трос, перекинутый через блок и несущий на конце груз весом . На раму действует пара сил с моментом и две силы в точках H и D соответственно. Определить реакции связей.
    Дано: ; ; ; ; .


    Найти: .

    Решение:
    1. ;

    2. ;

    3. ;

    Из уравнения 3 определяем :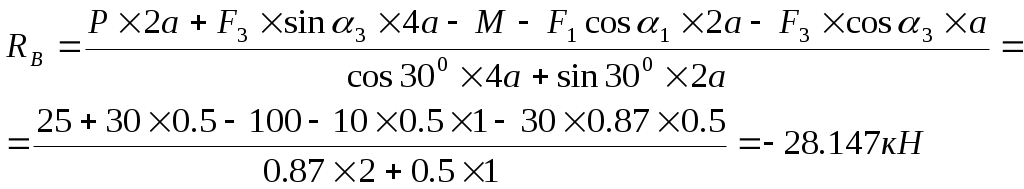


    Из уравнения 2 определяем :

    Из уравнения 1 определяем :

    Проверка:



    Ответ: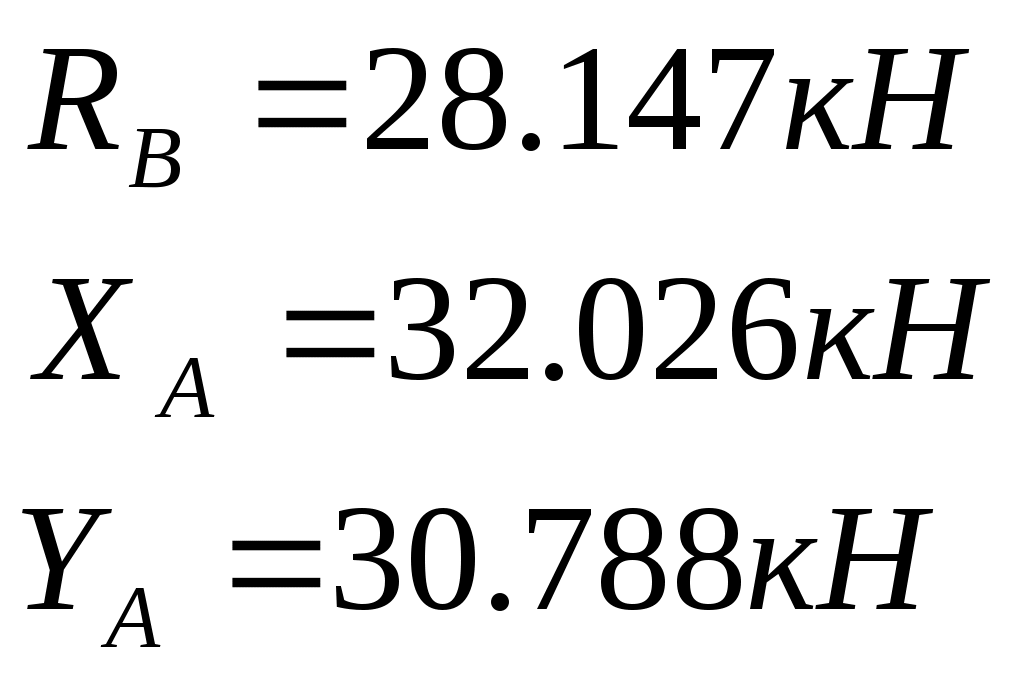

    Задача С4: Две однородные прямоугольные плиты жестко соединены под прямым углом и закреплены в точке А сферическим шарниром, в точке В цилиндрическим шарниром, и невесомым стержнем l.

    Размеры плит указаны на рисунке; Вес большей плиты , меньшей . Каждая из плит расположена параллельно одной из координатных плоскостей.

    На плиты действует пара сил и две силы.

    Определить реакции связей.
    Дано:


    Найти: :
    Решение:

    1. ;

    2. ,

    3.

    4.

    5.

    6.

    Из уравнения 6 определяем:

    Из уравнения 2 определяем:

    Из уравнения5 определяем:

    Из уравнения 4 определяем:

    Из уравнения 1 определяем:

    Из уравнения 3 определяем:

    Для проверки возьмем ось , прохо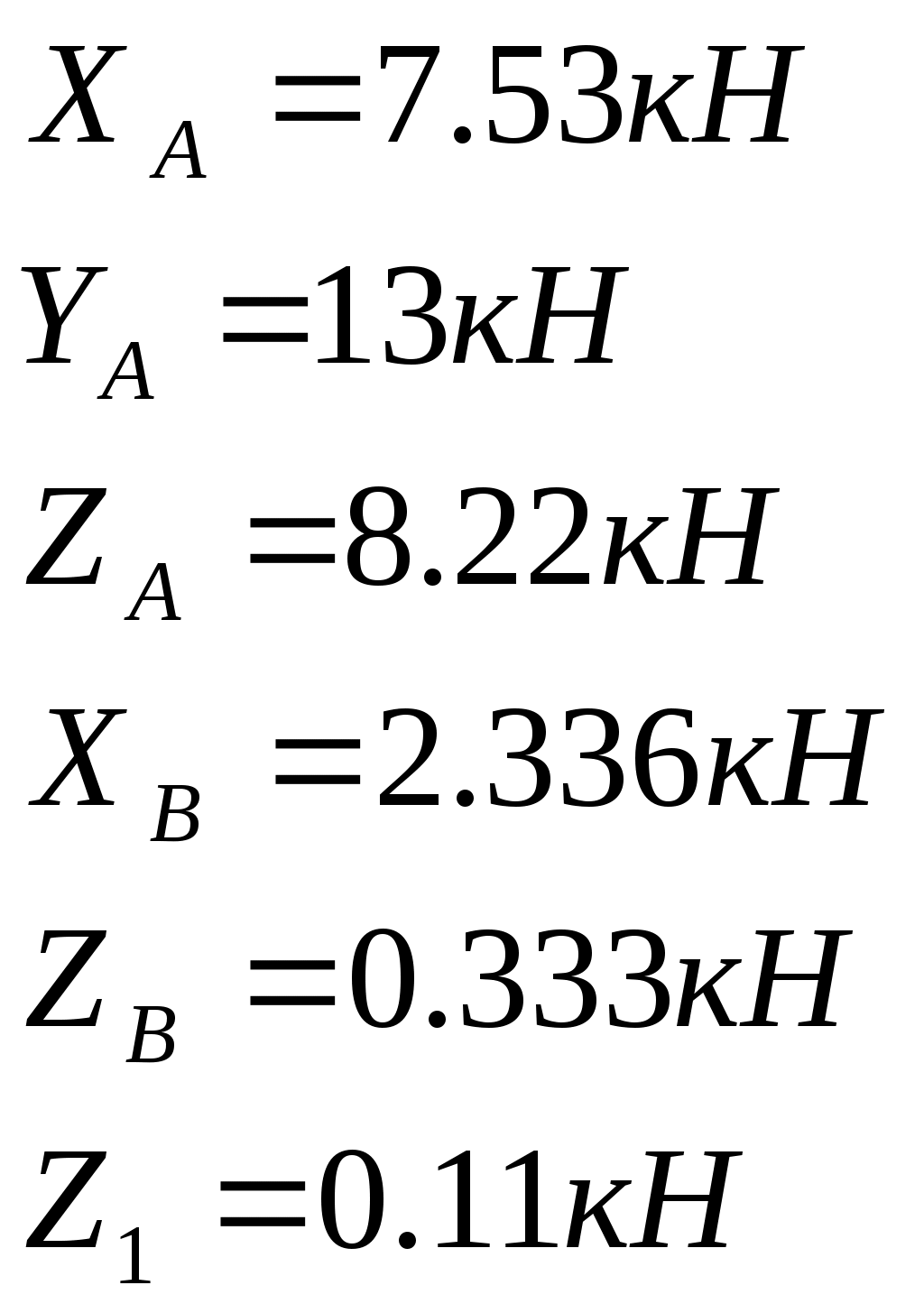дящую через центр тяжести плиты 2:




    Ответ:

    Задача К1:

    а. Точка В движется в плоскости xy по законам, заданным в таблице. Найти уравнение траектории точки для момента времени . Определить ее скорость и нормальное и касательные ускорения.

    б. Точка движется по дуге радиуса R=2м, по закону, заданному в таблице. Определить скорость и ускорение точки для момента времени . Показать на рисунке векторы скорости и ускорения точки.
    Дано:

    Найти:
    а. Определим уравнение движения точки: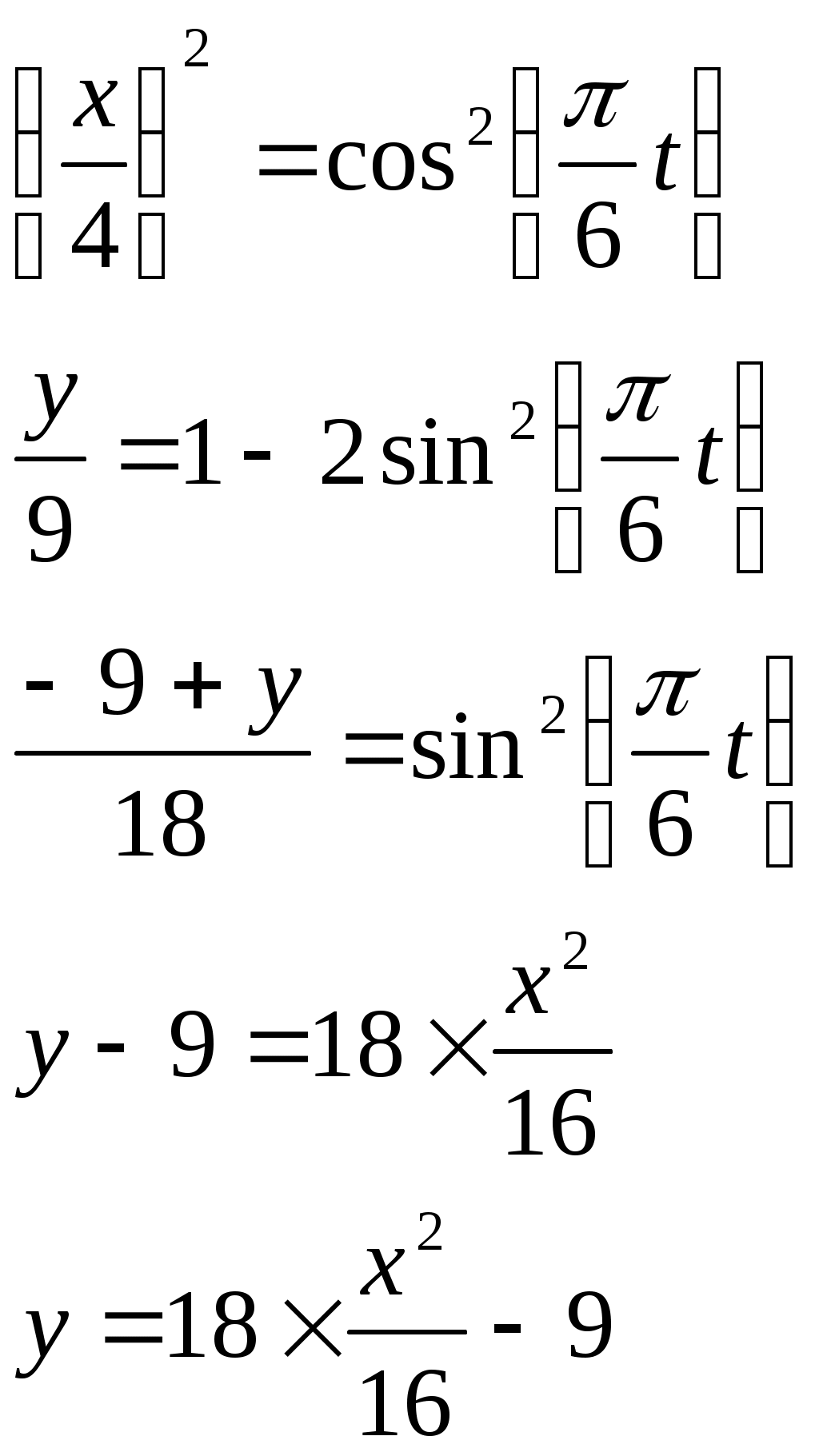


    График движения точки: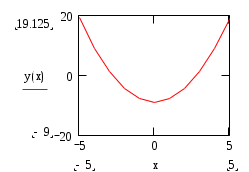


    Определим скорость движения точки: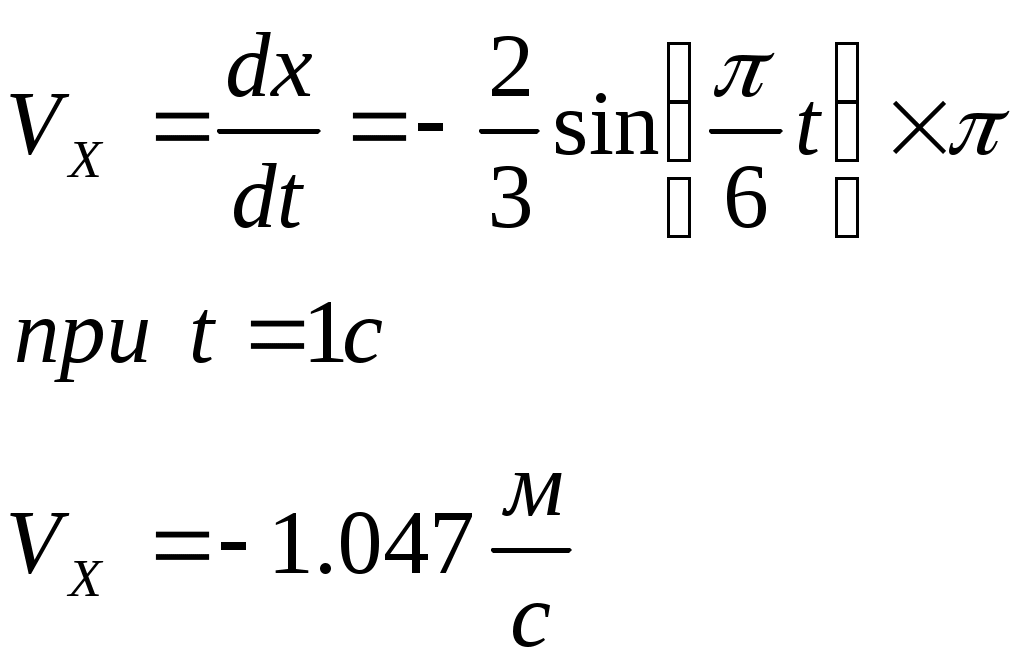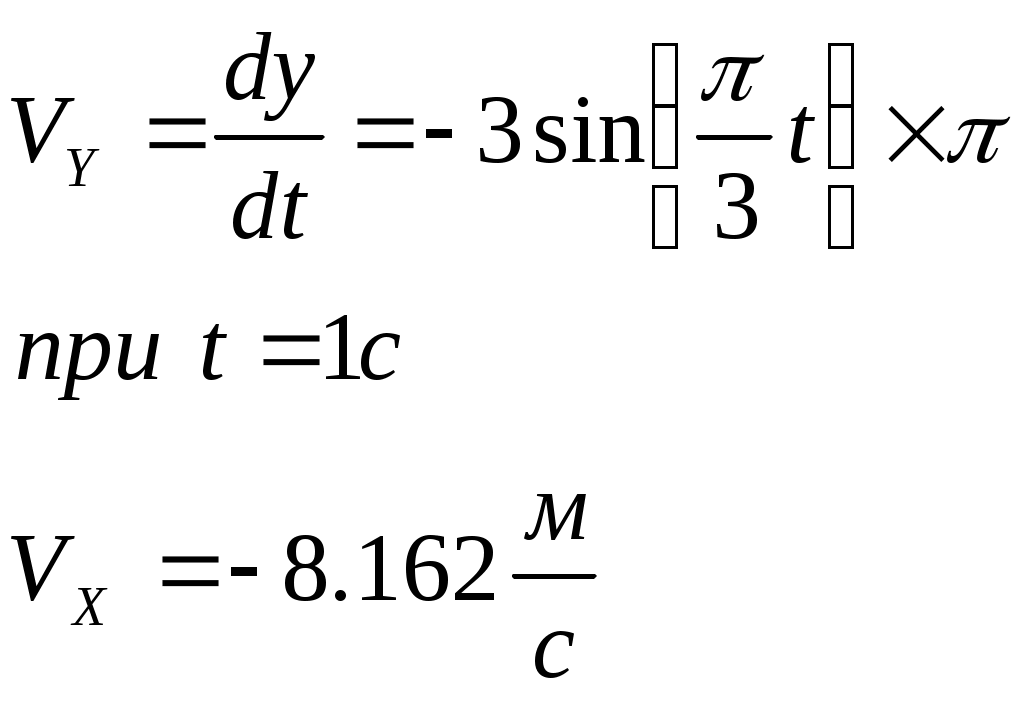



    Определим ускорение точки: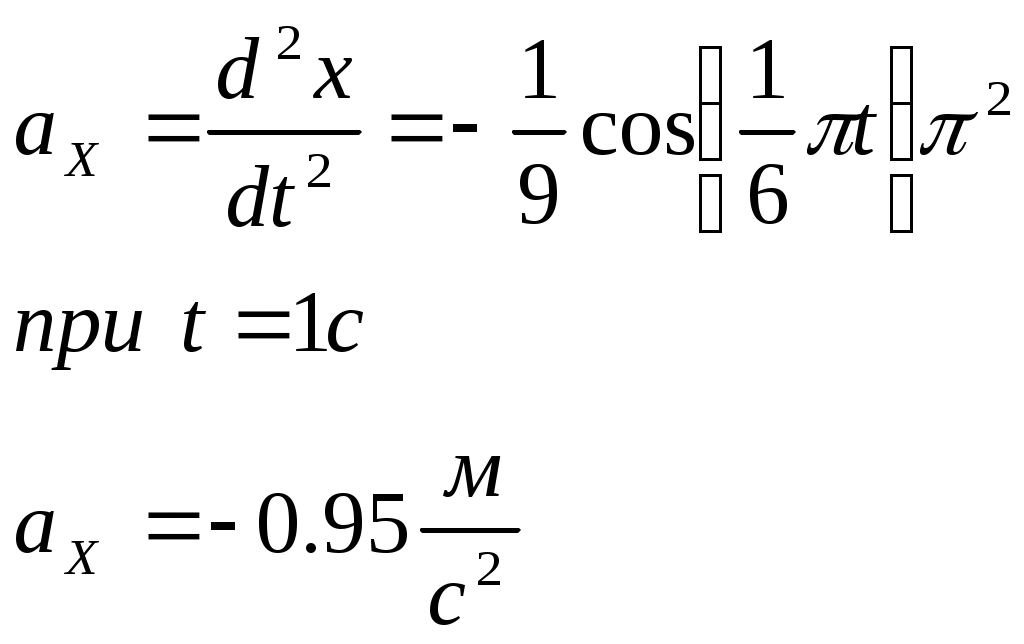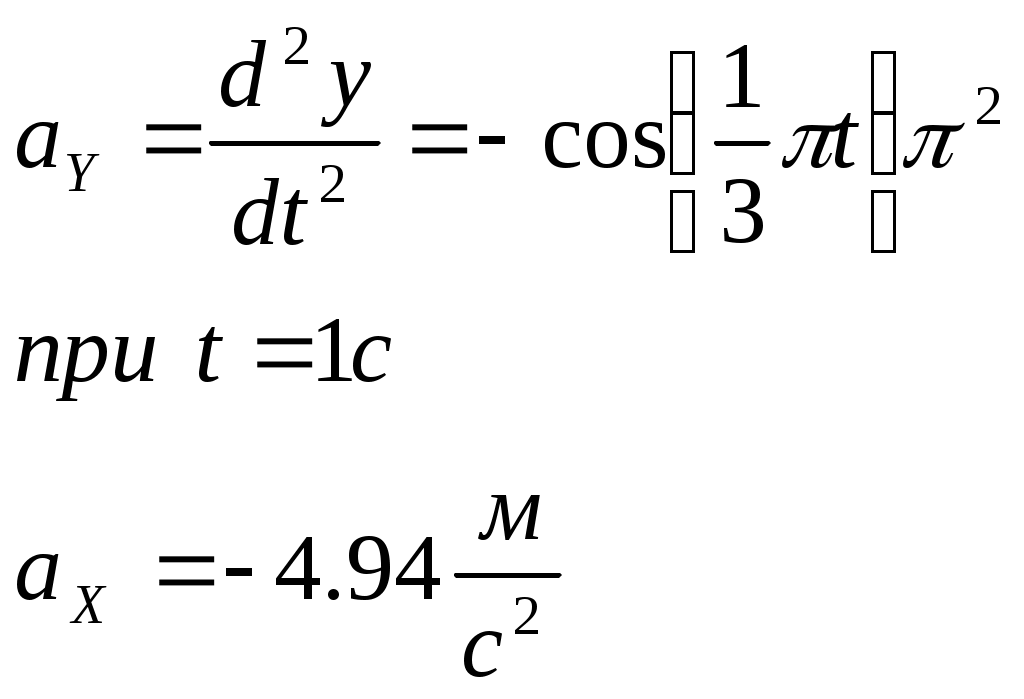



    Определим нормальное и касательное ускорения точек и радиус кривизны траектории движения: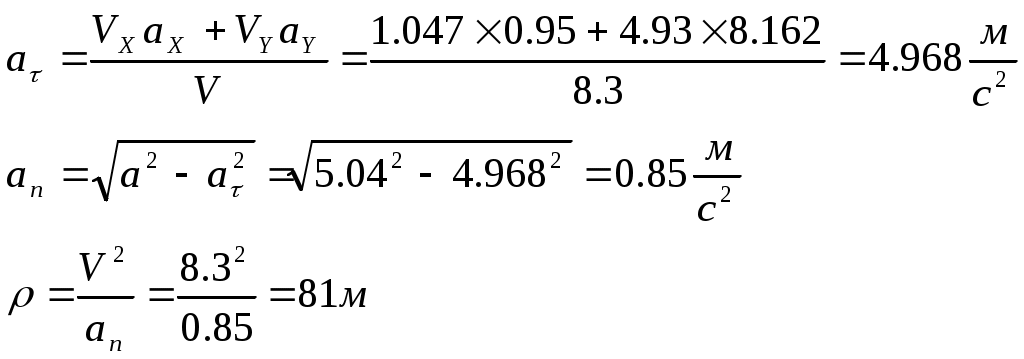

    б. Определяем скорость точки: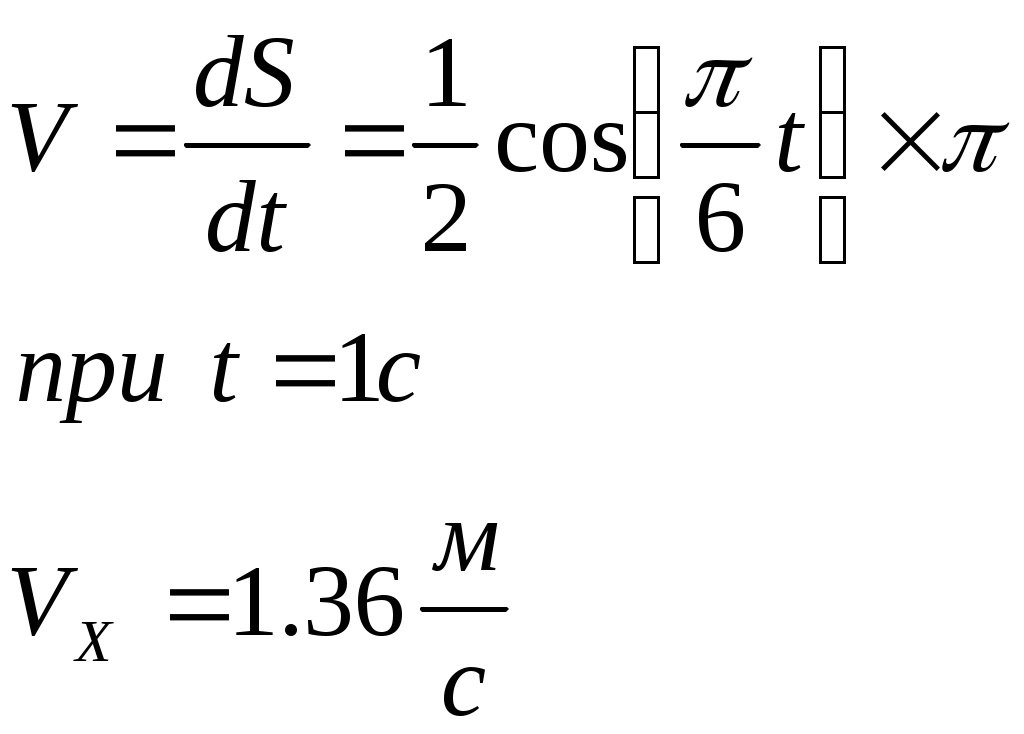

    Определяем ускорение точки: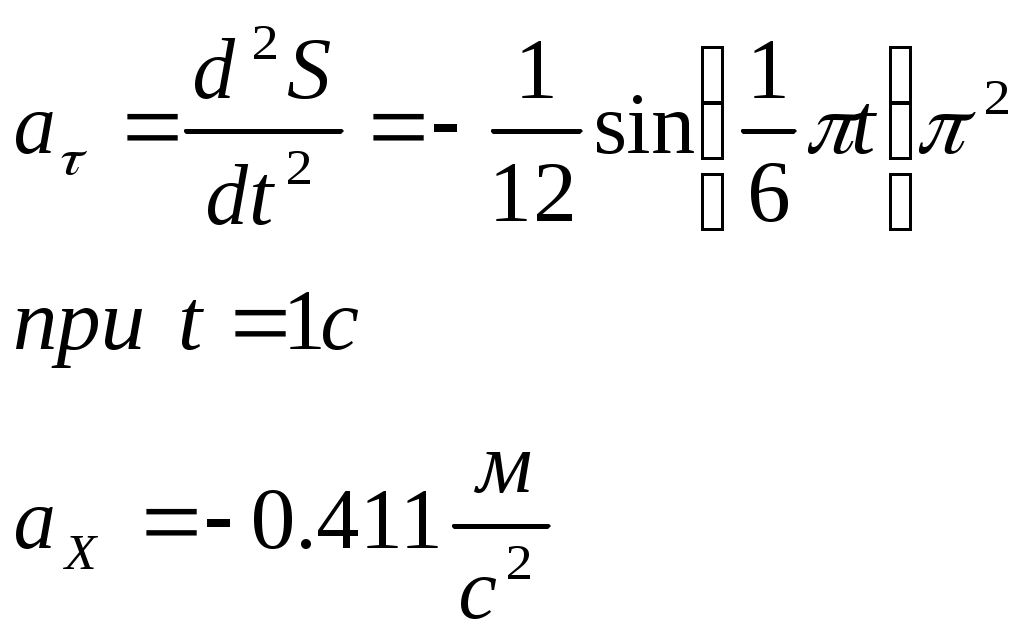





    Ответ: а.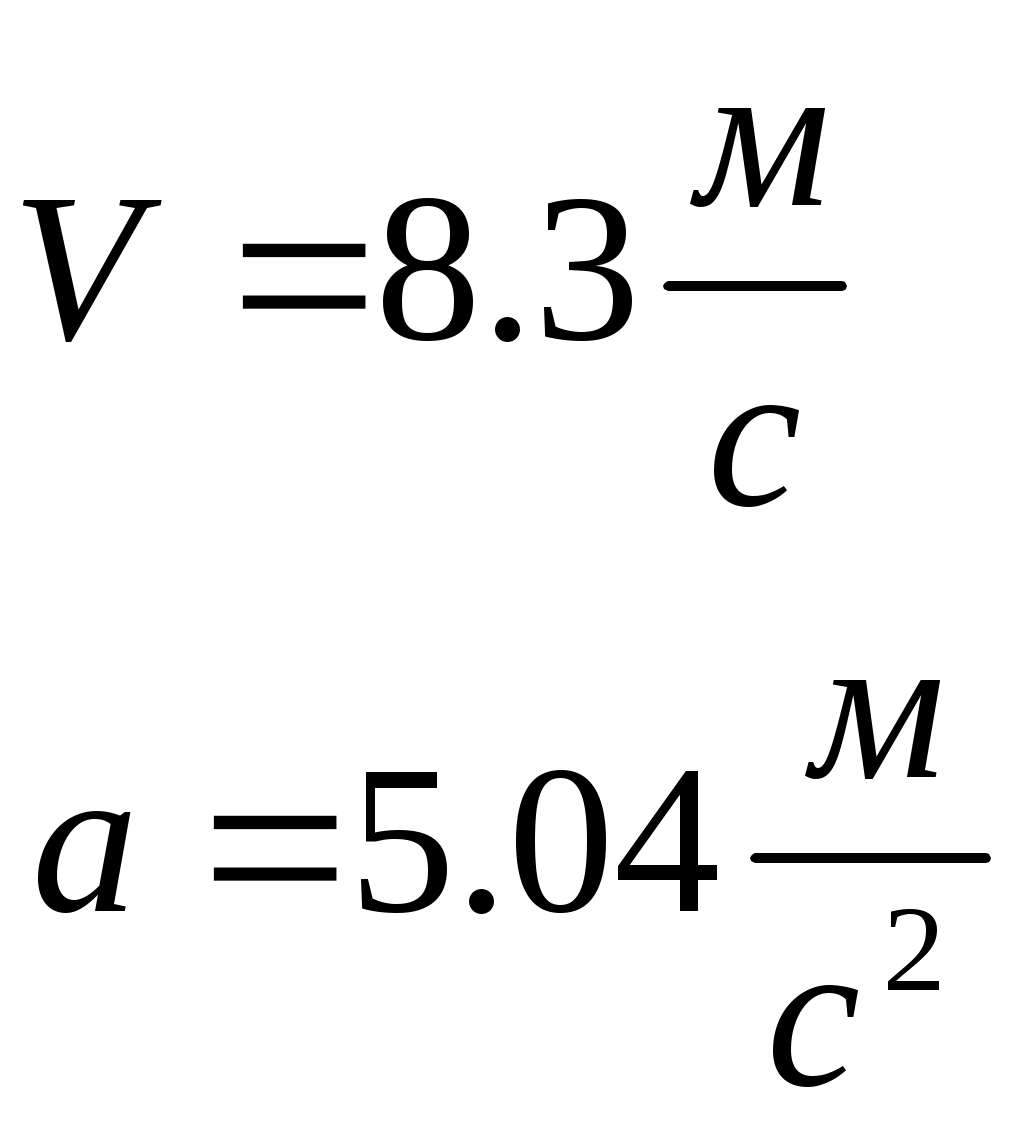

    б.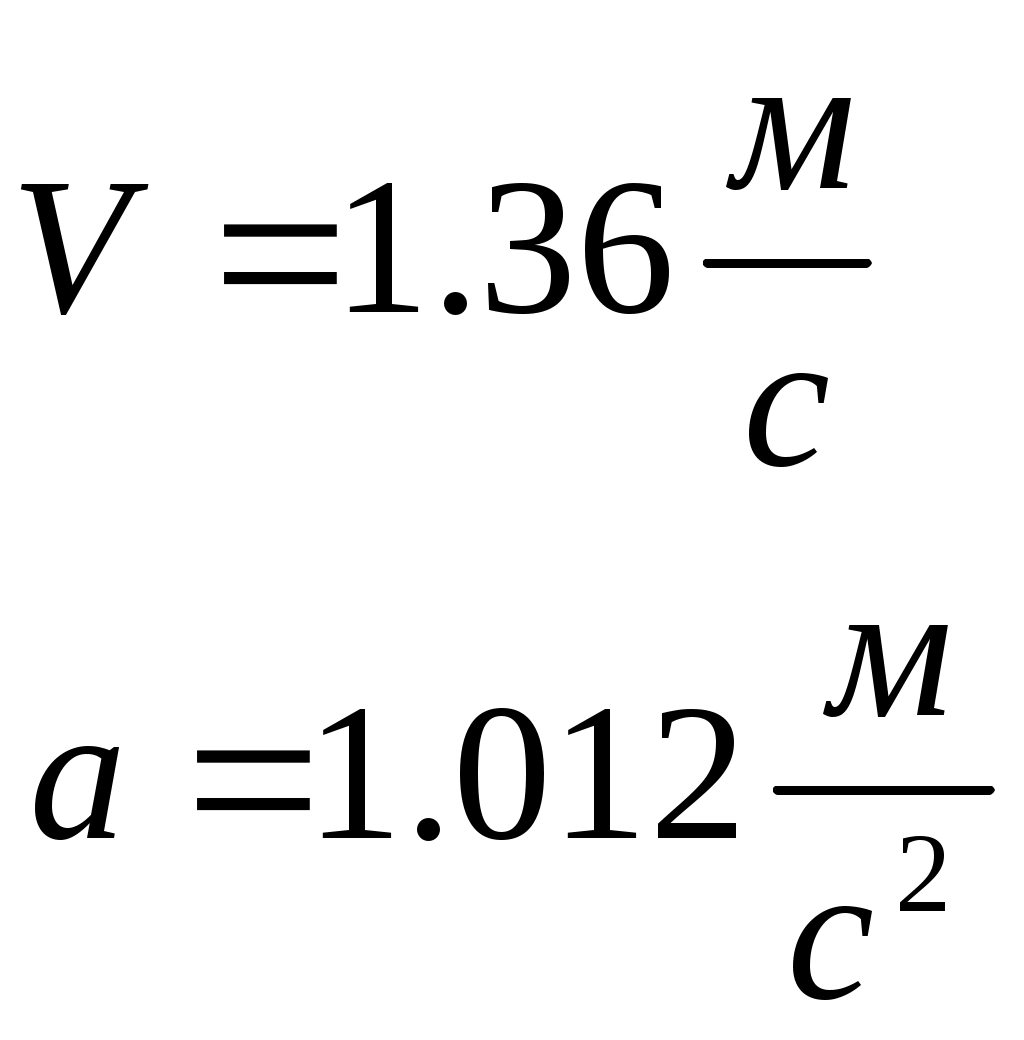

    Задача К3:

    Плоский механизм состоит из стержней 1, 2, 3, 4 и ползуна Е, соединенных друг с другом и неподвижными осями О1 и О2 шарнирами; точка D находится в середине стержня AB. Длины стержней . Положение механизма задано углами .

    Определить величины, указанные в таблицах в столбце «Найти».

    Заданную угловую скорость угловое ускорение считать направленными по часовой стрелке.
    Дано:


    Найти: .
    Решение:
    Строим положение механизма. Определяем скорости соответствующих точек с помощью мгновенного центра скоростей:

    Определяем скорости точек D и B: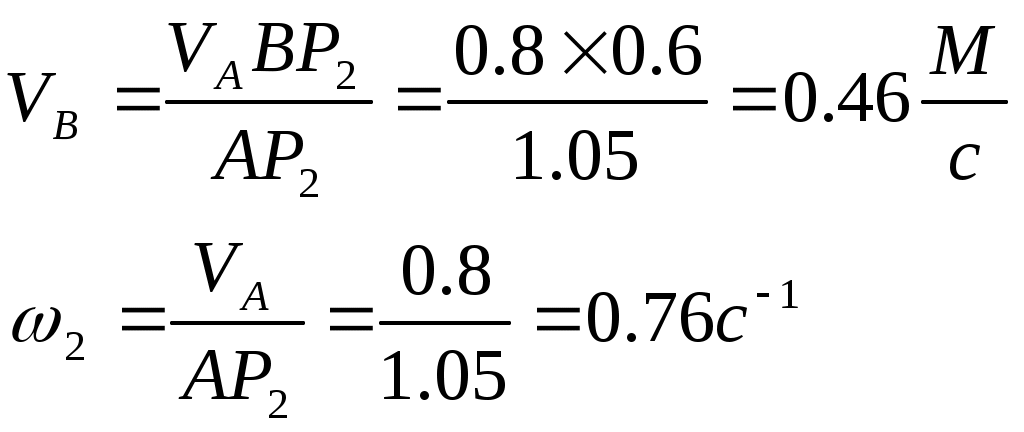








    Определим скорость точки Е: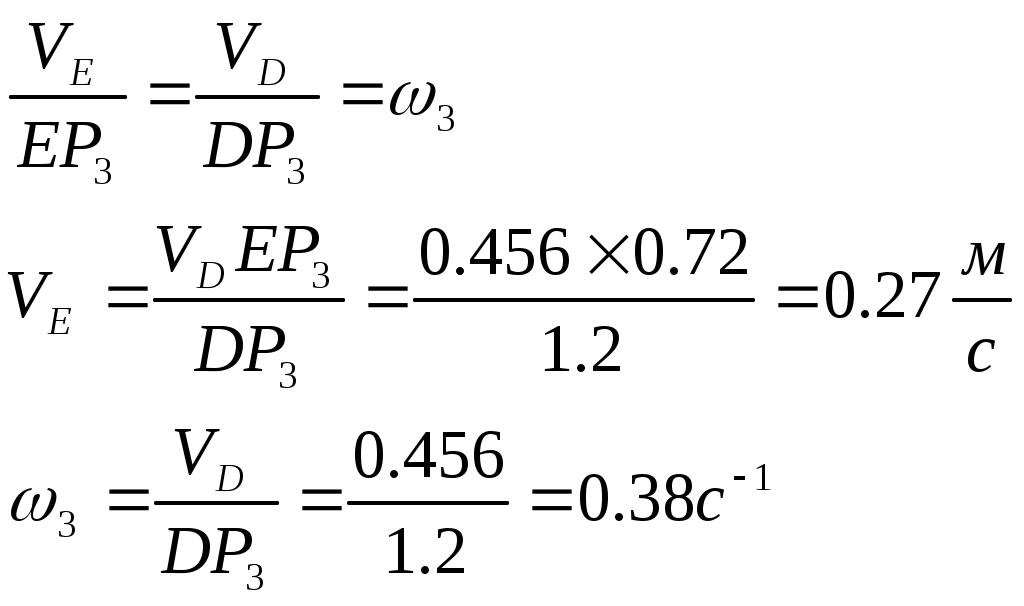

    Определим ускорение точки В: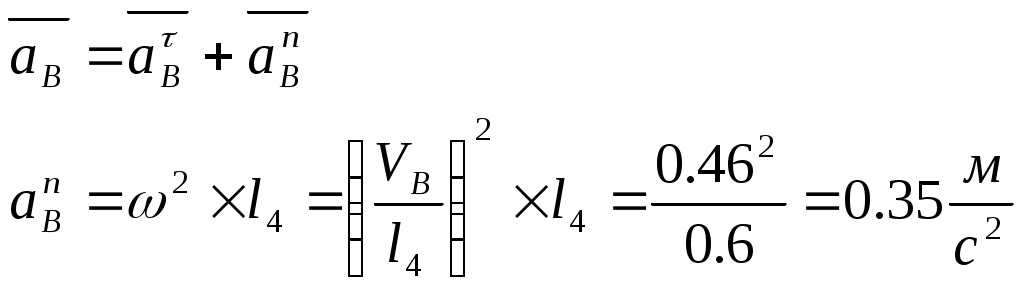










    Спроектируем векторы ускорений на направление ВА:
    1. - Паралле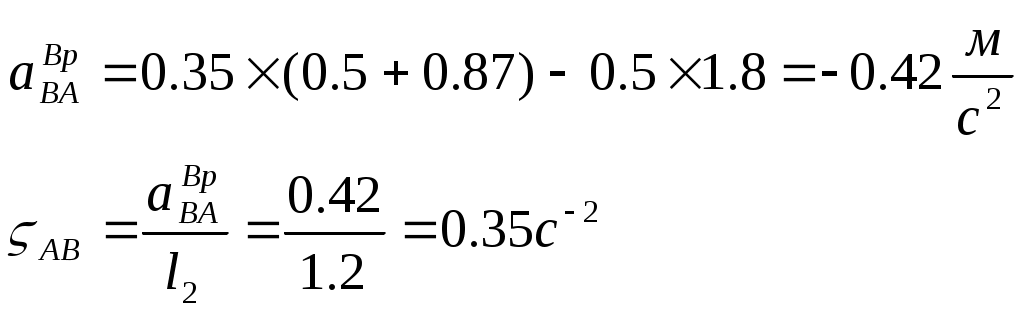льно ВА
    2. - Перпендикулярно ВА
    Из 1:
    Из 2:
    Ответ:

    Параметр
    VD, м/с
    VЕ, м/с
    ωAB, c-1
    aB, м/с2
    εAB, c-2

    Значение
    0.456
    0.27
    0.76
    1.83
    0.35


    Задача К4: Прямоугольная пластина вращается вокруг неподвижной оси по закону: . По пластине вдоль прямой BD движется точка М, закон ее относительного движения которой .

    Найти абсолютную скорость и абсолютное ускорение точки М в момент времени t=1c.
    Дано:

    Найти:
    Решение:



    1. Относительное движение:
    Установим, где будет находиться точка М в момент времени t=1c:

    Знак минус говорит о том, что точка находится ниже точки А.
    Определим значения скорости и ускорения в относительном движении: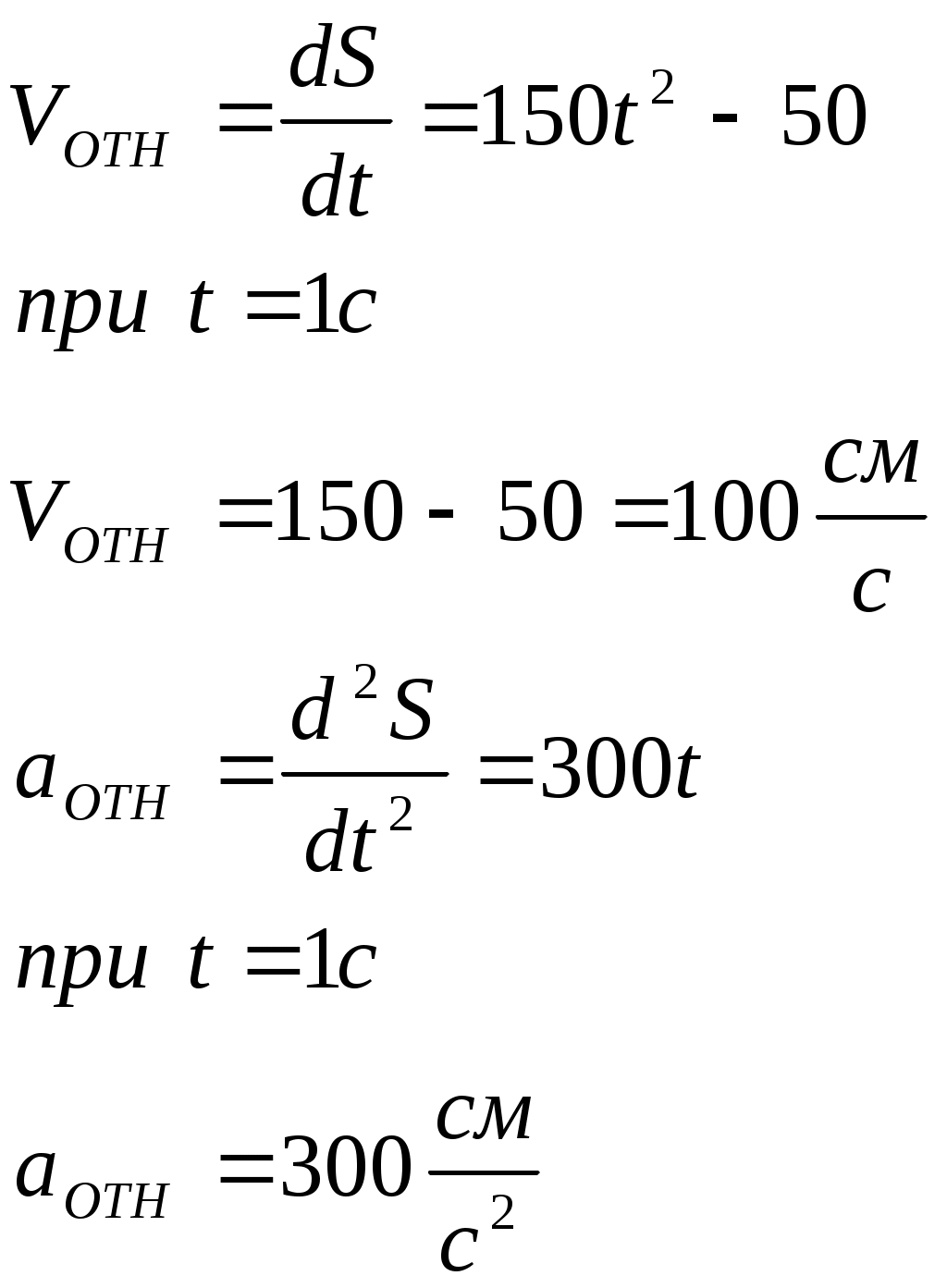

    2. Переносное движение: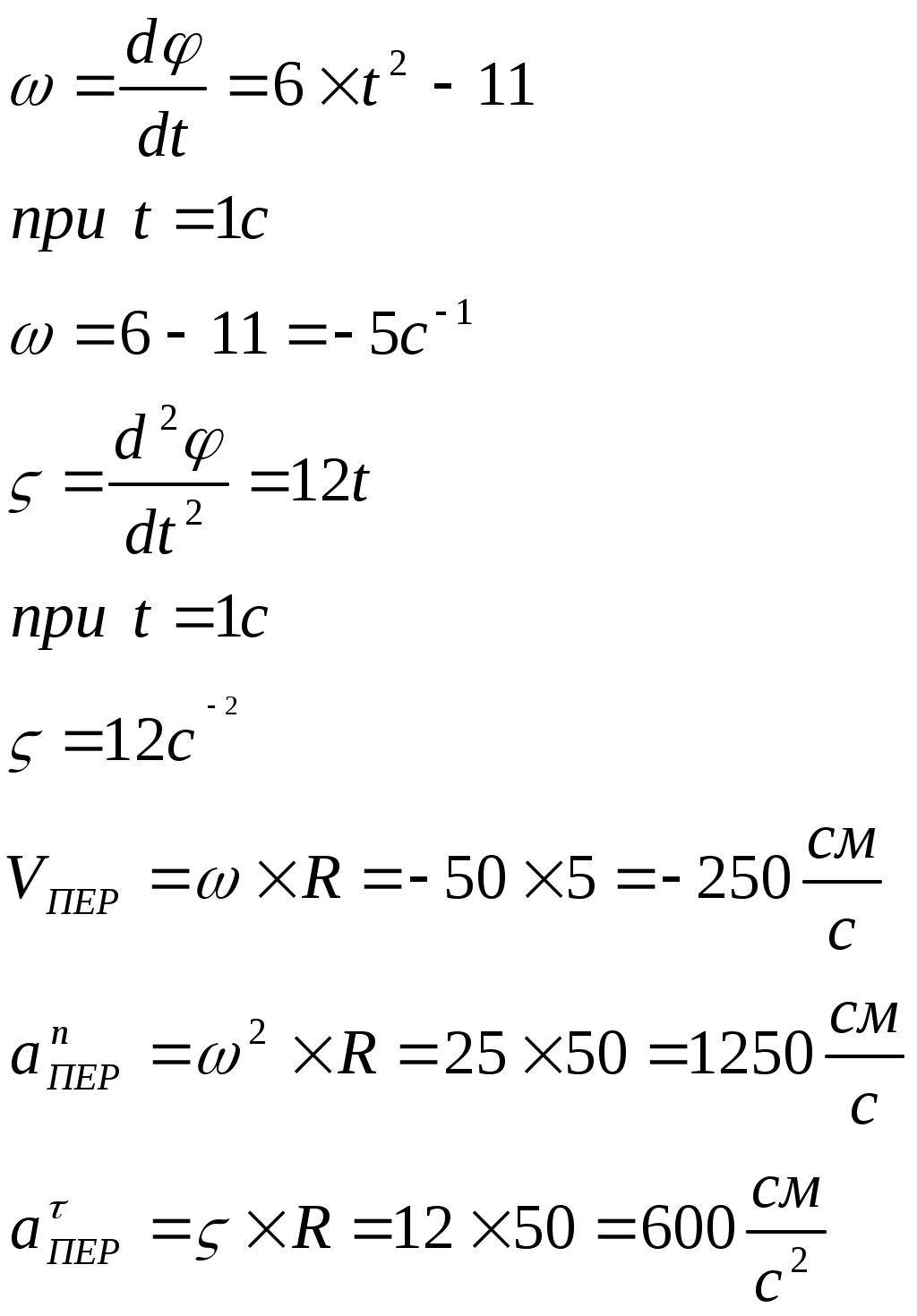

    3. Ускорение Кориолиса:

    4. Определяем абсолютную скорость точки М:
    Разложим векторы скоростей на две оси и определим соответственно две составляющих абсолютной скорости: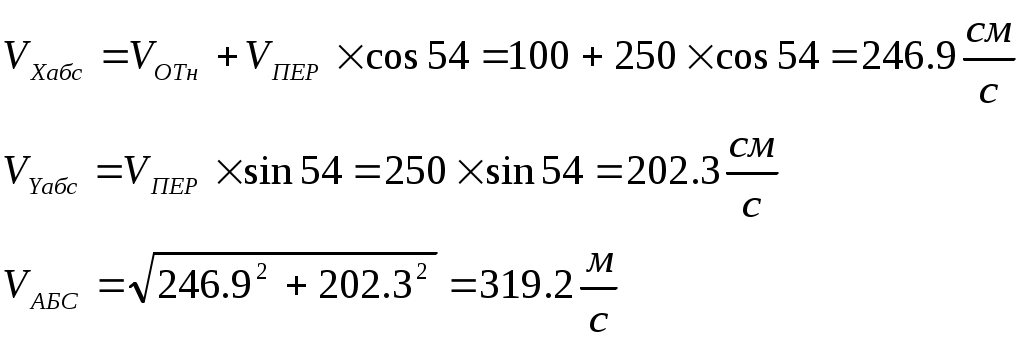

    5. Определим абсолютное ускорение точки М:
    Разложим векторы ускорений на две оси и определим соответственно две составляющих абсолютного ускорения: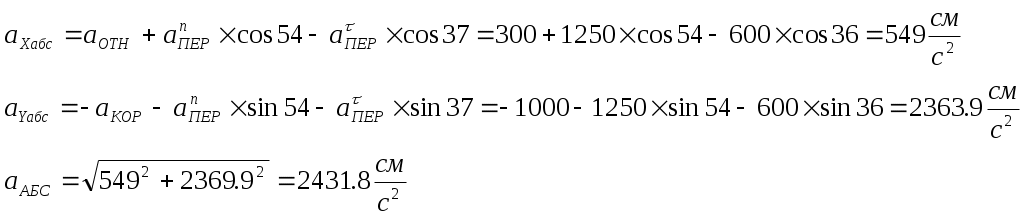

    Ответ:


    Министерство образования и науки Российской Федерации.
    Курганский государственный университет.
    Кафедра теоретической механики и сопротивления материалов.


    Контрольная работа по теоретической механике.
    Выполнил студент группы _______ /__________________/

    Вариант №18


    Проверил преподаватель /__________________/

    Курган 2005 г.

    написать администратору сайта