Экономический анализ. МОР 23.12.2016 Вариант 6. Решение 1 Составить экономикоматематическую модель задачи

• Название: Решение 1 Составить экономикоматематическую модель задачи
• Анкор: Экономический анализ
• Дата: 01.06.2021
• Размер: 158 Kb.
• Имя файла: МОР 23.12.2016 Вариант 6.doc
• Тип: Решение; #212446

Вариант 6

1. Предприятие выпускает 2 вида продукции, используя 3 вида ресурсов. Принятые обозначения: А – матрица норм затрат сырья, В – запасы ресурсов, С – прибыль на единицу продукции:

А = 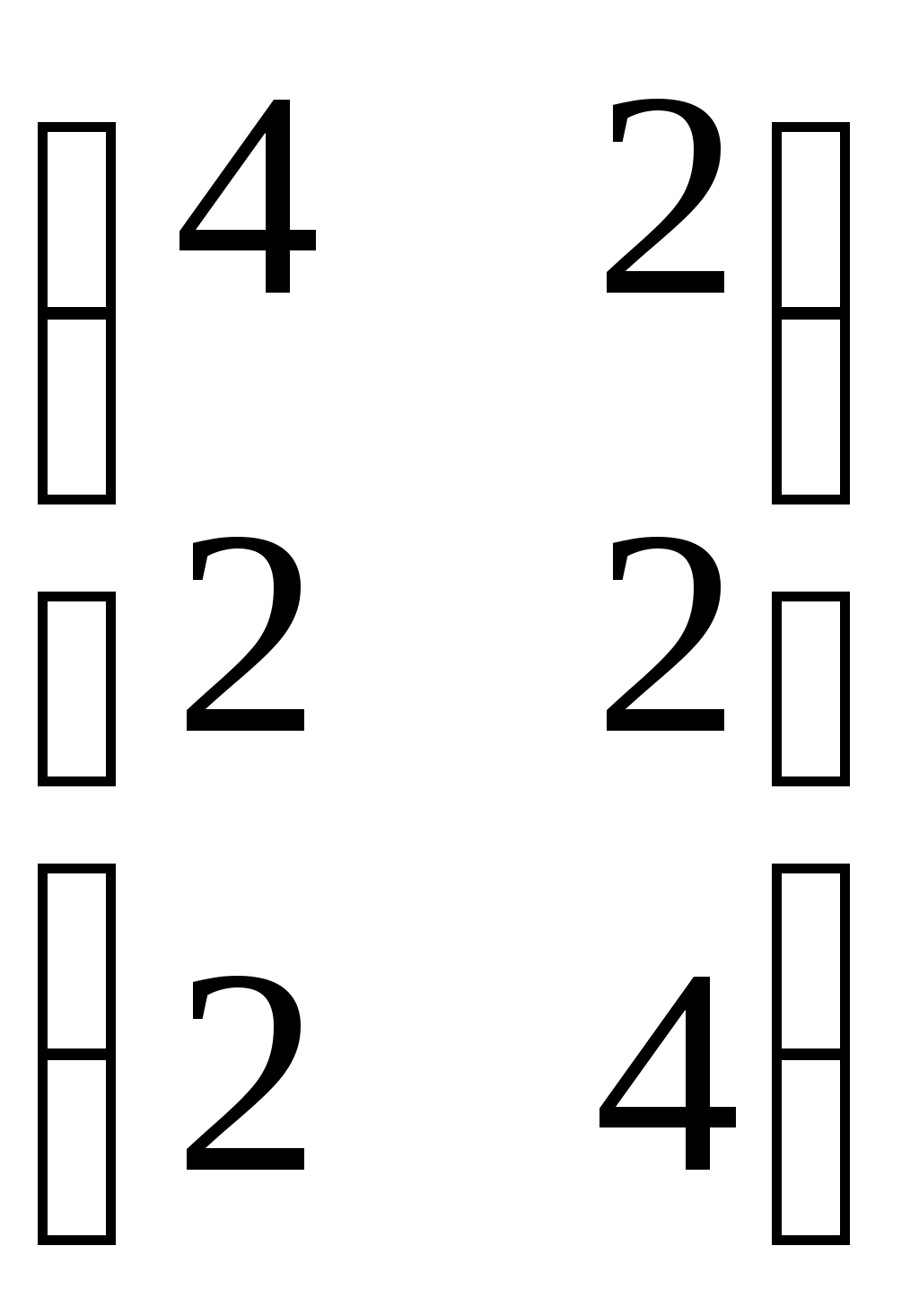, В = , С = .

Требуется:

1) Составить экономико-математическую модель задачи;

2) Определить план выпуска изделий (геометрическим способом и симплекс-методом), обеспечивающий получение максимальной прибыли;

3) Составить двойственную задачу, найти оптимальное решение и оптимум двойственной задачи с помощью теорем двойственности; указать дефицитные для предприятия ресурсы;

4) Определить интервалы устойчивости двойственных оценок ресурсов;

5) Проанализировать, как изменится максимальная прибыль предприятия в результате изменение запаса 1-го ресурса на 5 единиц.

Решение:

1) Составить экономико-математическую модель задачи;

Обозначим х1 – количество продукции 1 вида, х2 – кол-во продукции 2 вида.

Целевая функция – суммарная прибыль:

F=2x₁+4x₂ → max

О граничения по ресурсам:

4x₁+2x₂≤80, (1)

2x₁+2x₂≤60, (2)

2x₁+4x₂≤100, (3)

x₁ ≥ 0, x₂ ≥ 0.
2) Определить план выпуска изделий (геометрическим способом и симплекс-методом), обеспечивающий получение максимальной прибыли;

Графический метод:

Строим область допустимых решений, удовлетворяющих ограничениям:

4x₁+2x₂≤80, (1)

x1	0	20
x2	40	0

2x₁+2x₂≤60, (2)

x1	0	30
x2	30	0

2x₁+4x₂≤100, (3)

x1	0	50
x2	25	0

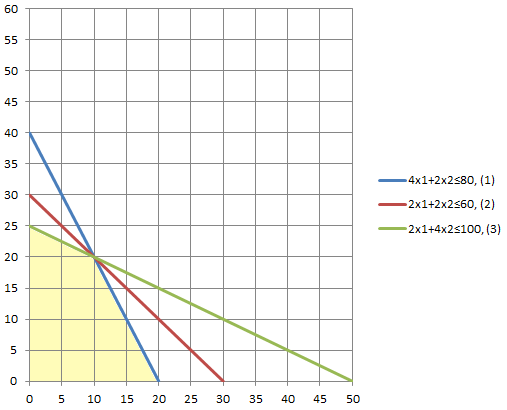А

В

Из рисунка видно, что точка максимума это любая точка из отрезка АВ.

П римем, что оптимум достигается в точке А:

2x₁+4x₂=100

x₁=0

Откуда:

x₁ = 0, x₂ = 25

F(X) = 2*0 + 4*25 = 100
Симплекс-метод:

К анонический вид ограничений:

4x₁ + 2x₂ + 1x₃ + 0x₄ + 0x₅ = 80

2x₁ + 2x₂ + 0x₃ + 1x₄ + 0x₅ = 60

2x₁ + 4x₂ + 0x₃ + 0x₄ + 1x₅ = 100

Используем симплекс таблицу:

Базисные переменные	Свободные члены	x1	x2	x3	x4	x5	Отношение
x3	80	4	2	1	0	0	40
x4	60	2	2	0	1	0	30
x5	100	2	4	0	0	1	25
F=	0	-2	-4	0	0	0	0

Вместо переменной x₅ в план войдет переменная x₂.

Базисные переменные	Свободные члены	x1	x2	x3	x4	x5	Отношение
x3	30	3	0	1	0	-0.5
x4	10	1	0	0	1	-0.5
x2	25	0.5	1	0	0	0.25
F=	100	0	0	0	0	1

Оптимальный план:

x₁ = 0, x₂ = 25

F(X) = 2*0 + 4*25 = 100

Решения, полученные симплекс-методом и графическим методом, совпадают.

3) Составить двойственную задачу, найти оптимальное решение и оптимум двойственной задачи с помощью теорем двойственности; указать дефицитные для предприятия ресурсы.

Z=80y₁+60y₂+100y₃→ min

4 y₁+2y₂+2y₃≥2

2y₁+2y₂+4y₃≥4

y₁≥ 0, y₂≥ 0, y₃≥ 0

Найдем решение двойственной задачи, используя теоремы двойственности:

П одставим с систему ограничений прямой задачи оптимальное решение:

4*0+2*25=50<80

2*0+2*25=50<60

2*0+4*25=100

Следовательно, y1=0, y2=0,

Поскольку х2=25, а х1=0:

2*0+2*0+4y₃=4

Откуда

y₁ = 0, y₂ = 0, y₃ = 1

Z(Y*) = 80*0+60*0+100*1 = 100=F(X*)
4) Определить интервалы устойчивости двойственных оценок ресурсов;

Поэтому необходимо найти такие интервалы изменения каждого из свободных членов системы ограничений исходной ЗЛП, в которых оптимальный план двойственной задачи не менялся бы.

При этом условие устойчивости двойственных оценок задачи исходит из выражения

X¹=X⁰+ΔX=A^-1(B+ΔB)

в которой компоненты вектора X¹ должны быть неотрицательны, т.е. все x_j≥0. На этом основании для нашей задачи можно записать:

0 ,33 0 -0,17 -0,33 1 -0,33 -0,17 0 0,33

8 0+∆ b1 60+∆ b2 ≥0 100+∆ b3

О тсюда получаем условие устойчивости:

0.33Δb₁-0.17Δb₃+10≥0

-0.33Δb₁+Δb₂-0.33Δb₃+0≥0

-0.17Δb₁+0.33Δb₃+20≥0

Затем последовательно находим интервалы устойчивости:

Пусть Δb₂=Δb₃=0, Δb₁≠0. Получим:

Δ b₁≥-30,

Δb₁≥0,

Δb₁≥-120

Интервал изменения равен:

(b₁ - ∆b₁^-; ∞)=[80-30; +∞] = [50;+∞]
Пусть Δb₁=Δb₃=0, Δb₂≠0. Получим:

Δb₂≥0,

Интервал изменения равен:

(b₂ - ∆b₂^-; ∞)=[60-0; +∞] = [60;+∞]
Пусть Δb₁=Δb₂=0, Δb₃≠0

Δ b₃≤60,

Δb₃≤0,

Δb₃≥-60

Интервал изменения равен:

(b₃ - ∆b₃^-; b₃ + ∆b₃⁺)=[100-60; 100+0] = [40;100]
5) Проанализировать, как изменится максимальная прибыль предприятия в результате изменение запаса 1-го ресурса на 5 единиц.

Новый запас этого ресурса равен b1 + Δb1 = 80 + 5 = 85 и лежит в интервале устойчивости, поэтому его влияние на величину максимальной стоимости продукции можно определить с помощью теоремы об оценках.

∆Z₁ = y₁∆b₁ = 0 *5 = 0

Тогда целевая функция F(x) составит на величину:

F(x*) = F(x) + y1 Δb1 = 100 + 0 * 5 = 100.

Данное мероприятие является неэффективным.


2. Биржевой маклер хочет вложить в акции некоторую сумму денег с тем, чтобы к концу года иметь 10 тыс. долл. Существует два типа акций, в которые стоит делать вложения: акции надежных компаний с минимальным риском («голубые фишки»), приносящие в среднем 10% годовых, и акции компаний, занимающихся высокими технологиями. Последние акции имеют более высокую доходность – в среднем 25% годовых, однако они значительно более рисковые. Поэтому маклер решил вкладывать в них не более 60% средств. На какую сумму и каких акций надо приобрести маклеру, чтобы достичь желаемой цели?

Решение:

Пусть х1 – сумма, вкладываемая в акции надежных компаний, х2 – сумма, вкладываемая в акции компаний, занимающихся высокими технологиями.

Целевая функция – годовой доход от вложения:

F=0.1x₁+0.25x₂ → max

Ограничения:

1. 
   Биржевой маклер хочет к концу года иметь 10 тыс. долл. Сумма в конце года складывается из инвестиций плюс годовой доход:
   

1.1x₁+1.25x₂ =10

2. Маклер решил вкладывать в рискованные компании не более 60% средств

x₂ ≤ 0,6(x₁+x₂)

откуда:

-0,6 x₁+0,4x₂ ≤ 0
Математическая модель:

F =0.1x₁+0.25x₂ → max

1.1x₁+1.25x₂ =10

-0,6 x₁+0,4x₂ ≤ 0

x₁, x₂ ≥0

Решим задачу графическим методом:

Строим область допустимых решений, удовлетворяющих ограничениям:

1.1x₁+1.25x₂ =10

x1	0	9,09
x2	8	0

-0,6 x₁+0,4x₂ ≤ 0

x1	1	0,67
x2	1,5	1

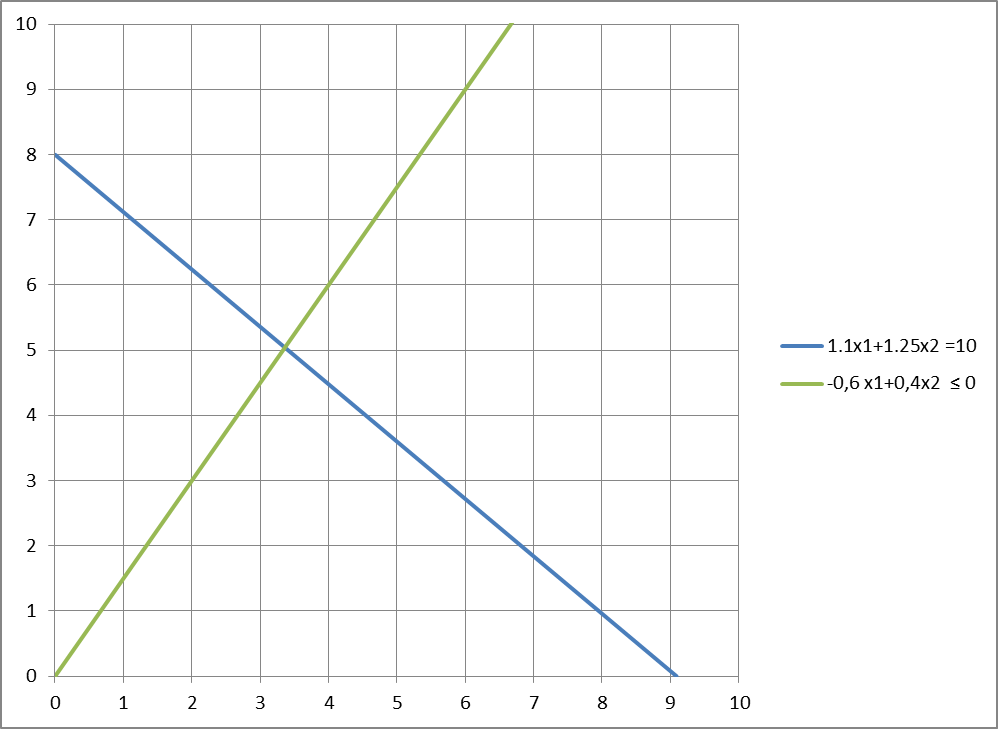А

Из рисунка видно, что точка максимума – точка А:

1 ,1x₁+1,25x₂=10

-0.6x₁+0.4x₂=0

Откуда:

x₁ = 3,36, x₂ = 5,04

F(X) = 0,1*3,36+0,25*5,04 = 1,6

Ответ: следует вложить в акции надежных компаний 3,36 тыс. долл., а в акции компаний, занимающихся высокими технологиями, 5,04 тыс. долл. Тогда к концу года будет сумма 10 тыс. долл. за счет годового дохода в 1,6 тыс. долл.