ФКП и операционное исчисление. Матем_решение. Решение Поле является потенциальным, если ротор этого поля равен нулю
 Скачать 79.53 Kb. Скачать 79.53 Kb.
|
|
Контрольная 5 4.2 Доказать потенциальность заданного векторного поля и найти его потенциал, используя криволинейный интеграл. 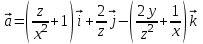 Решение: Поле является потенциальным, если ротор этого поля равен нулю. 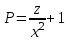 ; ; 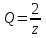 ; ; 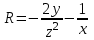 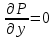 ; ; 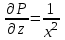 ; ;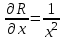 ; ; 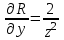 ; ;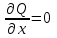 ; ; 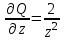 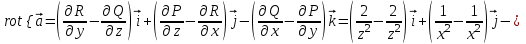 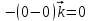 Значит, данное векторное поле потенциально. Потенциал 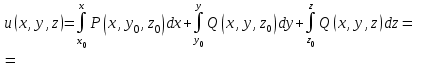 . . В качестве начальной точки возьмем точку М01;1;1. Тогда 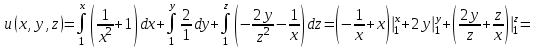 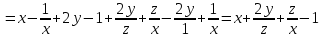 Ответ: 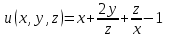 Контрольная 7 2.2 Пользуясь условиями Коши Римана, установить дифференцируемость функции f(z) и найти f'(z0). 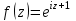 , z0 = 0 , z0 = 0Решение: Поскольку z = x + yi, то: 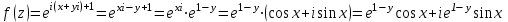 Действительная часть функции f(z): 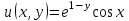 Мнимая часть функции f(z): 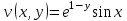 Проверим выполнение условий Коши-Римана: Найдем 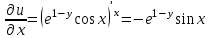 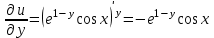 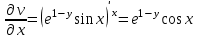 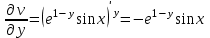 Условия Коши-Римана: 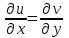 , , 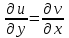 . . Очевидно, что эти условия выполняются. Тогда можно найти производную: 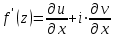 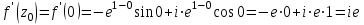 Ответ: 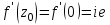 3.2 Вычислить интеграл от функции комплексного переменного по данной кривой. 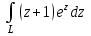 , L: {|z|=1, Re z0} , L: {|z|=1, Re z0}Решение: Под интегралом аналитические функции, значит, интеграл по кривой не зависит от кривой, а только от концов кривой и можно применить интегрирование по частям.  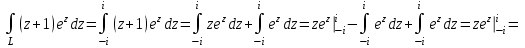 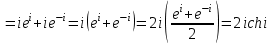 Ответ: 2ichi 6.2 Найти решение задачи Коши, используя метод операционного исчисления x'' − 4x = t2 + 6t – 2, x(0) = 0, x'(0) = 0; Решение: Перейдем от оригиналов к изображениям: L[x(p)] = X(p); L[x'(p)] = pX(p) – x(0) = pX(p) – 1; L[x''(p)] = p2X(p) – px(0) – x'(0) = p2X(p) – 0 – 0 = p2X(p); L[t2] = 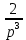 ; L[6t] = ; L[6t] = 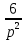 ; L[2] = ; L[2] = 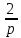 ; ;Запишем уравнение для изображений: p2X(p) – 4X(p) = 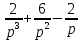 X(p)(p2 – 4) = 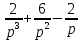 X(p)(p2 – 4) = 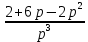 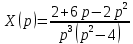 Решим уравнение для изображений. Разложим дробь на простейшие дроби: 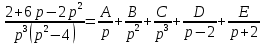 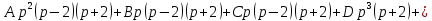 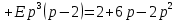 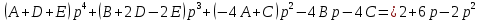 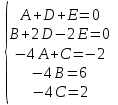 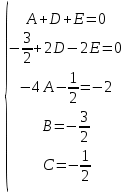 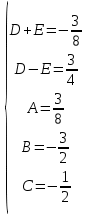 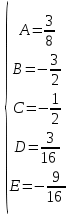 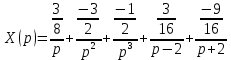 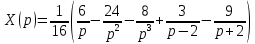 Найдем оригинал для функции. 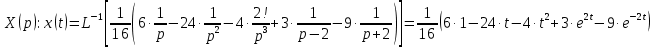 = =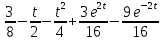 Ответ: 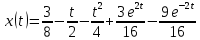 7.2 Методом операционного исчисления найти частное решение заданной системы дифференциальных уравнений 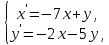 x(0)=1, y(0)=0 x(0)=1, y(0)=0Решение: Перейдем от оригиналов к изображениям: L[x(p)] = X(p); L[x'(p)] = pX(p) – x(0) = pX(p) – 1; L[y(p)] = Y(p); L[y'(p)] = pY(p) – y(0) = pY(p). Запишем систему для изображений: 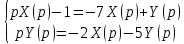 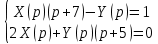 Найдем решение системы по формулам Крамера. 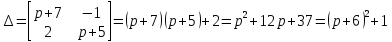 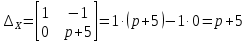 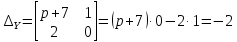 Получаем: 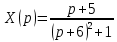 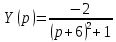 Возвращаемся к оригиналам: 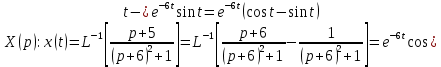 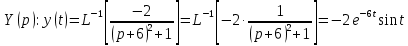 Получили решение: 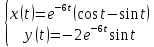 Ответ: 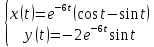 |
