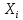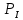математика пз 2. Решение Возможными значениями для X. Являются 0,1,2 Вычислим по формуле Бернулли вероятность каждого из значений случайной величины. Имеем p (x0) (0) 512
 Скачать 18.2 Kb. Скачать 18.2 Kb.
|
|
Задание для индивидуального решения в Excel Вероятность выиграть по лотерейному билету p=0,2. Куплено 3 билета. Случайная величина X – выигрыш по k билетам из купленных. Составить закон распределения вероятностей случайной величины, записать функцию распределения и построить ее график. Найти математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины X. Решение : Возможными значениями для X. Являются 0,1,2,3 . Вычислим по формуле Бернулли вероятность каждого из значений случайной величины. Имеем : P (x=0)= 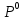 = = 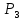 (0)= (0)=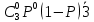 = =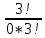 = =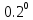 * *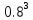 = =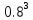 =0.512 =0.512P(X=1)= 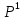 = =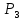 (1)= (1)=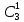 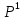 (1-P)2= (1-P)2=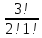 = =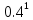 * *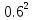 =0.384 =0.384P (x=2)= 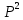 = =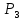 (2) (2)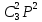 (1-P)= (1-P)=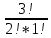 = =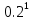 * *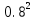 =0.096 =0.096P (X=3)= 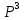 = =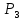 (3) (3)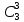 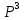 (1-P)0= (1-P)0=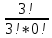 = =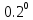 * *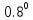 =0.008 =0.008Таким образом получили распределение :
Математическое ожидание равно M[X] = x1p1 + x2p2 + x3p3 + x4p4 = 0·0.512 + 1·0.384 + 2·0.096 + 3·0.008 = 0 + 0.384 + 0.192 + 0.024 = 0.6 дисперсия случайной величины равна разности математического ожидания квадрата случайной величины и квадрата её M[X] = x1p1 + x2p2 + x3p3 + x4p4 = 0·0.512 + 1·0.384 + 2·0.096 + 3·0.008 = 0 + 0.384 + 0.192 + 0.024 = 0.6 M[X2] = x12p1 + x22p2 + x32p3 + x42p4 = 02·0.512 + 12·0.384 + 22·0.096 + 32·0.008 = 0 + 0.384 + 0.384 + + 0.072 = 0.84 D[X] = M[X2] - (M[X])2 = 0.84 - (0.6)2 = 0.84 - 0.36 = 0.48 Поскольку дисперсия всегда неотрицательна, существует квадратный корень из дисперсии, который называется среднеквадратическим отклонением случайной величины X: Q=1.118 Функция распределения F(X)= 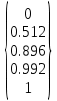 X≤0 0 1 2 X>3 |