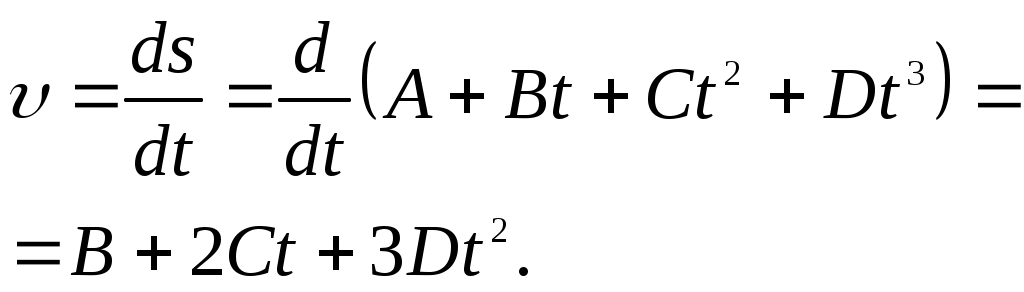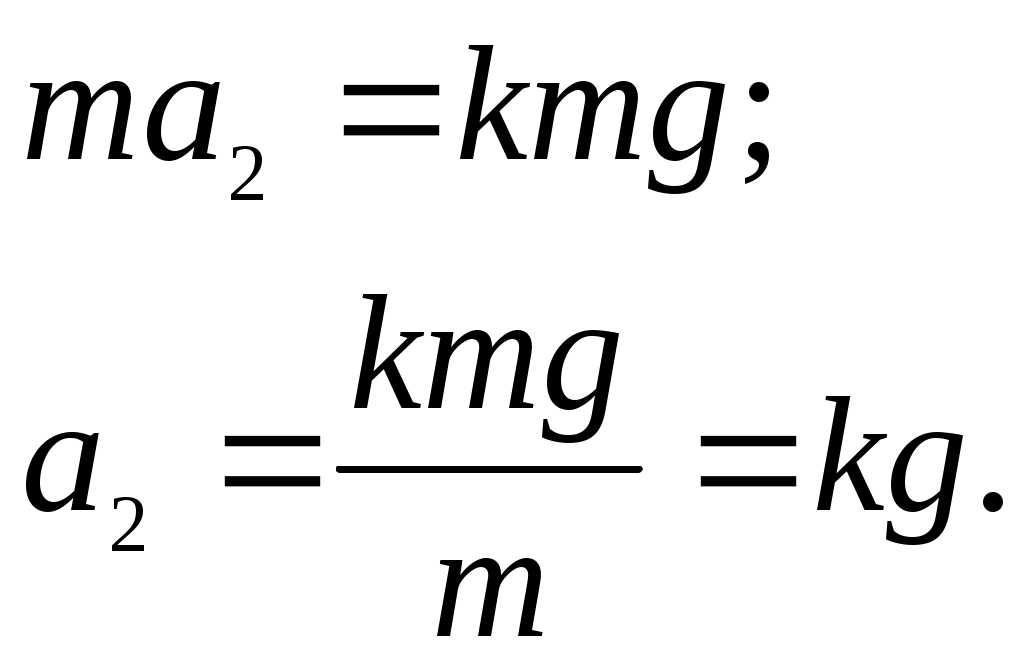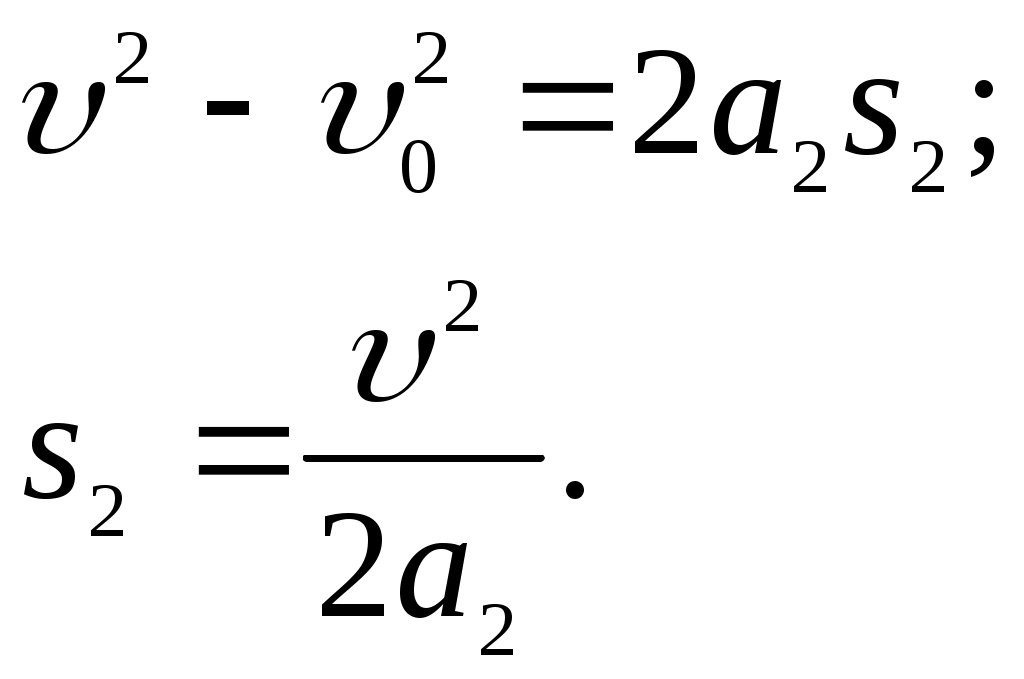Контрольная по ТОЭ. Решение_3713367. Решение 1) Мгновенная скорость есть первая производная пути по времени 1)

• Название: Решение 1) Мгновенная скорость есть первая производная пути по времени 1)
• Анкор: Контрольная по ТОЭ
• Дата: 05.03.2022
• Размер: 0.75 Mb.
• Имя файла: Решение_3713367.doc
• Тип: Решение; #384115
• страница: 1 из 2

Задача 1 (№ 4)

Зависимость пройденного телом пути от времени задается уравнением . Определите:

1) через сколько времени после начала движения ускорение тела будет равно ; 2) среднее ускорение тела за этот промежуток времени.

Дано: ; ; ; .	Решение 1) Мгновенная скорость есть первая производная пути по времени : (1.1)

Мгновенное ускорение – это первая производная от скорости по времени.

(1.2)

По условию, ускорение будет равно . Приравняв выражение (1.2) числу , получаем уравнение, из которого найдём время :

;

(1.3)

Проверка размерности:

Вычислим:


2) Среднее ускорение движения тела определяется как отношение приращения скорости к промежутку времени , за которое это приращение произошло:

.

(1.4)

Находим скорости , в моменты времени и :

;	(1.5)
	(1.6)

Приращение скорости за время :

(1.7)

Таким образом, искомое среднее ускорение за время :

.

(1.8)

Проверка размерности: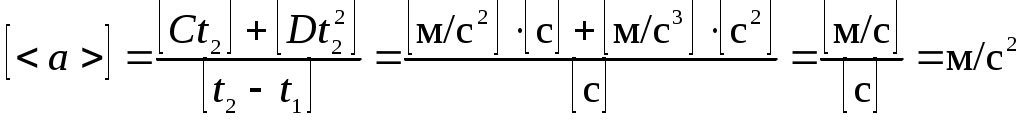

Вычислим, учитывая, что и :
.

Ответ: 1)  ; 2)  .

Задача 2 (№ 24)

Вентилятор вращается с частотой . После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки . Какое время прошло с момента выключения вентилятора до полной его остановки?

Дано: ; .	Решение При выключении начальная частота вращения равна , так как до выключения вентилятор вращался с постоянной частотой.

Угловое ускорение при равнопеременном замедленном вращении связанно с начальной и конечной угловыми скоростями соотношением

(2.1)

Так как , , то

(2.2)

где – частота вращения после полной остановки, об/с, .
Уравнение вращательного замедленного движения имеет вид

(2.3)

где – начальный угол вращения, рад, принимаем ;

– начальная угловая скорость (в проекции на ось вращения), ;

– угол вращения, рад, при оборотах, .
Мгновенная угловая скорость (в проекции на ось вращения):

(2.4)

Так как вентилятор остановился, .

Из уравнения (2.4) найдём время , которое прошло с момента выключения вентилятора до полной его остановки:

(2.5)

Найдём из (2.3) выражение для углового ускорения, с учетом того, что ; ; , :

; ; .

(2.6)

Подставим выражение (2.6) в уравнение (2.5), с учетом того, что ; :

(2.7)

Проверка размерности:

Вычислим:


Ответ:

Задача 3 (№ 44)

Трамвай, трогаясь с места, движется с ускорением . Через время после начала движения мотор выключается, и трамвай движется до остановки равнозамедленно. Коэффициент трения на всем пути . Найти наибольшую скорость движения трамвая и время движения трамвая. Каково его ускорение при равнозамедленном движении? Какое расстояние пройдет трамвай за время движения?

Дано: ; ; .	Решение Рассмотрим два участка движения трамвая: первый участок – участок с равноускоренным движением и второй участок – участок с равнозамедленным движением (рис. 3.1).
Рисунок 3.1

На первом участке на трамвай действуют силы: сила тяжести, сила реакции опоры, сила трения и сила тяги.

Запишем второй закон Ньютона для первого участка:

(3.1)

В проекции на оси и :

;	(3.2)
	(3.3)

Сила трения, с учетом уравнения (3.3)

(3.4)

Уравнение для равноускоренного движения трамвая:

(3.5)

где – путь, пройденный трамваем за время ;

– ускорение на первом участке.

Так как на первом участке трамвай трогается с места, то и , и уравнение (3.5) примет вид:

(3.6)

Наибольшей будет скорость в конце первого участка, т.к на втором участке скорость замедляется. Скорость в конце первого участка найдём из выражения для разности квадратов скоростей, с учетом того, что :

; .

(3.7)

Подставим выражение (3.6) в равенство (3.7), получим:

.

(3.8)

Проверка размерности:

Вычислим:

На втором участке на трамвай действуют силы: сила тяжести, сила реакции опоры и сила трения.

По второму закону Ньютона для второго участка имеем:

(3.9)

В проекции на оси и :

;	(3.10)
	(3.11)

Сила трения, с учетом уравнения (3.11)

(3.12)

Подставим выражение (3.12) в уравнение (3.10), найдём модуль ускорения при равнозамедленном движении

(3.13)

Вычислим:
.
Ускорение при равнозамедленном движении связанно с начальной и конечной скоростями соотношением

(3.14)

Учитывая, что на втором участке , , из выражения (3.13) найдём время движения трамвая от начала торможения до полной остановки:

(3.15)

Подставив выражения (3.8) и (3.13) в равенство (3.15), получим:

(3.16)

Расстояние, пройденное трамваем от начала торможения до полной остановки, с учетом , :

(3.17)

Подставив выражения (3.8) и (3.13) в равенство (3.17), получим:

(3.18)

Время движения трамвая

(3.19)

С учетом выражения (3.16)

(3.20)

Проверка размерности:

Вычислим:

За время движения трамвай пройдёт расстояние:

(3.21)

С учетом выражений (3.6) и (3.18):

(3.22)

Проверка размерности:

Вычислим:


Ответ: ; ; ;