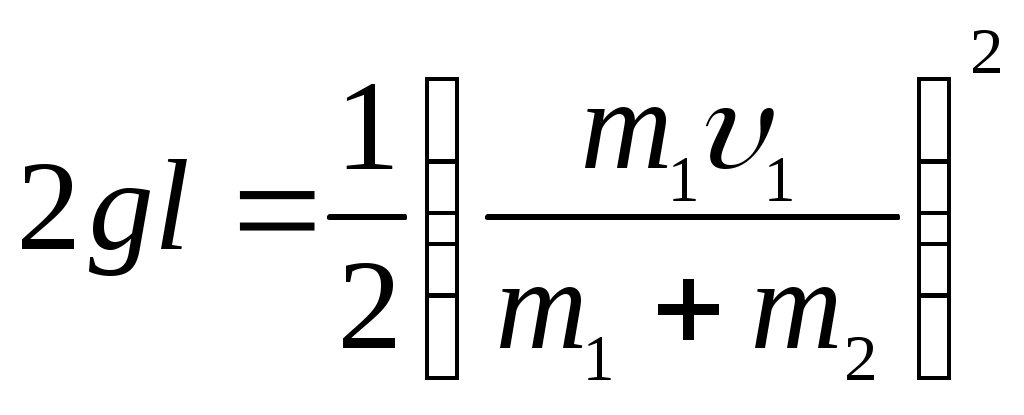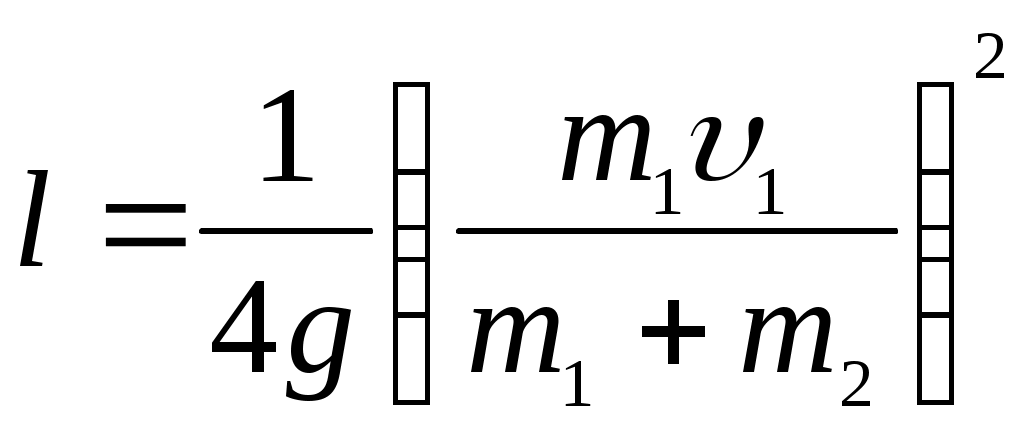Контрольная по ТОЭ. Решение_3713367. Решение 1) Мгновенная скорость есть первая производная пути по времени 1)

• Название: Решение 1) Мгновенная скорость есть первая производная пути по времени 1)
• Анкор: Контрольная по ТОЭ
• Дата: 05.03.2022
• Размер: 0.75 Mb.
• Имя файла: Решение_3713367.doc
• Тип: Решение; #384115
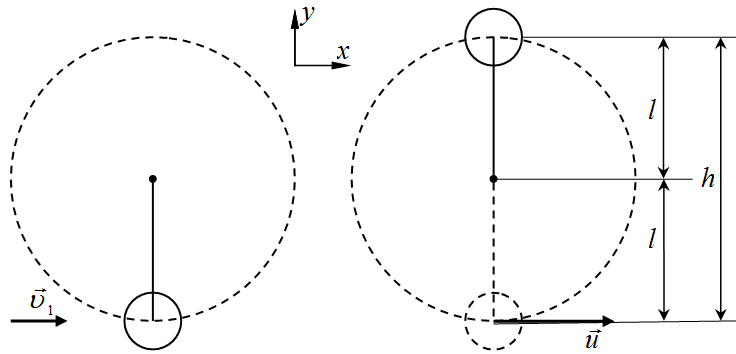
• страница: 2 из 2

Задача 4 (№ 64)

Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом жестком стержне, и застревает в нем. Масса пули , масса шара . Скорость пули . При каком предельном расстоянии от центра шара до точки подвеса стержня шар от удара пули поднимется до верхней точки окружности?

Дано: ; ; .

Решение

Рисунок 4.1

Система «пуля-шар» замкнута в проекции на ось (рис. 4.1). Применим закон сохранения импульса для системы «пуля-шар» в проекции на горизонтальное направление, считая положительным направление полёта пули.

(4.1)

где – скорость шара с застрявшей в нем пулей, м/с, .

– начальная скорость шара, м/с, .

Из выражения (4.1) найдём скорость движения шара вместе с пулей, с учетом того, что :

(4.2)

В нижней точке траектории шар вместе с пулей обладал кинетической энергией:

(4.3)

В верхней точке траектории шар вместе с пулей обладает потенциальной энергией:

(4.4)

За начальный уровень отсчета потенциальной энергии возьмём нижнюю точку траектории, тогда, как видно из рисунка (рис. 4.1):

(4.5)

По закону сохранения энергии:

(4.6)

Подставим выражения (4.3) и (4.5) в равенство (4.6):

(4.7)

Разделим левую и правую части уравнения (4.7) на :

(4.8)

С учетом выражения (4.2):

(4.9)

Из выражения (4.9) найдем предельное расстояние :

(4.10)

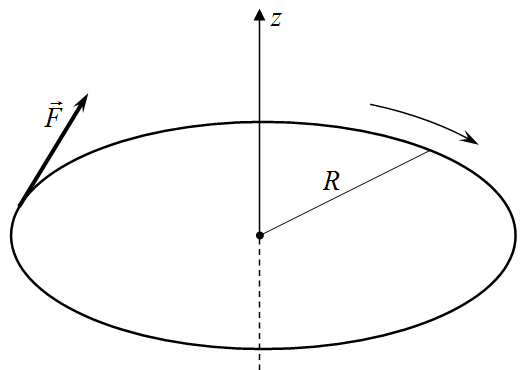
Проверка размерности: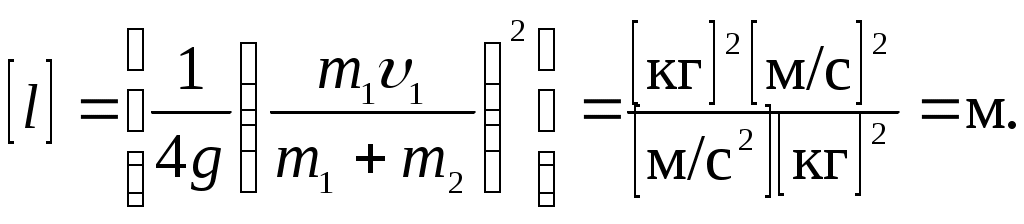

Вычислим:


Ответ: .

Задача 5 (№ 84)

Однородный диск радиусом и массой вращается вокруг оси, проходящей через его центр перпендикулярно к его плоскости. Зависимость угловой скорости вращения диска от времени дается уравнением , где . Найти касательную силу , приложенную к ободу диска. Трением пренебречь.

Дано: ; ; ;

Решение

Рисунок 5.1

Запишем основной закон динамики вращательного движения:

(5.1)

где – момент инерции диск,

– угловое ускорение, приобретаемое диском, под действием результищего момента сил.
На диск, по условию, действует касательная сила , приложенная к ободу диска. Момент этой силы, как видно из рисунка (рис. 5.1):

(5.2)

Значение углового ускорения найдем из уравнения угловой скорости, взяв первую производную по времени от

(5.3)

Момент инерции круглого однородного диска относительно оси, проходящей через его цент перпендикулярно к плоскости диска:

(5.4)

Подставим выражения (5.2), (5.3) и (5.4) в равенство (5.1), получим:

(5.5)

Отсюда касательная сила :

(5.6)

Проверка размерности:

Вычислим:


Ответ: .

Задача 6 (№ 104)

Шар диаметром и массой катится без скольжения по горизонтальной плоскости с частотой вращения . Найти кинетическую энергию шара.

Дано: ; ; .

Решение

Кинетическая энергия тела, участвующего одновременно в двух движениях, складывается из кинетической энергии поступательного и кинетической энергии вращательного движений:

(6.1)

При движении без проскальзывания угловая и линейная скорости связаны соотношением:

(6.2)

Угловая скорость и частота вращения связаны соотношением:

.

(6.3)

Из уравнения (6.2), с учетом (6.3), выразим линейную скорость шара, с учетом того, что :

(6.4)

Момент инерции однородного шара, ось вращения которого проходит через его центр, с учетом того, что :

(6.5)

Подставим выражения (6.3), (6.4) и (6.5) в уравнение (6.1):

(6.6)

Проверка размерности:


Вычислим:

Ответ:

Задача 7 (№ 124)

Частица массой совершает колебания вдоль оси по закону . При этом максимальное значение кинетической энергии частицы . Найти амплитуду колебаний.

Дано: ; ;

Решение
Чтобы найти амплитуду колебаний, воспользуемся формулой:

(7.1)

Скорость частицы – это первая производная от координаты по времени, т.е:

.

(7.2)

Так как , то максимальное значение скорости:

.

(7.3)

Подставим выражение (7.3) в уравнение (7.1).

(7.4)

Отсюда амплитуда колебаний:

(7.5)

Проверка размерности: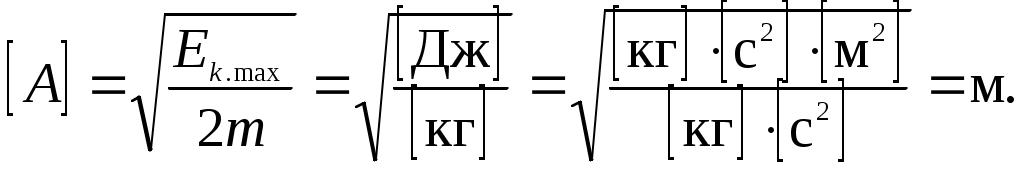

Вычислим:


Ответ:

Задача 8 (№ 144)

Определить скорость распространения волны в упругой среде, если разность колебаний двух точек среды, отстоящих друг от друга на , равна . Частота колебаний равна .

Дано: ; ; .

Решение
Разность фаз колебаний двух точек среды, расстояние между которыми равно определяется следующим соотношением:

(8.1)

Отсюда длина волны

(8.2)

Длина волны и частота колебаний связаны соотношением:

(8.3)

Отсюда скорость распространения волны в упругой среде

(8.4)

Подставим выражение (8.2) в равенство (8.4):

(8.5)

Проверка размерности:

Вычислим:


Ответ: