задачи по финансовой математике. задачи фин расчеты. Решение 1 Равные выплаты аннуитетными платежами, тогда все платежи, включая последний рассчитаем по формуле платежа ренты постнумерандо
 Скачать 17.53 Kb. Скачать 17.53 Kb.
|
|
1. Кредит в 1 000 000 у. е. выдан на 10 лет под 15% годовых. Чему равен последний платеж при возврате кредита методом равных выплат. Решение 1) Равные выплаты аннуитетными платежами, тогда все платежи, включая последний рассчитаем по формуле платежа ренты постнумерандо: 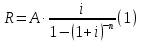 где A – современная стоимость ренты; i – ставка процента за период (год); n – количество периодов начисления (лет). 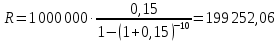 у.е. у.е.2) Равные выплаты основного долга (дифференцированные платежи). Ежегодно, включая последний месяц погашается по 100 000 у.е. основного долга и проценты. Сумма процентов за 10 год: (1 000 000 – 1 000 000/10×9)×0,15 = 24000 у.е. Итого последний платеж: 100 000 + 24 000 = 124 000 у.е. 2. На счет ежемесячно вносится по 9 240,772 у. е. в банк с процентной ставкой 13%. Определить, через какое время на счете будет 1 000 000 у. е Решение Формула расчета наращенной суммы ренты пренумерандо при ежегодном начислении процентов (m=1) и платежах несколько раз в год (p≠1) имеет вид: 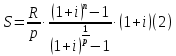 где S – наращенная стоимость потока платежей; n – количество периодов (лет); i – годовая ставка; R/p – аннуитетный платежа (R – сумма аннуитетов за год); p – количество платежей в год. Подставим значения и найдем n. 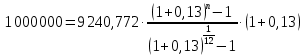 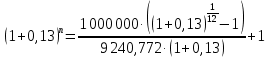 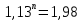 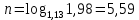 лет или 5 лет и 216 дней лет или 5 лет и 216 дней3. Для того чтобы начать свое дело, вам необходимы собственные средства в сумме 15 000 у. е. Уровень вашего текущего дохода позволяет вам откладывать на счет 800 у. е. ежемесячно. Через какое время вы накопите нужную сумму, если банк выплачивает по вкладам 9% годовых. Решение Используем формулу (2) 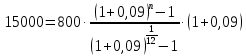 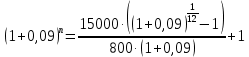 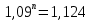 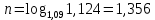 года или 1 год и 130 дней года или 1 год и 130 дней4. Определить ежеквартальные платежи для погашения кредита в 130 млн. у. е. за 24 лет при ставке 16%. Решение Для расчета ежеквартальных аннуитетных платежей используем формулу расчета современной стоимости ренты постнумерандо при ежегодном начислении процентов (m=1) и платежах несколько раз в год (p≠1): 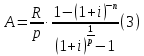 где S – наращенная стоимость потока платежей; n – количество периодов (лет); i – годовая ставка; R/p – аннуитетный платежа (R – сумма аннуитетов за год); p – количество платежей в год. Откуда ежеквартальный платеж составит: 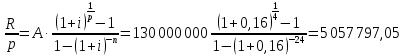 у.е. у.е.5. Компания планирует через 5 лет полностью заменить свой автопарк. Для этого она ежемесячно переводит на счет в банке по 6000 у. е. Банк начисляет по вкладам 12% годовых. Определить, какой суммой будет располагать компания на замену автопарка. Решение Используем формулу (2) для расчета наращенной суммы аннуитета пренумерандо при ежегодном начислении процентов (m=1) и платежах несколько раз в год (p≠1). Ежемесячный платеж R/p=6000 у.е., срок n=5 лет, количество платежей в год p=12. Наращенная сумма платежей для замены автопарка: 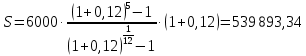 у.е. у.е.6. В банке размещена сумма в 140 000 у. е. на 3 года по учетной ставке 20% (сложные проценты). Определить накопленную сумму Решение наращенная сумма при неизменной ставке сложных процентов, начисляемых ежегодно, может быть определена по формуле: 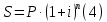 где i – годовая ставка сложных процентов; Р – первоначальная сумма вклада; n – период начисления в годах. Накопленная сумма составит: 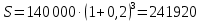 у.е. у.е.7. Родители решили, что для обучения в университете их сыну будет достаточно иметь по 11 000 у. е. в месяц. Определить, какую сумму им необходимо разместить в банке под 12% годовых с ежемесячным начислением, чтобы в течение 5 лет обучения их сын мог каждый месяц снимать со счета по 11 000 у. е. Решение Поскольку количество выплат и количество начислений в год равны (m=p=12), можно считать, что ставка i=12%/12=1%, а число выплат n=5*12=60. Тогда используем формулу расчета современной стоимости ренты постнумерандо: 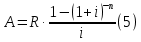 В банке необходимо будет разместить сумму: 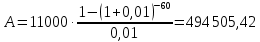 у.е. у.е. |
