ПГУПС МАТЕМАТИКА КР1. Решение а. б. Вычислим определитель разложением по элементам первой строки Задание 08
 Скачать 0.6 Mb. Скачать 0.6 Mb.
|
|
Задание 11.08 Написать уравнение плоскости в виде Решение  . . . .Разложим определитель по элементам первой строки:  Следовательно, получили уравнение плоскости: Задание 12.08 Даны вершины пирамиды SPMN. S(1, 0, 0); P(0, 4, 0); M(0, 0, 2); N(6, 9,2). Найти: 1) длину ребра SN; 2) уравнение ребра SN; 3) уравнение грани SPN; 4) площадь грани SPN; 5) уравнение высоты, опущенной из вершины S на грань PMN; 6) длину высоты, опущенной из вершины S на грань PMN; 7) угол между ребрами SP и SN (в градусах); 8) угол между ребром SP и гранью PMN (в градусах); 9) объем пирамиды. В ответах надо приводить уравнения плоскостей и прямых в виде Аx+ Вy + Cz + D = 0 и 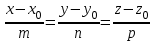 . Все вычисления проводить с двумя знаками после запятой. . Все вычисления проводить с двумя знаками после запятой.Решение 1.Длину ребра 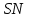 найдём по формуле расстояния между двумя точками: найдём по формуле расстояния между двумя точками: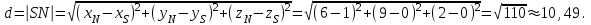 2.Уравнеие ребра 2.Уравнеие ребра 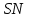 запишем в каноническом виде: запишем в каноническом виде: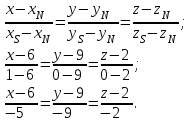 где 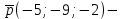 направляющий вектор прямой. направляющий вектор прямой.3.Уравнение грани 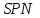 находим по следующей формуле: находим по следующей формуле: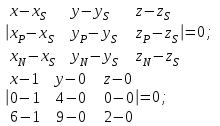 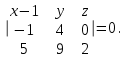 Разложим определитель по элементам первой строки: 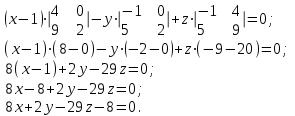 4.Найдём площадь грани 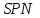 . .Треугольник 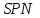 является половиной параллелограмма, построенного на векторах является половиной параллелограмма, построенного на векторах 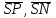 , тогда , тогда 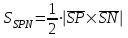 . . 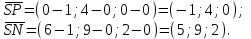 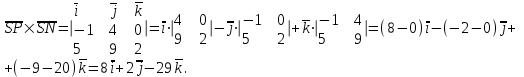 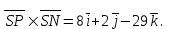 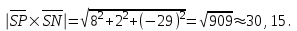 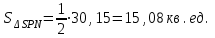 5.Найдём уравнение высоты, опущенной из вершины 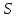 на грань на грань 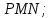 Если прямая проходит через точку S(1; 0; 0)  и параллельна нормальному вектору и параллельна нормальному вектору 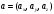 к грани к грани 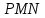 , то ее уравнение определяется следующим выражением: , то ее уравнение определяется следующим выражением: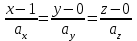 Нормальный вектор 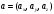 ищем из следующего выражения: ищем из следующего выражения: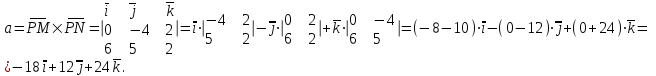 Тогда координаты нормального вектора плоскости Тогда координаты нормального вектора плоскости 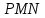 : : 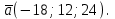 И уравнение высоты, опущенной из вершины S на грань 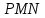 примет окончательный вид: примет окончательный вид: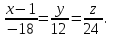 . .6.Найдём длину высоты, опущенной из вершины 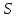 на грань на грань 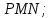 Расстояние 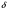 от точки от точки 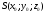 до плоскости до плоскости 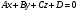 определяется выражением: определяется выражением: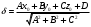 Но для начала найдём уравнение грани 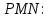 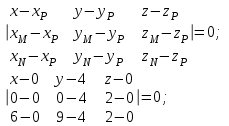 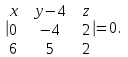 Разложим определитель по элементам первого столбца: 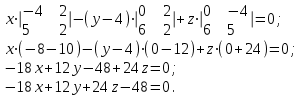 Или для нашего случая 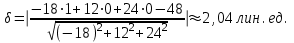 7.Найдём угол между рёбрами 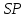 и и 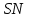 (в градусах); (в градусах);Угол между рёбрами будем искать как угол между двумя направляющими векторами данных прямых. Для прямой 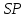 координаты направляющего вектора: координаты направляющего вектора: 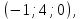 а для прямой а для прямой 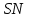 координаты направляющего вектора: координаты направляющего вектора: 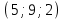 . Тогда по формуле, находим . Тогда по формуле, находим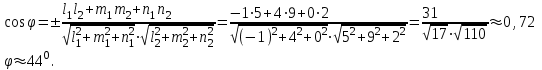 8.Найдём угол между ребром 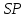 и гранью и гранью 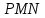 (в градусах); (в градусах);Направляющий вектор прямой 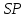 имеет координаты имеет координаты 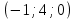 , а координаты нормального вектора плоскости , а координаты нормального вектора плоскости 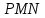 следующие следующие 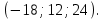 Тогда угол найдём по следующей формуле: Тогда угол найдём по следующей формуле: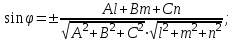 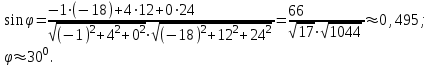 9.Найдём объём пирамиды, для этого рассмотрим векторы 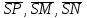 на которых построена данная пирамида: на которых построена данная пирамида: 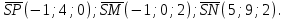 Тогда, 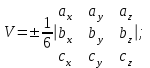 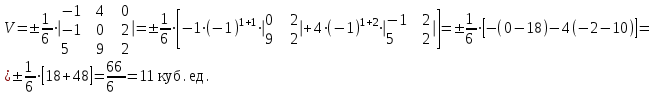 Сделаем рисунок. Сделаем рисунок.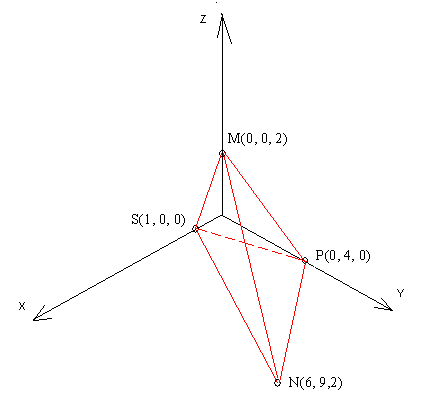 Задание 13.08 Вычислить комплексное число 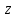 и найти его модуль и найти его модуль 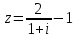 . .Решение Умножим числитель и знаменатель на сопряжённый знаменателю множитель 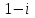 : : 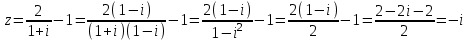 . .Получили комплексное число в алгебраической форме: 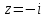 , у которого , у которого 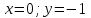 . Модуль найдём по формуле: . Модуль найдём по формуле: 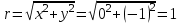 . .Задание 14.08 Дано комплексное число 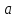 . Требуется: . Требуется:а) записать число 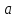 в алгебраической, тригонометрической и показательной формах; в алгебраической, тригонометрической и показательной формах;б) изобразить 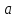 на комплексной плоскости; на комплексной плоскости;в) вычислить 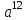 ; ;г) найти все корни уравнения 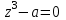 ; ;д) вычислить произведение полученных корней; е) составить квадратное уравнение с действительными коэффициентами, корнем которого является 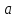 : : 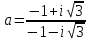 . .Решение а) Умножим числитель и знаменатель на сопряжённый знаменателю множитель 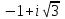 , а также умножим числитель и знаменатель на сопряжённый числителю множитель , а также умножим числитель и знаменатель на сопряжённый числителю множитель 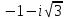 : :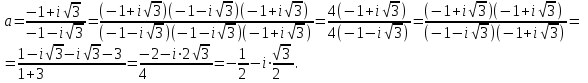 - алгебраическая форма комплексного числа. - алгебраическая форма комплексного числа.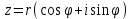 , где , где 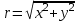 , у нас , у нас 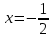 , , 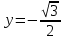 . .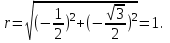 Анализируем аргумент, чтобы определить угол. Так как Анализируем аргумент, чтобы определить угол. Так как 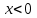 и и 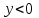 , то , то 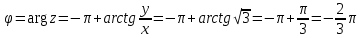 . .Окончательно, получим тригонометрическую формулу данного числа: 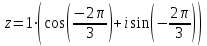 . .Показательная форма комплексного числа: 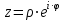 , тогда , тогда 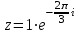 б) Изобразим это число на комплексной плоскости: 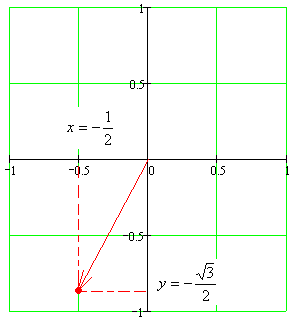 в) Применим формулу: 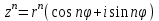 . .Мы нашли тригонометрическую форму заданного числа 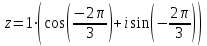 , тогда , тогда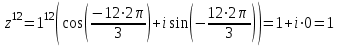 . .г) Найдём корни уравнения 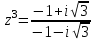 . . 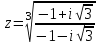 . .Для извлечения корня применим формулу: 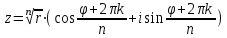 , где , где 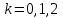 . .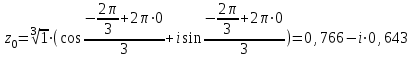 , ,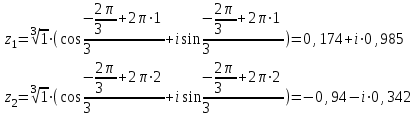 д) Вычислим произведение полученных корней. 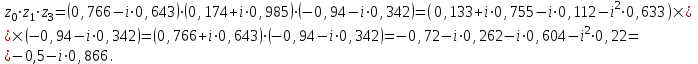 е) Составим квадратное уравнение с действительными коэффициентами, корнем которого является е) Составим квадратное уравнение с действительными коэффициентами, корнем которого является 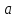 : : 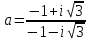 . .Квадратное уравнение имеет вид: 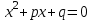 . Вспоминая теорему Виета, запишем . Вспоминая теорему Виета, запишем 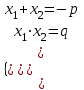 Один из корней 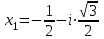 , значит второй равен , значит второй равен 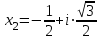 . Тогда, . Тогда,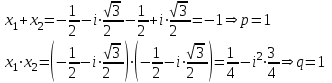 Тогда, квадратное уравнение примет вид: 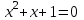 . .Задание 15.08 Для заданной функции найти точки разрыва, если они существуют, и построить график. 8. 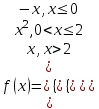 решение: функции 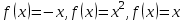 являются непрерывными функциями на своих областях задания и могут иметь разрыв только в точках перехода от одной функции в другую. Проверим функцию в точке являются непрерывными функциями на своих областях задания и могут иметь разрыв только в точках перехода от одной функции в другую. Проверим функцию в точке 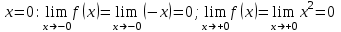 . Так как значение функции совпадают то функция непрерывна в этой точке. . Так как значение функции совпадают то функция непрерывна в этой точке.В точке 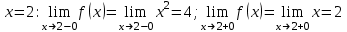 . Так как значение функции не совпадают но конечны то функция в этой точке имеет разрыв первого рода в виде скачка. . Так как значение функции не совпадают но конечны то функция в этой точке имеет разрыв первого рода в виде скачка.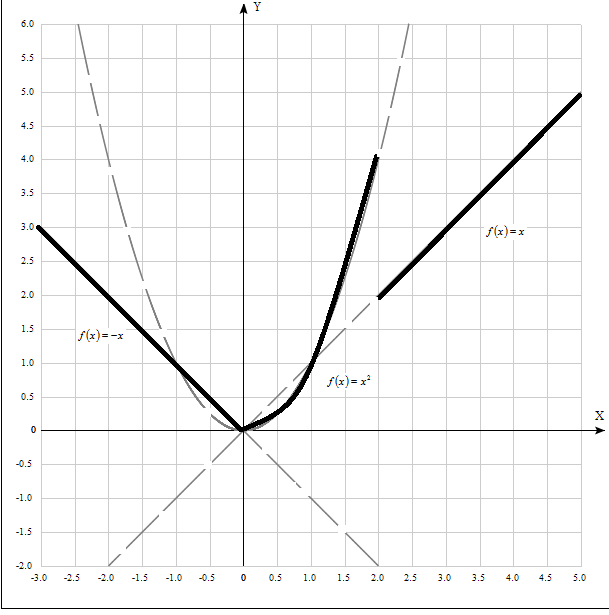 Задание 16.08 Найти пределы функций. 8. 1) 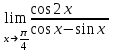 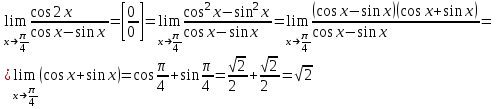 2) 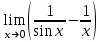 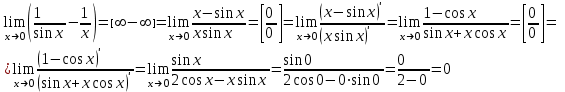 3) 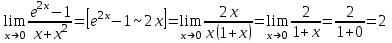 4) 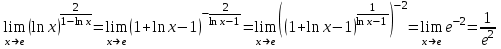 5) 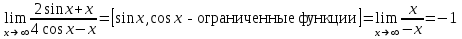 Задание 17.08 Найти производные функций 8. 1) 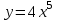 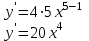 2) 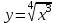 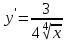 3) 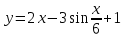 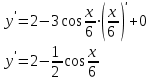 4) 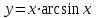 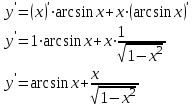 5) 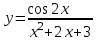 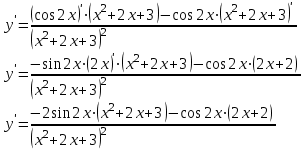 Задание 18.08 Найти производные функций. 8. 1) 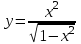 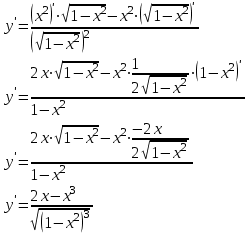 2) 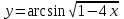 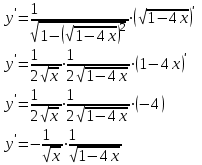 3) 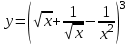 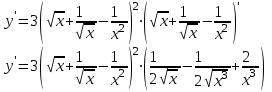 4) 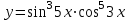 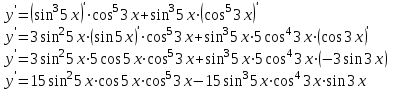 5) 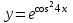 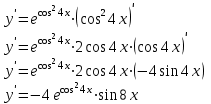 6) 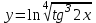 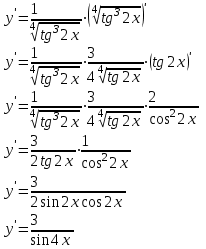 Задание 19.08 Найти производные функций. 8. 1) 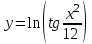 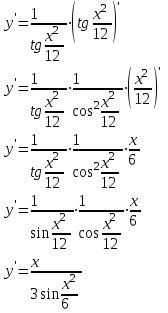 2) 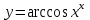 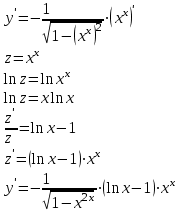 3) 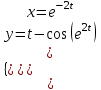 найдем производную по формуле: 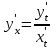 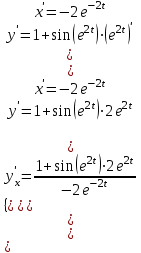 4) 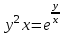 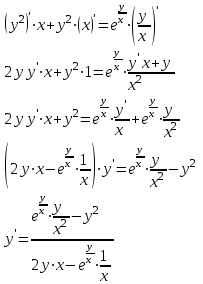 |
