ПГУПС МАТЕМАТИКА КР1. Решение а. б. Вычислим определитель разложением по элементам первой строки Задание 08
 Скачать 0.6 Mb. Скачать 0.6 Mb.
|
|
Задание 20.08 Найти экстремумы и промежутки монотонности функций; построить графики функций. 8. 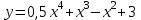 решение: используем первую производную: Проведем исследование функции с помощью первой производной, то есть найдем точки экстремума функции и интервалы возрастания и убывания. 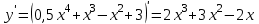 Найдем точки, в которых первая производная равна нулю или не существует. Функция 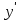 равна нулю при равна нулю при 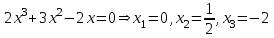 . .Отметим на области определения критические точки. Проверим знаки функции в полученных областях. Так как при переходе точек 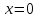 функция меняет знак с плюса на минус, то в этой точке имеет максимум, а при переходе точки функция меняет знак с плюса на минус, то в этой точке имеет максимум, а при переходе точки 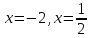 функция меняет знак с минуса на плюс, то она имеет минимум. функция меняет знак с минуса на плюс, то она имеет минимум.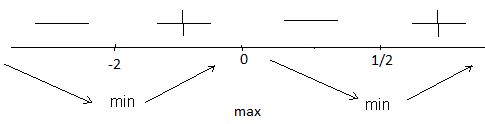 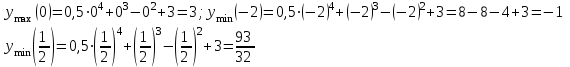 Функция возрастает на промежутках 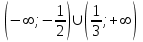 . Убывает на промежутке . Убывает на промежутке 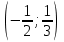 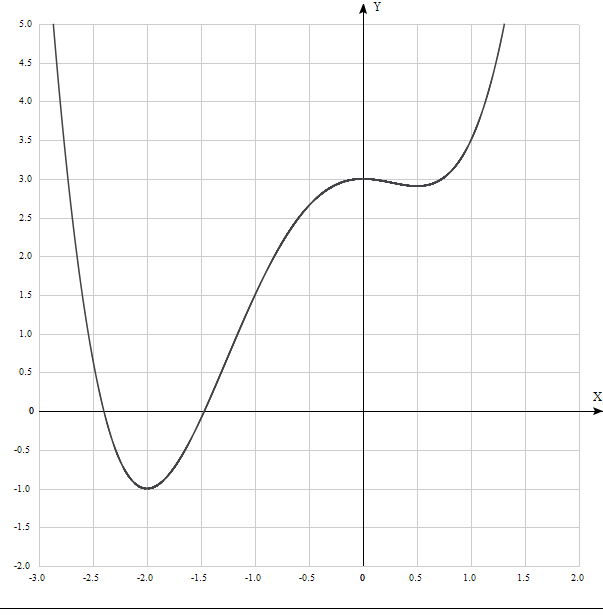 Задание 21.08 Исследовать функции методами дифференциального исчисления и построить их графики. 8. 1) 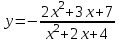 ; ; Найдем ОДЗ и точки разрыва функции. Функция определенна всюду на числовой оси 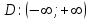 . Исследуем функцию на концах промежутка. . Исследуем функцию на концах промежутка.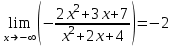 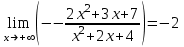 Найдём точки пересечения графика функции с осями координат. 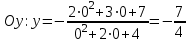 , точка (0; , точка (0; 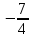 ) )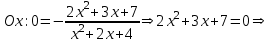 нет точек пересечения. нет точек пересечения.Заметим, что перед построением графика полезно установить, не является ли данная функция четной или нечетной. 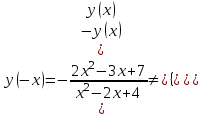 Значит функция общего вида. Проведем исследование функции с помощью первой производной, то есть найдем точки экстремума функции и интервалы возрастания и убывания. 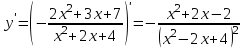 Найдем точки, в которых первая производная равна нулю или не существует. Функция 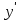 равна нулю при равна нулю при 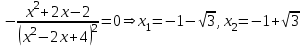 . .Отметим на области определения критические точки. Проверим знаки функции в полученных областях: Так как при переходе точек 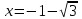 функция меняет знак с плюса на минус, то в этой точке имеет максимум, а при переходе точки функция меняет знак с плюса на минус, то в этой точке имеет максимум, а при переходе точки 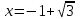 функция меняет знак с минуса на плюс, то она имеет минимум. функция меняет знак с минуса на плюс, то она имеет минимум.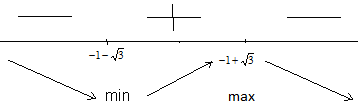 Функция возрастает на промежутках 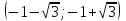 . .Убывает на промежутке 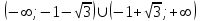 . .Найдем асимптоты графика функции: а) вертикальные и горизонтальные 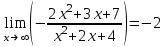 - горизонтальная асимптота - горизонтальная асимптота 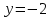 . .вертикальных асимптот нет. b) наклонные. Общий вид 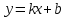 Где 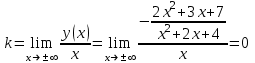 То есть наклонных асимптот нет. На основании проведённого исследования построим график функции. 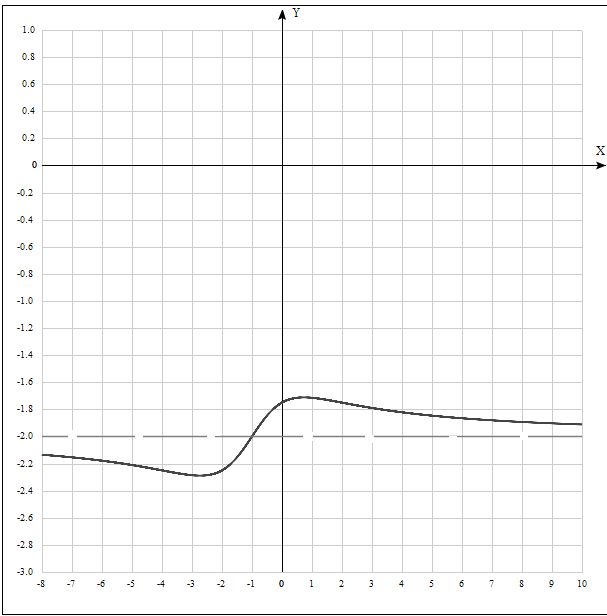 2) 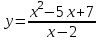 Найдем ОДЗ и точки разрыва функции. Функция определенна всюду на числовой оси 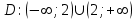 . Исследуем функцию на концах промежутка. . Исследуем функцию на концах промежутка.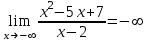 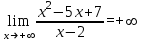 Найдём точки пересечения графика функции с осями координат. 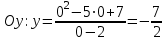 , точка (0; , точка (0; 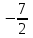 ) )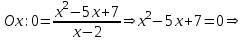 нет точек пересечения. нет точек пересечения.Заметим, что перед построением графика полезно установить, не является ли данная функция четной или нечетной. 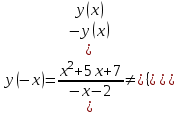 Значит функция общего вида. Проведем исследование функции с помощью первой производной, то есть найдем точки экстремума функции и интервалы возрастания и убывания. 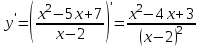 Найдем точки, в которых первая производная равна нулю или не существует. Функция 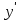 равна нулю при равна нулю при 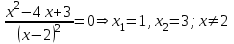 . .Отметим на области определения критические точки. Проверим знаки функции в полученных областях: Так как при переходе точек 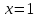 функция меняет знак с плюса на минус, то в этой точке имеет максимум, а при переходе точки функция меняет знак с плюса на минус, то в этой точке имеет максимум, а при переходе точки 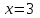 функция меняет знак с минуса на плюс, то она имеет минимум. функция меняет знак с минуса на плюс, то она имеет минимум.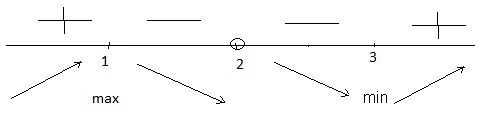 Функция возрастает на промежутках 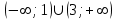 . .Убывает на промежутке 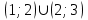 . .Найдем асимптоты графика функции: а) вертикальные и горизонтальные 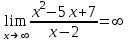 - горизонтальных асимптот нет. - горизонтальных асимптот нет.вертикальная асимптота 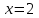 . .b) наклонные. Общий вид 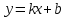 Где 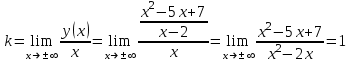 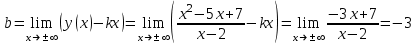 То есть наклонная асимптота 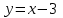 . .На основании проведённого исследования построим график функции. 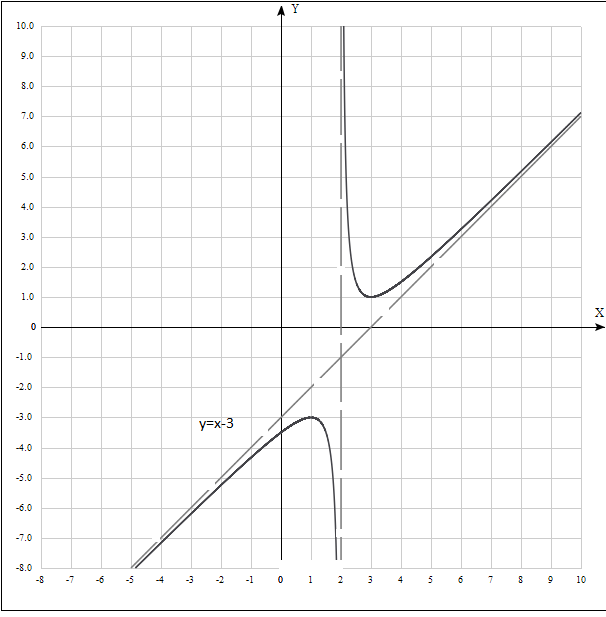 |
