ПГУПС МАТЕМАТИКА КР1. Решение а. б. Вычислим определитель разложением по элементам первой строки Задание 08
 Скачать 0.6 Mb. Скачать 0.6 Mb.
|
|
Контрольная работа 1 Задание 1.08 Вычислить определители. а) 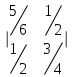 , б) , б)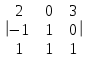 . .Решение а) 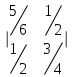 . .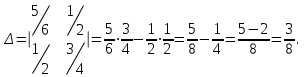 б) 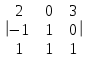 . .Вычислим определитель разложением по элементам первой строки: 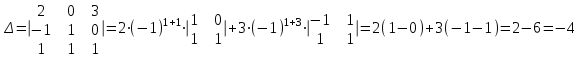 . .Задание 2.08 Решить систему линейных уравнений методом Гаусса и по формулам Крамера. Сделать проверку. 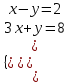 Решение 1) метод Гаусса. Умножим первую строку на (-3) и сложим со второй строкой: 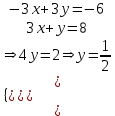 , найдём , найдём 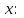 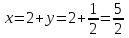 . .Проверка: 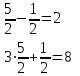 Ответ: 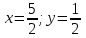 . .2)Формулы Крамера имеют вид: 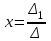 , , 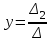 . .Найдём определитель системы: 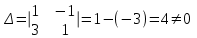 . .Найдём вспомогательные определители системы 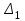 и и 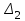 : :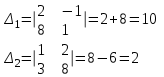 Тогда, 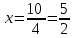 , , 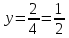 . .Задание 3.08 Решить систему линейных уравнений тремя методами: а) по формулам Крамера; б) методом Гаусса; в) с помощью обратной матрицы. 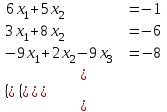 Решение а) Формулы Крамера имеют вид: 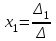 , , 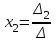 , , 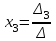 . .Найдём главный определитель системы 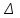 : : 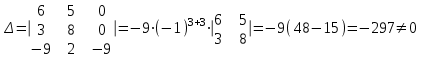 Найдём вспомогательные определители 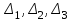 : :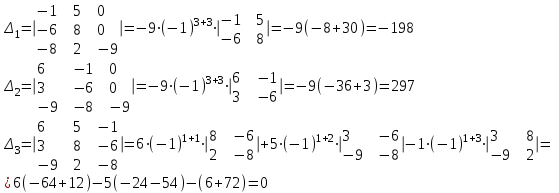 Тогда, 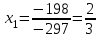 , , 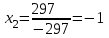 , , 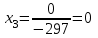 . .Проверка: 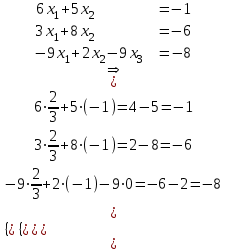 б) метод Гаусса: 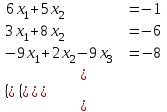 Запишем систему в виде расширенной матрицы: 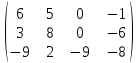 Меняем местами первую и вторую строку: 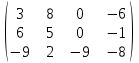 Первую строку умножим на -2 и сложим со второй строкой, результат во второй строке, первую строку умножим на 3 и сложим с третьей строкой, результат в третьей строке. 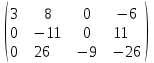 Вторую строку разделим на 11: 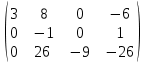 Из второй строки найдём 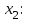 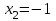 . .Из третьей строки найдём 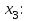 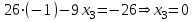 . .Из первой строки найдём 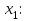 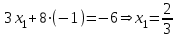 . .Ответ: 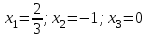 . .в) с помощью обратной матрицы: 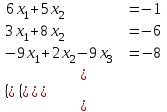 Решение ищем в виде 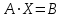 , откуда , откуда 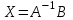 . . Вводим обозначения: 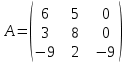 , , 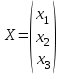 , , 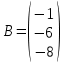 . .Найдём обратную матрицу 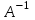 , для этого найдём алгебраические дополнения: , для этого найдём алгебраические дополнения: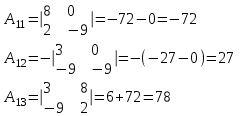 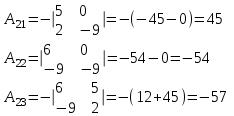 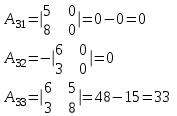 Запишем обратную матрицу: 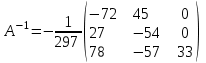 . .Найдём 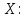 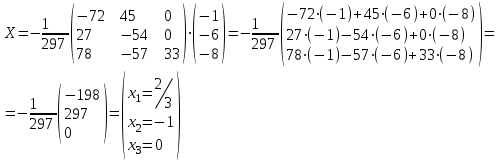 Задание 4.08 Исследовать (по теореме Кронекера - Капелли) совместность и решить систему линейных уравнений. 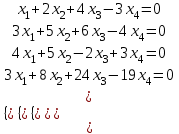 Решение Теорема Кронекера - Капелли гласит, для того, чтобы система была совместна, необходимо и достаточно, чтобы ранг матрицы А системы равнялся рангу расширенной матрицы В, т.е. 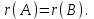 Покажем это. Составим расширенную матрицу системы. Покажем это. Составим расширенную матрицу системы.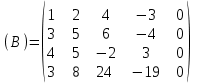 Очевидно, ранг матрицы системы и ранг расширенной матрицы не превосходит числа их строк, т.е. 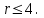 С другой стороны, минор второго порядка, расположенный в верхнем левом углу, отличен от нуля: С другой стороны, минор второго порядка, расположенный в верхнем левом углу, отличен от нуля: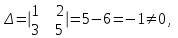 т.е. ранг системы т.е. ранг системы 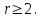 Подвергнем расширенную матрицу следующим преобразованиям: умножим первую строку на 3: 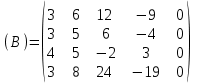 Первую строку вычтем из 2-ой строки, а первую строку разделим на 3: 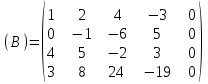 Первую строку умножим на 4: 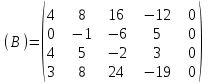 Вычли первую строку из третьей строки и восстановили её: 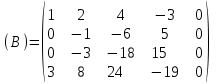 Первую строку умножим на 3: 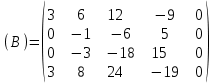 Вычли первую строку из четвёртой и восстановили её: 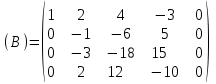 Умножим вторую строку на (-3): 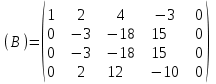 Вычли вторую строку из третьей строки и восстановили её: 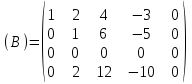 Умножим вторую строку на 2: 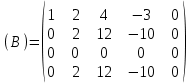 Вычли вторую строку из четвёртой строки и восстановили её: 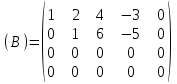 Получили две линейно независимые строки. Видим, что ранг 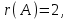 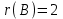 . . Следовательно, система имеет бесчисленное множество решений и сделаем последний шаг, умножим вторую строку на (-2) и сложим с первой строкой: 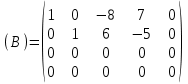 Запишем ответ: 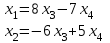 , где , где 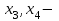 свободные члены. свободные члены.Задание 5.08 При каких А и В система имеет бесчисленное множество решений? Найти эти решения. 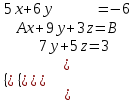 Решение Система имеет бесчисленное множество решений, когда главный определитель системы равен нулю, но по крайней мере найдётся один элемент, минор которого отличен от нуля. 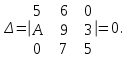 Раскроем данный определитель по элементам первой строки: 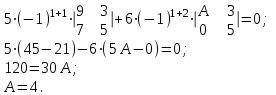 При А=4 – главный определитель системы равен нулю. Запишем расширенную матрицу системы с учётом того, что А=4. 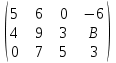 Умножим первую строку на 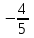 и сложим со второй строкой, запишем во вторую строку. и сложим со второй строкой, запишем во вторую строку.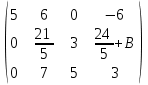 Для того, чтобы система имела бесчисленное множество решений, сделаем так, чтобы вторая и третья строки стали одинаковыми. Умножим строку три на 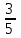 . .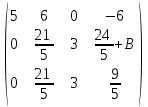 А также, 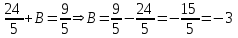 , т.е. примем , т.е. примем 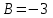 . .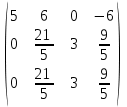 Третью строку можем убрать: 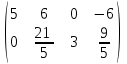 Первую строку разделим на 5: 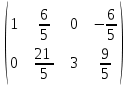 Умножим вторую строку на 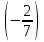 и сложим с первой строкой: и сложим с первой строкой: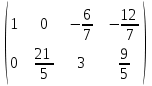 Вторую строку разделим на 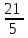 : :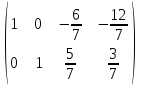 Тогда, 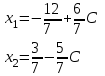 , где С – любое число. , где С – любое число.Следовательно, при 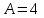 и и 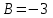 , система имеет бесчисленное множество решений. , система имеет бесчисленное множество решений.Задание 6.08 Даны векторы 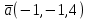 , , 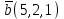 . Найти . Найти 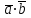 , , 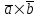 и длину и длину 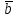 . .Решение Найдём скалярное произведение 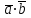 : :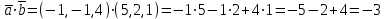 . .Найдём векторное произведение: 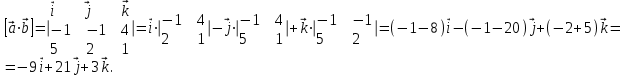 Найдём длину Найдём длину 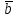 : :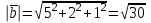 . .Задание 7.08 Написать уравнение плоскости, проходящей через точки 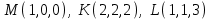 в виде в виде 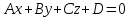 . .Решение. 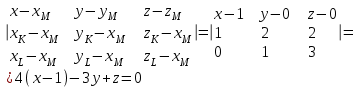 или 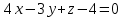 Задание 8.08 Даны векторы 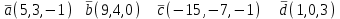 Вычислить 1) координаты вектора 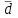 в базисе в базисе 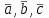 2) 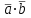 3) 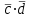 4) 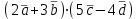 5) 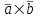 6) 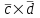 7) 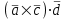 Решение. 1)  Найдем координаты вектора из системы уравнений 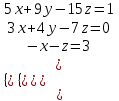 Решим систему методом Крамера 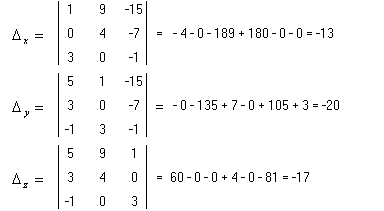 Тогда получаем 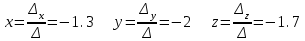 Тогда искомое разложение принимает вид 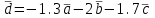 2) 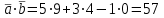 3) 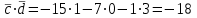 4) 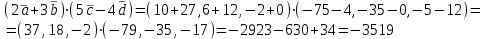 5) 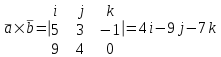 6) 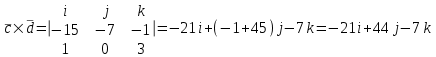 7) 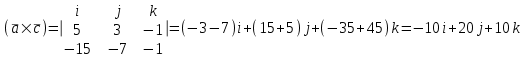 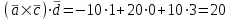 Задание 9.08 Написать уравнение прямой, проходящей через точки А и В в виде 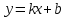 , построить эту прямую: , построить эту прямую:  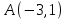 , , 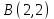 . .Решение 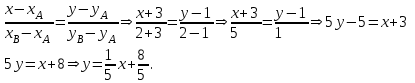 . .Сделаем рисунок. 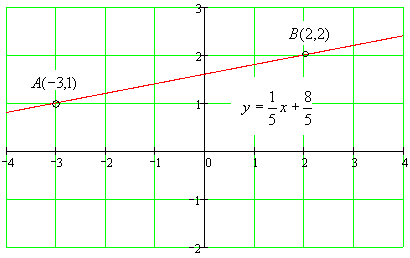 Задание 10.08 Даны вершины треугольника ABC. A(1, 3); B(-5, 2); C(-3, 5). Найти: 1) длину стороны AB; 2) уравнения стороны AB; 3) длину медианы AM; 4) уравнение медианы AM; 5) уравнение высоты BH; 6) длину высоты BH; 7) площадь треугольника; 8) угол BAC (в градусах); 9) уравнения прямой параллельной стороне ВС и проходящей через точку А. В ответах надо приводить уравнения прямых в виде y = kx+b. Все вычисления проводить с двумя знаками после запятой. Решение 1.Длину стороны АВ найдём по формуле расстояния между двумя точками: 2.Уравнение стороны АВ запишем как уравнение прямой, проходящей через две заданные точки:  3.Найдём длину медианы АМ, но предварительно найдём координаты точки М. Так как медиана делит сторону, на которую она опущена пополам, то используя координаты деления отрезка пополам, запишем: Тогда, найдём длину медианы: 4.Запишем уравнение медианы  5.Высота Найдём уравнение прямой АС:  Для прямой АС угловой коэффициент равен 6.Найдём длину высоты Координаты т.  7. Площадь треугольника АВС найдём по следующей формуле: 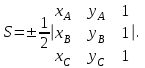  8.Угол ВАС найдём по следующей формуле: Угол ВАС – это угол между двумя прямыми АВ и АС, угловой коэффициент для прямой АВ:  9.Запишем уравнение стороны ВС:  Угловой коэффициент для прямой ВС:  Сделаем рисунок. 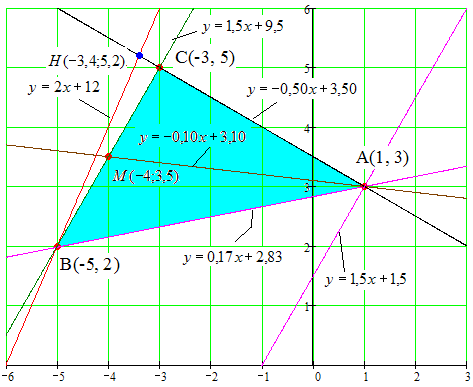 |
