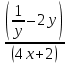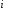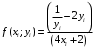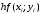Контрольная работа выс мат. готовая контрольная работа 2. Решение а Ответ б Тогда Ответ
 Скачать 234.31 Kb. Скачать 234.31 Kb.
|
|
Контрольный блок задач М6. 6.01-6.10 (а, б). Решить задачу Коши. 6.01. а)  б) Решение: а)  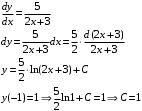 Ответ: 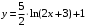 б) 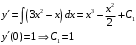 Тогда 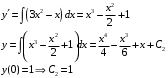 Ответ: 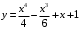 6.11-6.20. Составить таблицу численного решения методом Эйлера дифференциального уравнения 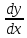 =f(x,y) при начальном условии y(x0)=y0 на отрезке [a,b] c шагом h. По полученным данным построить интегральную кривую. =f(x,y) при начальном условии y(x0)=y0 на отрезке [a,b] c шагом h. По полученным данным построить интегральную кривую.
Решение: Найдем каждое последующее значение по формуле 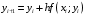 Получим рассчетную таблицу:
Отложив на оси абсцисс значения 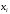 , а на оси ординат – значения , а на оси ординат – значения 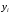 , получим интегральную кривую: , получим интегральную кривую: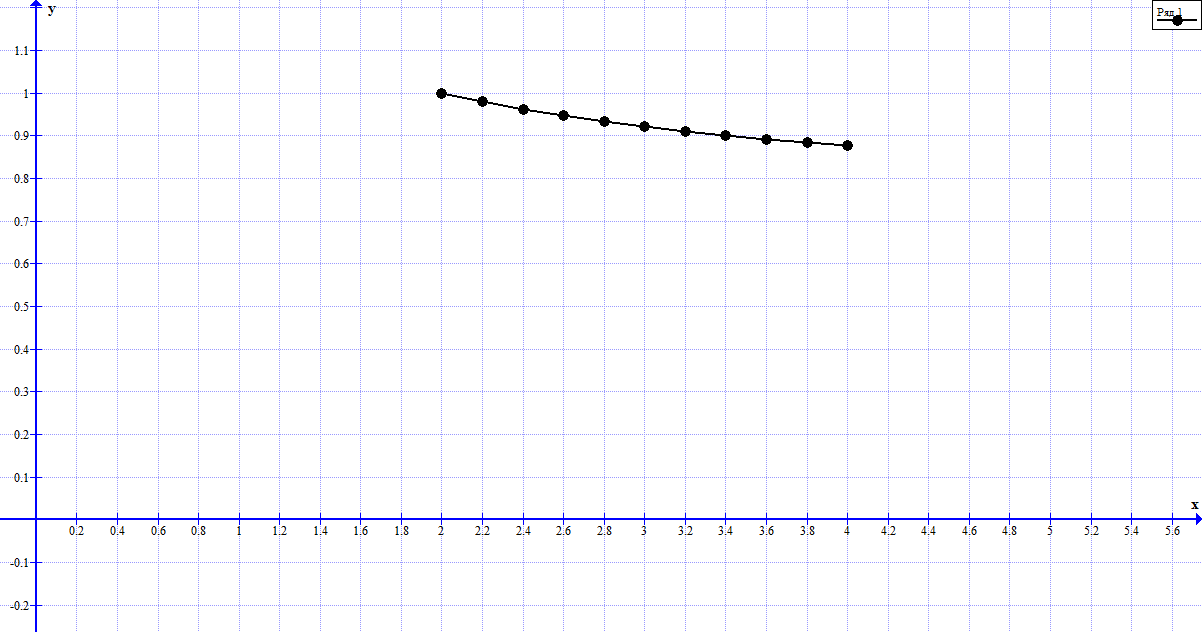 6.21-6.30 (а, б, в). Найти общие решения однородных дифференциальных уравнений. 6.21. а) б) в) Решение: а) Характеристическое уравнение: 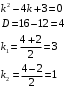 Тогда 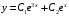 Ответ: 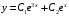 б) Характеристическое уравнение: 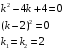 Тогда 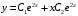 Ответ: 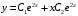 в) Характеристическое уравнение: 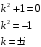 Тогда 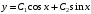 Ответ: 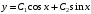 6.31-6.40 (а, б). Найти общее решение дифференциальных уравнений. 6.31. a) (2y+1)sin2xdy+5y dx=0; б) ysinx+ycosx=2x. Решение: (2y+1)sin2xdy+5y dx=0; 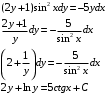 Ответ: Общий интеграл 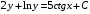 б) ysinx+ycosx=2x. 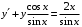 Выполним замену 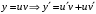 Получим: 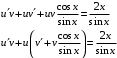 Положим 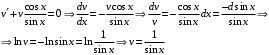 Тогда 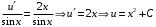 Тогда 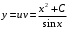 Ответ: 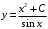 6.41-6.50 (а, б). Решить задачу Коши. 6.41. а) y=(2x+3)/(4y+5), y(0)=1; б) (y–2x+3)dx+(x–y+3)dy=0, y(1)=2. Решение: а) y=(2x+3)/(4y+5), y(0)=1; 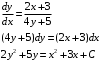 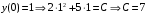 Ответ: 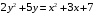 б) (y–2x+3)dx+(x–y+3)dy=0, y(1)=2. Решение: 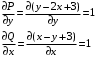 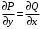 – имеем уравнение в полных дифференциалах. – имеем уравнение в полных дифференциалах.Получим систему: 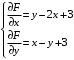 Из первого уравнения 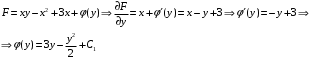 Откуда 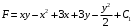 Тогда общий интеграл уравнения имеет вид: 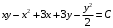 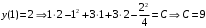 Ответ: 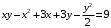 6.51-6.60 (а, б). Найти общие решения дифференциальных уравнений. 6.51. а) y=y/x, б) y+4y=1/sin(2x). Решение: а) y=y/x, Выполним замену: 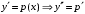 Получим: 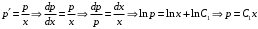 Тогда 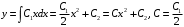 Ответ: 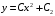 б) y+4y=1/sin(2x). Характеристическое уравнение: 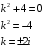 Тогда общее решение однородного уравнения 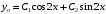 Положим 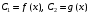 Тогда 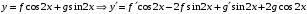 Положим 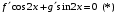 Тогда 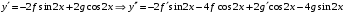 Подставим найденные значения в исходное уравнение: 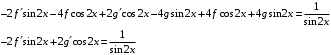 Вместе с уравнением (*) получим систему: 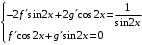 Из второго уравнения 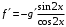 Подставим в первое уравнение: 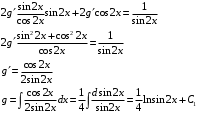 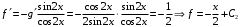 Тогда 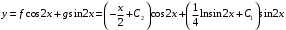 Ответ: 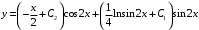 6.61-6.70 (а, б). Решить задачу Коши. 6.61. а) y+4y+4y= 4x2+4x+6, у(0)=1, y(0)=0. б) y–5y+6y= –e2x, у(0)=0, y(0)=0. Решение: а) y+4y+4y= 4x2+4x+6, у(0)=1, y(0)=0 Характеристическое уравнение: 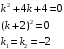 Тогда общее решение однородного уравнения 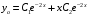 Частное решение будем искать в виде 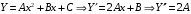 Подставим найденные значения в исходное уравнение: 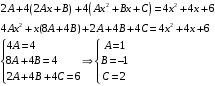 Тогда 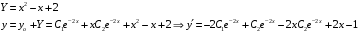 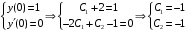 Ответ: 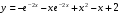 б) y–5y+6y= –e2x, у(0)=0, y(0)=0. Характеристическое уравнение: 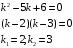 Тогда общее решение однородного уравнения 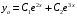 Частное решение будем искать в виде 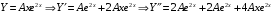 Подставим найденные значения в исходное уравнение: 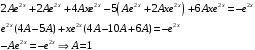 Тогда 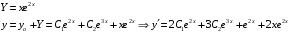 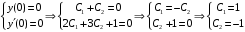 Ответ: 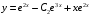 6.71-6.80. Найти общее решение дифференциального уравнения. 6.71. y–2y=(x+1)e2x+2xe3x. Решение: Характеристическое уравнение: 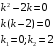 Тогда общее решение однородного уравнения 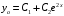 Частное решение будем искать в виде 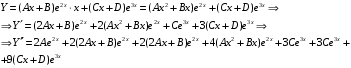 Подставим найденные значения в исходное уравнение: 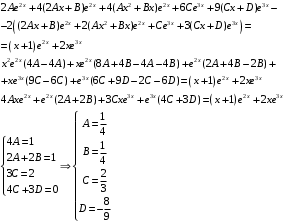 Тогда 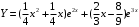 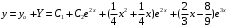 Ответ: 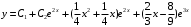 6.81. Локомотив уменьшил скорость с 10 м/с до 5 м/с за 60 с. Полагая силу торможения пропорциональной квадрату скорости движения локомотива, определить время, необходимое для достижения скорости 2 м/с. Решение: По условию, сила торможения 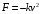 , где , где 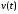 – скорость, – скорость, 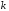 – коэффициент пропорциональности. – коэффициент пропорциональности.С другой стороны, 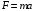 , где , где 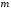 – масса, – масса, 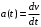 – ускорение. – ускорение.Получим: 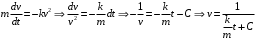 С другой стороны, по условию, 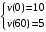 Откуда 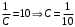 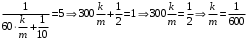 Тогда 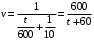 Найдем момент времени, при котором скорость локомотива равна 2 м/с: 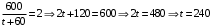 Ответ: 240 с. 6.91-6.100. Найти общее решение системы линейных дифференциальных уравнений с постоянными коэффициентами. 6.91. 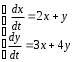 Решение: Из первого уравнения 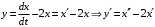 . .Подставим во второе уравнение: 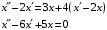 Характеристическое уравнение: 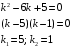 Тогда 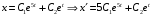 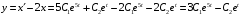 Ответ: 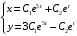 |