Физика. Решение а уравнение ac б Найдем длину высоты, как расстояние от точки a до прямой bc
 Скачать 236.86 Kb. Скачать 236.86 Kb.
|
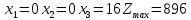 №7
Составим математическую модель задачи 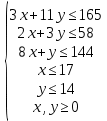 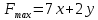 Строим область D, находя пересечение полуплоскостей, каждая из которых задается одним из неравенств системы 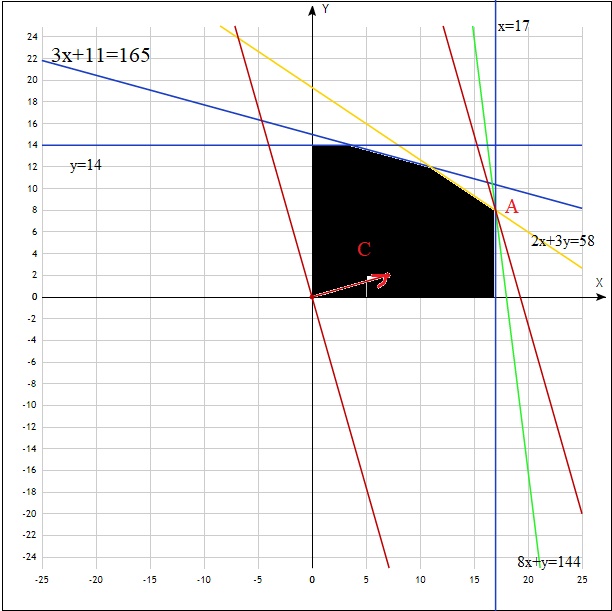 Находим градиент целевой функции- вектор 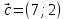 , и откладываем его от начала координат. , и откладываем его от начала координат.Строим линию целевой функции, соответствующую С=0 – прямую 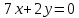 (на рисунке красная прямая, проходящая через начало координат) (на рисунке красная прямая, проходящая через начало координат)Требуется найти максимальное значение функции F на множестве D, сдвигаем линию уровня параллельно себе в направлении градиента- до тех пор, пока она не пройдет через последнюю точку многоугольника. Этой точкой будет А. Точка пересечения прямых 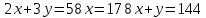 Найдем координату точки 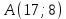 Получим 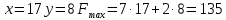 №8 Транспортная задача
Проверим необходимое и достаточное условие разрешимости задачи. ∑a = 180+300+120=600 ∑b = 110+350+140=600 Условие баланса соблюдается. Задача разрешима Найдем опорный план задачи методом северно-западного угла
Проверяем полученный опорный план на оптимальность. Для этого находим потенциалы пунктов отправления и назначения. Для заполненных клеток составляем систему из 5 уравнений с 6 неизвестными: 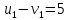 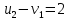 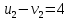 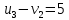 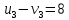 Полагая 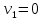 находим находим 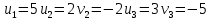 Для каждой свободной клетки вычисляем число 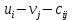
Среди полученных чисел есть положительные. Значит данный план не является оптимальным Максимальное положительное число 6 Пересчитываем план
Получили новый опорный план
Проверяем полученный опорный план на оптимальность. Для этого находим потенциалы пунктов отправления и назначения. Для заполненных клеток составляем систему из 5 уравнений с 6 неизвестными: 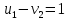 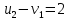 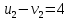 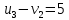 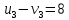 Полагая 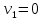 находим находим 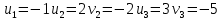 Для каждой свободной клетки вычисляем число 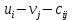
Среди полученных чисел есть положительные. Значит данный план не является оптимальным Максимальное положительное число 4 Пересчитываем план
Получили новый опорный план
Проверяем полученный опорный план на оптимальность. Для этого находим потенциалы пунктов отправления и назначения. Для заполненных клеток составляем систему из 5 уравнений с 6 неизвестными: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
