Решение было получено и оформлено с помощью сервиса Умножение матриц онлайн Вместе с этой задачей решают также
 Скачать 9.53 Kb. Скачать 9.53 Kb.
|
|
Матрица A 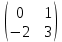 Матрица B 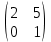 Вычисляем элемент новой матрицы (1,1): работаем с 1-ой строкой и с 1-м столбцом. 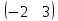 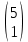 Получаем: 0∙2+1∙0 = 0 Вычисляем элемент новой матрицы (1,2): работаем с 1-ой строкой и с 2-м столбцом. 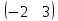 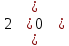 Получаем: 0∙5+1∙1 = 1 Вычисляем элемент новой матрицы (2,1): работаем с 2-ой строкой и с 1-м столбцом. 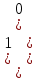 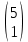 Получаем: (-2)∙2+3∙0 = -4 Вычисляем элемент новой матрицы (2,2): работаем с 2-ой строкой и с 2-м столбцом. 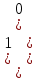 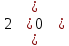 Получаем: (-2)∙5+3∙1 = -7 В итоге получаем матрицу AxB 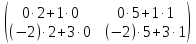 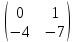 Решение было получено и оформлено с помощью сервиса: Умножение матриц онлайн Вместе с этой задачей решают также: Обратная матрица через алгебраические дополнения Координаты вектора в новом базисе Аналитическая геометрия и векторная алгебра Матричный калькулятор Решение матричных уравнений AX=B По координатам пирамиды найти: уравнение плоскостей, уравнение прямых |
