задачи для государственной аттестации. задачи госы. Решение цб может
 Скачать 0.58 Mb. Скачать 0.58 Mb.
|
|
Задача1. Объем денежной массы в стране составил на конец года 210 млрд руб. В начале года центральный банк произвел эмиссию в размере 6 млрд руб. и установил норму обязательных резервов 10%. Каков объем денежной массы в стране? Решение: Поскольку эмиссия происходит путем кредитования коммерческих банков, вся выпущенная сумма в размере 210 млрд ден. ед. осела на счетах в коммерческих банках. При условии, что безналичные деньги имеют способность к мультипликативному расширению, общая сумма денежных средств, представленная на денежном рынке коммерческими банками, составит 6 • 1/0,1 = 60 млрд ден. ед. Таким образом, денежная масса увеличится и составит 210 + 60 = = 270 млрд ден. ед. Ответ: 270 млдр ден.ед. Задача2. Экономика находится в условиях экономического бума. Денежная масса в обращении составляет 670 тыс. долл. Норма обязательных резервов 10%. Что должен сделать центральный банк, чтобы предотвратить надвигающийся кризис? Решение: ЦБ может: 1) Увеличить норму обязательных резервов (таким образом, снизится кредитная активность коммерческих банков и упадёт величина банковского мультипликатора, что призвано удержать рост предложения денег). На практике это выполняется не так часто, поскольку инструмент слишком мощный. 2) Продать государственные облигации на открытом рынке (тем самым, «изъять» у покупателей часть денежной массы). Задача3. Пусть общая сумма вкладов в коммерческий банк составляет 150 тыс., общая сумма резервов — 27 тыс. руб., а норма обязательных резервов — 10%. Ссуды какого размера могут выдать этот банк и вся банковская система в целом? Решение: Норма обязательных резервов = Rнорм.=Вклады в коммерческий банк* r = 150*0,1=15 тыс.руб. S одного банка = R – R норм. = 27-15=12 тыс.руб. S банковской системы = S1*1/r= 12*1/0,1=120 тыс.руб Ответ: 12 тыс руб, 120 тыс.руб Задача4. Пусть норма обязательных резервов равна 20%, бессрочные чековые вклады в банк составляют 800 тыс. руб., наличные деньги — 45 тыс. руб., резервные отчисления —90тыс. руб. Каковы избыточные резервы банка? Решение: 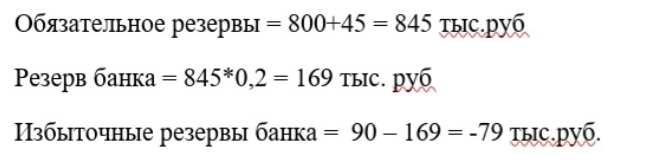 Задача5. Предположим, что в банк, у которого нет избыточных резервов, приходит вкладчик и приносит 1600 долл. наличными. Банк добавляет эти деньги к своим резервным отчислениям в центральный банк. После этого банк выдает ссуду в размере 1300 долл. Как изменится предложение денег? Решение:   Задача 6. Определить, под какую ставку процентов выгоднее поместить капитал в 10 000 000 руб. на 7 лет: под простую ставку процентов 12 % годовых; под сложную ставку процентов 5 % при ежеквартальном начислении? Решение: Достаточно найти, например, простую процентную ставку, эквивалентную данной сложной ставке, воспользовавшись формулой: r = ((1+0,05/4)28-1)/7 = ((1+0,0125)28-1)/7 = 0,42/7=0,06=6% Так как простая процентная ставка (6%), которая дала бы одинаковый с данной сложной процентной ставкой результат, значительно ниже предложенной (12%), ясно, что гораздо выгоднее использовать простую процентную ставку. Посчитаем теперь наращенные суммы, получаемые в обоих случаях, чтобы выяснить, насколько более выгодна простая ставка. S = 10 000 000*(1+7*0,12) = 18 400 000 руб. S = 10 000 000*(1+0,05/4)28=14 200 000 руб. Задача 7. Коммерческая организация планирует через два года приобрести помещения под склад. Эксперты оценивают будущую стоимость недвижимости в размере 12 млн. руб. По банковским депозитным счетам установлены ставки в размере 7 % с ежегодным начислением процентов и 4 % с ежеквартальным начислением процентов. Требуется: определить какую сумму необходимо поместить на банковский депозитный счет, чтобы через два года получить достаточную сумму для покупки недвижимости. Решение: 1 PV = 12 000 000 * (1/(1+0,07)2) = 12 000 000*(1/1,1449)=12 000 000*0,87=10 440 000 руб – более выгодным для предприятия является вложение меньшей суммы средств. 2 PV = 12 000 000 * (1/(1+0,04/4)2*4)=12 000 000 *(1/1,08) = 12 000 000* 0,93 = 11 160 000 руб Ответ: 1 вариант более выгодный Задача 8. Предприниматель может получить ссуду: а) либо на условиях ежемесячного начисления процентов из расчета 6 % годовых, б) либо на условиях полугодового начисления процентов из расчета 4 % годовых. Какой вариант более предпочтителен? Решение: А) Re = (1+0,06/12)12-1=1,06-1=0,06=6% Б) Re = (1+0,04/2)2-1=1,0404-1=0,0404=4,04% Ответ: второй вариант является более предпочтительным для предприятия. Задача 9. Первоначальные инвестиции (C0) в инвестиционный проект с ожидаемым сроком окупаемости 3 года составили 30 млн. руб. при ставке дисконта 15%. Темп инфляции 8%:
Определите, с учетом инфляции, чистую приведенную стоимость проекта NPV и сделайте вывод о возможной его реализации. Решение: Процентная ставка будет рассчитываться следующим образом: R = (1 + r) × K, где R – итоговая дисконтная ставка с учетом инфляции. r – показатель дисконта; K – уровень инфляции. R = (1+0,15)*0,08 = 0,092 = 9,2% NPV = -30 000 000 + (10 000 000/(1+0,092)1+(10 000 000/(1+0,092)2+(12 000 000/(1+0,092)3 = - 3 208 360,27 руб., так как NPV – меньше нуля, то данный проект не следует принимать . Задача 10. На основе нижеприведенных данных рассчитать себестоимость товарной продукции, затраты на 1 руб. товарной продукции и выявить факторы, влияющие на изменение затрат. Письменно сформулировать выводы. Таблица Расчет себестоимости товарной продукции
Вывод: Показатель затрат на 1 рубль продукции показывает соотношение полной себестоимости к выручке. Чем ниже показатель, тем лучше, тем больше прибыль. Если значение показателя стремится к 1, значит, прибыль организации стремится к нулю. Наибольший удельный вес в затратах занимают прочие затраты и амортизация основных фондов. Задача 11. Себестоимость товарной продукции в отчетном году составила 760 тыс. руб. Затраты на 1 руб. товарной продукции - 0,9 руб. В будущем году предполагается увеличить объем реализации продукции на 10%. Затраты на 1 руб. товарной продукции установлены на уровне 0,75 руб. Определите себестоимость товарной продукции будущего года. Решение: 1 Объем товарной продукции в отчетном году: 760 000/ 0,9=844 444 руб. 2 Увеличение объема товарной продукции на 10% составит в будущем году: 844 444*0,1=84 444,4 руб. 3 Объем товарной продукции будущего года составит: 844 444+84 444,4 = 928 888,4 руб 4 Себестоимость товарной продукции: 928 888,4 *0,75 = 696 666,3 руб. Ответ: 696 666,3 руб. Задача 12. В отчетном году себестоимость товарной продукции составила 550 800 руб., что определило затраты на 1 руб. товарной продукции – 0,89. В плановом году затраты на 1 руб. товарной продукции установлены в 0,85 руб. Объем производства и реализации продукции будет увеличен на 11%. Необходимо определить себестоимость товарной продукции планового года. Решение: Исходя из формулы затрат на 1 руб. товарной продукции: З=Sтп/Vтп, где Sтп – общая сумма затрат на производство (себестоимость) V тп – объем товарной продукции Объем товарной продукции в отчетном году: 550 800/0,89 = 618 876 руб. Объем товарной продукции планового года увеличился на 11% и составит: 1,11* объем товарной продукции отчетного периода =1,11*618 876 = 686 952 руб. Себестоимость товарной продукции в плановом году: 686 952*0,85 = 583 909,2 руб. Ответ: 583 909,2 руб себестоимость планового года. Задача 13. Определите себестоимость продукции на основании следующих данных: Таблица: Расчет полной себестоимости продукции
Решение:  Постоянные расходы на каждую продукцию: А = 1000/(1000+1500+2000)*90000 = 20 000 руб. Б = 1500/(1000+1500+2000)*90000=30 000 руб. В = 2000/(1000+1500+2000)*90000=40 000 руб. Себестоимость на ед.продукции: постоянные затраты/объем * переменные затраты А = 20000/1000*25 = 500 Б = 30000/1500*35=700 B = 40000/2000*40=800 Себестоимость на продукцию в общем: А = 500*1000 = 500 000 руб Б = 700*1500=1 050 000 руб В = 800*2000 = 1 600 000 руб. Итого: 500 000+1 050 000+1 600 000 =3 150 000 руб Ответ: 3 150 000руб Задача 14. В течение месяца предприятие приобрело для производственных нужд: ткань мебельную на сумму 94 940 руб., поролон – 50 600 руб., столярный станок – 52 960 руб., а также реализовало готовую продукцию на сумму 600 000 руб. и излишек материалов на сумму 30 240 руб. Указанная стоимость включает НДС по ставке 18%. Составить бухгалтерские проводки для указанных операций, определить сумму НДС для перечисления в бюджет.  Задача 15. Сотрудник организации – участник боевых действий в Афганистане, Герой России имеющий одного иждивенца получает по месту основной работы оклад в сумме 25000руб.Определить облагаемый налогом совокупный ежемесячный доход. Решение:  Задача 16. Гражданин в 2018 г. продал квартиру, которая принадлежала ему на праве собственности с 2016 г., за 2 500 000 руб. Определить какую сумму имущественного вычета может получить гражданин. Решение: Суть имущественного вычета по НДФЛ в том, что доходы налогоплательщика, которые следует облагать по ставке 13%, можно снизить на сумму такого вычета. Однако законодательством установлен верхний предел сумм, которые можно вычитать из дохода при продаже жилой недвижимости. Согласно подп. 1 п. 2 ст. 220 НК РФ размер такого вычета не может превышать 1 000 000 руб. Задача 17. Начисленная сумма по оплате труда за январь составила 34 000 руб. Рассчитайте суммы авансовых платежей за месяц в Пенсионный фонд РФ (бюджет) и в фонды социального и обязательного медицинского страхования. Решение: Сумма страховых взносов на пенсионное страхование: 34 000*0,22=7 480 Сумма страховых взносов на обязательное медицинское страхование: 34 000* 0,051=1 734 Сумма страховых взносов на обязательное социальное страхование: 34 000*0,029=986 Сумма страховых взносов на страхование от несчастных случаев на производстве и профзаболеваний: 34 000*0,002=68 Задача 18. Малое предприятие за I квартал выплатило в пользу штатных работников – заработную плату в размере 530 000 руб., премию по итогам работы за год – 56 000 руб., сумму по больничным листам – 30 500 руб., а также 15400 руб. по договорам подряда. Определите сумму начисленных за квартал страховых взносов. Решение: Налоговая база = 530 000+56 000+ 30 500+15 400 = 631 900 руб Сумма страховых взносов на пенсионное страхование = 631 900 *0,22 = 139 018 руб. Сумма страховых взносов на обязательное медицинское страхование = 631 900*0,051= 32 226,9 руб. Сумма страховых взносов на обязательное социальное страхование: 631 900*0,029 = 18 325,1 руб. Сумма страховых взносов на страхование от несчастных случаев на производстве и профзаболеваний: 631 900 *0,002 = 1 263,8 руб. Задача 19. По итогам 2018г. налогоплательщиком получены доходы 550 тыс. руб., понесены расходы в сумме 460 тыс. руб. Рассчитать сумму единого налога. Объект налогообложения – доход, уменьшенный на величину расходов. Решение: (550000-460000)*15%=13500 Ответ: 13500 руб. Задача 20. Банк выпустил 1 тысячу дисконтных облигаций номиналом 10 тыс. руб. и разместил их по цене 9800 руб. Определите расходы банка по привлечению дополнительного капитала. Решение: Дисконт по продаже 1 облигации = 10 000-9800 = 200 руб. Плата за привлечение дополнительного капитала: 200*1000 = 200 000 руб. Ставка дисконта: 200/9800*100 = 2,04% Задача 21 Депозит в размере 600 тыс.руб.положен в банк на полгода по ставке 7.8%годовых. Определите сумму начисленных процентов при условии их ежемесячного начисления. Решение: 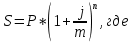 P – первоначальная сумма вклада J – номинальная ставка процентов m – число начисленных процентов за год n – число лет 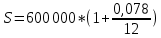 ^6 = 600 000 *1,04 =624 000 руб. – наращенная сумма ^6 = 600 000 *1,04 =624 000 руб. – наращенная сумма624 000 – 600 000 = 24 000 руб – сумма начисленных процентов за пол года. Ответ: 24 000 руб. Задача 22 Банк выдал кредит 10 млн. руб. на 2 года по сложной годовой ставке 18% годовых с погашением единовременным платежом. Определить погашаемую сумму и сумму начисленных процентов. Решение: Общая сумма погашения кредита : S = 10 000 000* (1+0,18)2 = 13 924 000 руб Сумма выплаченных процентов: I = 13 924 000 – 10 000 000 = 3 924 000 руб. Задача 23 Вексель на сумму 500 тыс. руб. предъявлен в банк за полгода до его погашения. Банк для определения своего дохода использует учетную ставку, равную 10% годовых. Определить сумму, выплаченную владельцу векселя, и сумму дохода (дисконта), полученного банком. Решение: Учет векселя: P=S*(1- n*d): где: Р - выплачиваемая сумма по векселю, S - сумма векселя, п - количество периодов наращивания, d - учетная ставка. Учет векселя: 500 000 * (1 – 0,5*0,1) = 475 000 руб. Сумма дисконта (дохода) банка: 500 000 – 475 000 = 25 000 руб. Задача 24 Рассчитайте коэффициент ипотечной задолженности, если стоимость недвижимости 2 млн. руб., а сумма ипотечного кредита 1800 тыс. руб. Решение: Коэффициент ипотечной задолженности = 1 800 000/ 2 000 000 * 100% = 90% Ответ: 90% Задача 25 Определите рентабельность деятельности коммерческого банка, уставный фонд которого 100 млн. руб. Доходы за год – 70млн. руб., расходы – 50 млн. руб. Решение: Коэффициент общей рентабельности (Ро) определяется как отношение прибыли к совокупному расходу Р0=П/Р Прибыль = доходы – расходы = 70-50=20 млн руб. Коэффициент общей рентабельности деятельности коммерческого банка = 20/50=0,4 Рентабельность собственного капитала = прибыль/ собственный капитал *100% = 20/100*100%=20% Ответ: 0,4 Коэффициент общей рентабельности характеризует величину прибыли, приходящейся на 1 рубль совокупных расходов. Это один из основных показателей, определяющих эффективность банковской деятельности. Нормативного значения не имеет. Задача 26 Если автомобиль стоит 5000 евро, сколько Вам нужно долларов для его покупки? Прямым или обратным курсом Вы воспользуетесь для расчетов? Решение: 5000*0,9105 (стоимость 1 евро к доллару)=4552,5 (обратная котировка) Ответ: 4552,5 Задача 27. Определить объем производства и продаж, если имеются следующие данные: постоянные затраты предприятия FC = 650 тыс. руб. в год; переменные затраты VC = 50 руб. на единицу продукции. Цена единицы продукции – 200 руб. Определить объем производства и продаж, при котором прибыль составит- 300 тыс. руб. Какая будет прибыль предприятия, если объем продаж снизится на 15 % Решение:
Прибыль = Выручка – Переменные затраты – Постоянные затраты Выручка = (Цена единицы продукции) * (Объем производства); Переменные затраты = (Удельные переменные затраты) * (Объем производства); Объем производства = (Прибыль + Постоянные затраты)/(Цена единицы продукции – Удельные переменные затраты). Объем производства=650 000+300 000 / (200-50)=6 334 Выручка = 200*6334=1 266 800 Переменные затраты: 50*6334=316 700 Воздействие изменения объема продаж на прибыль оценивают при помощи эффекта операционного рычага рассчитываемого как отношение маржинального дохода к прибыли: СВОР = (Выручка – Переменные затраты)/Прибыль; СВОР = (1266800 – 316700)/300000 = 3,2 Таким образом, при изменении объема продаж на 1% прибыль изменится на 3,2%. Объем продаж снизился на 15%: 1266800∙(1-0,15)=1076780; объем производства составит 6334∙(1 - 0,15) = 5383,9, следовательно, прибыль изменится следующим образом: 15%∙3,2 = 48%, 300000∙(1-0,48) = 156000.
Ответ: объем производства = 6334 тыс руб, прибыль = 156 000 руб, объем продаж = 1266800 руб. Задача 28. Первоначальные инвестиции в новое оборудование I0 =2300 тыс. руб. Ожидаемый чистый денежный поток NCF = 700 тыс. руб. Срок службы оборудования - 5 лет. Норма дисконта 10%. Оправданы ли затраты на приобретение нового оборудования? Решение: NPV = -2 300 000 + 700000/(1+0,1)1+700 000/(1+0,1)2+700 000/(1+0,1)3+700 000/(1+0,1)4+700 000/(1+0,1)5 = - 81094,16 руб. – данные затраты на приобретение нового оборудования не оправданы. Задача 29. Определите средневзвешенную стоимость капитала, если организация планирует сохранять действующую структуру капитала в следующем соотношении: - собственный капитал – 50%; - нераспределенная прибыль – 10%; - заемный капитал (кредит) – 40%. Известно, что стоимость привлечения собственного капитала 20%, стоимость привлечения заемных источников финансирования 14% годовых, ставка налога на прибыль 20%. Решение: 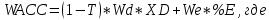 Wd – стоимость привлеченных заемных источников финансирования XD – заемный капитал We – (собственный капитал + нераспределенная прибыль) %E – стоимость привлечения собственного капитала WACC = (1-0,2)*0,14*0,4+0,6*0,2 = 0,8*0,14*0,4+0,6*0,2 = 0,1648 = 16,48% Ответ: 16,48% Задача 30. Чистая прибыль ОАО составляет 20000 тыс. руб. Количество обыкновенных акций 1 млн. штук. Рыночная цена одной акции 20 руб. ОАО планирует направить 50% чистой прибыли на развитие производства. Определите прибыль на акцию, дивиденд на акцию и коэффициент выплаты дивиденда. Решение: Прибыль на акцию EPS= чистая прибыль/ число акций EPS= 20 000 000/1 000 000 = 20 руб. Сумма дивидендных выплат из нераспределенной прибыли составляет: 20 000 000*0,5 = 10 000 000 руб. Дивиденд на акцию DPS = сумма дивидендных выплат/число акций DPS = 10 000 000/ 1 000 000 = 10 руб. Коэффициент выплаты дивиденды DY = дивиденд на акцию(DPS) / рыночную цену DY = 10 руб /20 руб = 0,5 = 50% Задача 31. Определите эффект финансового рычага, возникающего при привлечении заёмного капитала в объёме 5000000 тыс. руб. под 20% годовых, величина собственного капитала составляет 9000000 тыс. руб. Экономическая рентабельность – 25%, ставка налога на прибыль – 20%. Решение: ЭФР = (1-0,2)*(ЭР-ССП)*ЗК/СК ЭФР= (1-0,2)*(0,25 – 0,2)*(5000000/9000000)=0,8*0,05*0,56=0,0224=2,24% Эффект рычага положительный – увеличение заемного капитала повышает рентабельность собственного капитала. Ответ: 2,24% Задача 32. Вкладчик разместил на 4 года в банке 40 тыс. руб. Начисляются сложные проценты: в первом году – по ставке 8 %, во втором 7 %, в третьем – 9 %, в четвертом – 7%. Определить будущую стоимость вклада к концу четвертого года. Решение: SUM=x*(1+%) 1 год = 40 000*(1+0,08) = 43 200 2 год = 43 200*(1+0,07) = 46 224 3 год = 46 224*(1+0,09)=50 384,16 4 год = 50 384,16*(1+0,07) =53 911,05 руб. Ответ: 53 911,05 руб. Задача 33. Определить текущую стоимость долга, если Вам должны вернуть 100 тыс. руб. через 2 года, но должник готов сегодня погасить долг из расчета 12% годовых. Решение: FV будущая стоимость долга = 100 000 руб N = 2 года I = 12% PV текущая стоимость долга = 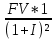 PV = 100 000* 1/(1+0,12)2 = 79 719,4руб. Ответ: текущая стоимость долга = 79 719,4 руб. Задача 34. Среднерыночная доходность акции составляет 17 %, безрисковая ставка – 12 %. По акции А доходность составляет 20 %, а β -коэффициент 1,2. При таких условиях акция А переоценена или недооценена? Решение: Цена акции определяется по формуле: Ra=Rf+β*(Rd-Rf), где Ra - цена акции Rf – доходность безрисковых ценных бумаг β - бэта – коэффициент Rd - доходность среднерыночных ценных бумаг Ra = 12+1,2*(17-12) = 18% меньше доходности по акции А(20%) следовательно акция недооценена. Ответ: акция недооценена. Задача 35. Определите выгодность вложений 1000 тыс. руб. при ставке дисконта 10% годовых под простые и сложные проценты (проценты по вкладу начисляются 1 раз в конце срока вклада): 1. На срок 6 мес. 2. На срок 1 год. 3. На срок 2 года.  Задача 36. Предприятие инвестирует 3 млн. руб. в новое оборудование. Ожидаемые поступления чистого денежного потокa NCF = 1 млн. руб. Срок службы 6 лет. Ставка дисконтирования 10 %. Является ли данный проект приемлемым? Решение: NPV = - 3 000 000 + (1 000 000/1+0,1)1+(1 000 000 /1+0,1)2+(1 000 000 /1+0,1)3+(1 000 000 /1+0,1)4+(1 000 000 /1+0,1)5+(1 000 000 /1+0,1)6= - 3 000 000 +909 090,9 + 826 446+751 314,8+683 013,5+620 921+564 474 = - 3 000 000 + 4 355 260,2 = 1 355 260, 2 руб, так как NPV больше 0, следовательно затраты оправданы и данный проект приемлемый. Задача 37. Рыночная цена обыкновенных акций предприятия составляет 1000 руб. Ожидается, что их рыночная цена за 2 года вырастет до 1200 руб. Предполагается, что на каждую акцию в конце следующих 2 лет будет выплачено по 100 руб. дивидендов. Определите текущую (внутреннюю) стоимость акции и её доходность; оцените привлекательность акции как формы вложения денежных средств, если требуемая доходность составляет 12%. Решение: дивиденд выплачивается только в конце второго года, если следовать условиям задачи текущая стоимость акции: 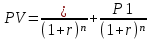 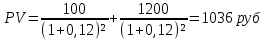 Так как текущая стоимость акции выше рыночной стоимости акции – рекомендуется эти акции купить, так как они недооценены. Найдем годовую доходность: 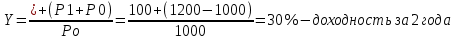 Найдем ориентировочную годовую доходность: 30%:2 = 15% - ориентировочная годовая доходность Ответ: 1036 руб, 15% Задача 38. Бескупонная облигация со сроком обращения полгода, приобретена на аукционе за 68% от цены, а потом была продана за 78%. Доходность по аукциону, по результатам сделки, оказалась в 2 раза меньше доходности к погашению. Рассчитать через сколько дней после аукциона была продана облигация. Решение: R=(100-68)/68/180*365*100=95.42 R аук= 47,71=(78-68)/68/X*365*100 47.71/36500=0.147/X X=113 дней Ответ: 113 дней Задача 39. Бескупонная облигация куплена за 200 дней, а продана за 165 дней до своего погашения. В момент покупки процентная ставка на рынке – 110% годовых, а момент продажи – 90% годовых. Рассчитать доходность от операций купли-продажи в виде годовых процентов. Решение: Пусть П1 = цена покупки(110) , П2 =цена продажи (90%) Т1= срок до погашения при покупке (200) , Т2= срок погашения при продажи (165) I = (P2-P1\P1)*B\b*100 B – дней в году b- срок обращения ( Т2- Т1) Доходность облигаций по ф-ле (D1= 110 d2 = 90 ) Д =(N\P-1)*B\T*100 P = N\D*T I =(d1*t1-d2*t2)\(d2*t2+B*100)* B\(t1-t2)* 100 = 145% Задача 40 ОАО по итогам года получило чистую прибыль в размере 500 млн. руб. Уставный капитал общества составляет 2 млн. руб. Все акции имеют единый номинал – 10 руб. Общее собрание акционеров приняло решение о выплате дивидендов по обыкновенным акциям в размере 20 руб. на одну акцию. Рассчитайте размер дивиденда на одну привилегированную акций с правом участия, если на выплату дивидендов по ним направляется 12% чистой прибыли ежегодно. Уставный капитал общества на 87% состоит из обыкновенных акций. Решение: Так как уставный капитал общества на 87% состоит из обыкновенных акций, найдем стоимость уставного капитала: 2 000 000*87 : 100 = 1 740 000 руб. - обыкновенные акции Тогда уставный капитал общества привилегированных акций будет составлять 13% (100 - 87). 2 000 000*13 : 100 = 260 000 руб. - привилегированные акции. Номинал акции рассчитывается: Нак = Уставный капитал : Количество акций Отсюда найдем количество обыкновенных акций: 1 740 000 : 10 = 174 000 штук Найдем количество привилегированных акций: 260 000 : 10 =26 000 штук Найдем чистую прибыль, направленную на выплату дивидендов по привилегированным акциям: Чп пр = 500 000 000 * 12% : 100% = 60 000 000 руб. Дивиденд = Чистая прибыль общества, которая полностью была выплачена в виде дивидендов / количество акций Д пр = 60 000 000 / 26 000 = 2308 руб Цена 1-ой привилегированной акции = 2308/ 10=230,8 руб. Ответ: 230,8 руб Задача 41 Определите доходность к погашению ГКО, если известно, что по результатам торгов средневзвешенная цена составила 94%, цена последней сделки – 95, до погашения осталось 80 дней. Решение: При расчете на основе цены последней сделки: 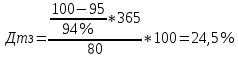 При расчете по средневзвешенной: 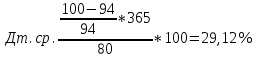 Ответ: в данном случае при расчете по средневзвешенной цене доходность получается значительно больше (5% при сроке 80 дней погашения). Задача 42 Текущая доходность привилегированных акций составляет 9%. Номинальная стоимость акций составляет 12000 руб. дивиденд объявлен в размере 12%. Определите рыночную цену акций. Решение: Обозначения, принятые в задаче: N = 12 000 руб. - номинальная стоимость акции; q = 12% - объявленный дивиденд привилегированной акции; dг = 9% - текущая доходность; X = рыночная цена акции (неизвестна). Приведенные в условии задачи величины связаны между собой соотношением dг = qN/X. Можно определить рыночную цену привилегированной акции: X = qN/dг =0,12*12 000 / 0,09= 16 000 руб Ответ: Таким образом, описанная в условиях задачи ситуация корректна при условии, что рыночная цена привилегированной акции составляет 16 000 руб. Задача 43 Коммерческим банком выдан вексель на 120 тыс.рублей со сроком погашения через 8 месяцев. Какую сумму внес в банк владелец векселя, если доходность по векселям такой срочности в банке составляет 20% годовых? Решение: 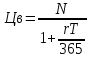 Цв = 120 000/(1+0,2*240)/365 = 15 600 руб. Ответ: 15 600 руб. Задача 44. Страховая оценка объекта страхования в2014 году равна 10000 рублей. Договор страхования заключен на страховую сумму 8 000 рублей. Ущерб составил 4 000 рублей. Определить сумму страхового возмещения. Решение: В данном случае страховая оценка объекта страхования равна страховой сумме, поэтому сумма страхового возмещения равна сумме ущерба. Q = T*(S/W), где Q – сумма страхового возмещения T – страховой ущерб S – страховая сумма W – страховая оценка Q = 4000*(8000/10000) = 3200 руб Ответ: 3200 руб. Задача 45. Страховая оценка объекта страхования составляет 980 000 рублей. Договор страхования заключен на страховую сумму 60 0000 рублей. Ущерб составил 30%. Определить сумму страхового возмещения. Решение: Q = T*(S/W) T – 30% S – 60 000 руб W – 980 000 руб Q - ? Чтобы найти ущерб: х -30% 980 000 – 100% Х = 294 000 руб – ущерб Q = 294 000*(60 000 / 980 000) =18000руб. Ответ: страховое возмещение равно 18000 руб. Задача 46. Определить требуемую первоначальную денежную сумму, отданную в кредит, если через 5 лет страховой фонд составил 250 000 рублей. Решение: n = 5 – время, в течении которого сумма находится в обороте i = 3% - норма доходности (процентная ставка) Bn = 25 000 – денежная сумма через n лет А = ? – первоначальная денежная сумма Первоначальная денежная сумма, отданная в кредит на n лет определяется по формуле: А = Bn × 1/(1+i)n = Bn × Vn Vn определяем по таблице дисконтирующего множителя А = 25 000 × 0,86261 = 21 565,25 рублей Ответ: первоначальная денежная сумма 21 565,25 рублей Задача 47. Необходимо через 5 лет иметь страховой фонд в размере 1000 000 рублей. Определить современную стоимость страхового фонда (при норме доходности 3%). Решение: А = Bn*Vn Bn – 1 000 000 руб Vn = 1/(1+i)n = 1/(1+0,03)5=0,86 A = 1 000 000*0,86=860 000 руб – современная стоимость страхового фонда Ответ: 860 000 руб. Задача 48. Определить, во что превратится денежная сумма величиной в 100 000 рублей через 10 лет, отданная в кредит при норме доходности 8%. Решение: Денежная сумма, отданная в кредит через n лет, определяется по формуле: Bn = A*(1+i)n, где А – первоначальная денежная сумма, отданная в кредит i - норма доходности Bn = 100 000 *(1+0,08)10 = 100 000 *2,16 = 216 000 руб. Ответ: 216 000 руб. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
